Описание случайных погрешностей и их числовая оценка

Конкретное значение случайной погрешности предсказать невозможно.

Но совокупность случайных погрешностей измерения подчиняется статистиче­ским закономерностям.

Это обстоятельство позволяет применять к изучению и описанию случайных погрешностей измерения методы теории вероятностей и математической статистики.

В вероятностной модели случайные погрешности ΔХ и сами результаты измерения рассматриваются как непрерывные случайные величины, которые могут принимать любые действительные значения.

Причем каждому интервалу (x1...x2) соответствует вполне определенное число, называемое ве­роятностью попадания значения случайной величины X в этот интервал и обо­значаемое:

P(x1<X<x2)

Находить эти вероятности можно на основе закона распределения вероятностей случайной величины X. Чаще всего принимают x1 = - ∞.

Тогда, обозначив x2 = х, имеем:

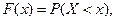
где F(х) —интегральная функция распределения:

р(х)—некоторая неотрицательная функция, называемая плотностью распре­деления и подчиняющаяся условию:

При решении большинства практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероят­ности. Удобнее пользоваться некоторыми количественными показателями, ко­торые дают в сжатой форме достаточную информацию о случайной величине.

Такие показатели называют числовыми характеристиками случайной величи­ны. Основными из них являются:

· математическое ожидание М(Х);

· мода (Мо);

· ме­диана (Ме);

· дисперсия D(X).

Для непрерывной случайной величины X, возможные значения которой принадлежат интервалу {х1...x2), математическое ожидание:

Модой Mo непрерывной случайной величины называют такое ее значение X, при котором плотность распределения р(х) имеет максимум.

Медиана Me непрерывной случайной величины — такое ее значение X, при котором равновероятно, что случайная величина окажется меньше или больше медианы, то есть справедливо равенство:

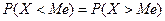
Если распре­деление одномодальное и симметричное, то математическое ожидание, мода и медиана совпадают.

Дисперсия является характеристикой рассеяния случайной величины отно­сительно ее математического ожидания:

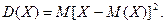
При оценке рассеивания удобнее пользоваться средним квадратическим отклонением:

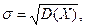
которое называют также стандартным отклонением или стандартом.

Диспер­сию можно представить в виде:

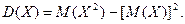
Случайные погрешности измерения чаще всего подчиняются закону нор­мального распределения (закону Гаусса).

Рис.8.5. – Функция нормального распределения

Функция плотности распределения в данном случае имеет вид:

где параметр σ характеризует точность измерений.

При расчетах широко при­меняется нормированное нормальное распределение, которое получается при переходе к случайной величине

;

.

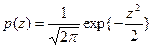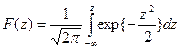Для нахождения F(z) применяют таблицы значений функции Лапласа
Ф(z), определяемой выражением:

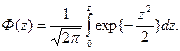
При z>0: а при z<0: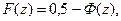

Распределение Максвелла (Рэлея ) случайной величины, принимающей только неотрицательные значения (X и У — случайные коорди­наты точки, распределенные независимо и нормально), характеризует такие погрешности, как эксцентриситет, несоосность, биение, разностенность, непарал­лельность или неперпендикулярность.

Рис. 8.6. – Функция распределения Максвелла

Если в качестве нормированной перемен­ной принять 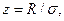где σ — стандартное отклонение параметра R, то функ­ция плотности распределения Максвелла:

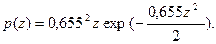
Равномерное распределение свойственно погрешностям округления до бли­жайшего деления шкалы прибора, а также погрешностям, соизмеримым с от­счетом.

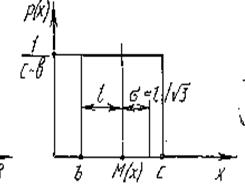
Рис.8.7. – Функция равномерного распределения

В данном случае функция плотности распределения имеет вид:

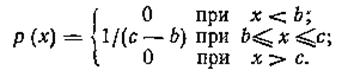
Дата добавления: 2014-12-27