Числовая оценка случайных погрешностей

Совокупность всех возможных значений исследуемой случайной погреш­ности называется генеральной совокупностью.

Множество значений случайной погрешности, полученное в результате наблюдения над нею, называют случай­ной выборкой или просто выборкой.

Число объектов в генеральной совокупно­сти и в выборке характеризует их объем. Генеральная совокупность может иметь бесконечный объем.

Основной задачей является получение научно обоснованных выводов о числовых характеристиках генеральной совокупности случайных погрешностей по выборке.

Выборочная оценка должна обладать следующими свойствами:

· не­смещенностью;

· эффективностью;

· состоятельностью.

Оценку А параметра А называют несмещенной, если ее математическое ожидание равно оцениваемому параметру.

Требование несмещенности гаран­тирует отсутствие систематических ошибок при оценке параметров.

Так как А — случайная величина, значение которой изменяется от выборки к выбор­ке, то меру ее рассеивания характеризуют дисперсией D(A). Из двух оценок А следует отдать предпочтение той, которая обладает меньшим рассеиванием (т. е. меньшей дисперсией).

Несмещенную оценку А которая имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра А, вычисленных по выборкам од­ного и того же объема, называют эффективной оценкой.

Оценку А параметра А называют состоятельной, если при неограниченном увеличении объема выборки ее значение приближается сколь угодно близко к значению оцениваемого параметра.

На практике не всегда удается удовлетворить одновременно требованиям несмещенности, эффективности и состоятельности оценки параметра.

Иногда для простоты расчетов целесообразно использовать незначительно смещенную оценку.

Оценку неизвестного параметра генеральной совокупности одним числом называют точечной оценкой.

Точечной оценкой математического ожидания М(Х) случайной величины X является среднее арифметическое значение X, вычисленное по результатам m независимых наблюдений:

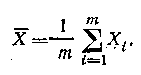
Эта оценка является несмещенной, состоятельной и эффективной. Она име­ет дисперсию σ2/m, если дисперсия случайной величины X равна σ2.

Несмещенной оценкой дисперсии генеральной совокупности D(X) являет­ся исправленная выборочная дисперсия:

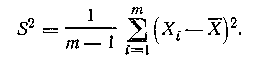
Эта оценка является состоятельной, но не эффективной.

При малом числе наблюдений необходимо использовать интервальное оценивание, так как в этом случае точечная оценка недостаточно надежна.

Не­обходимо по данным выборки построить числовой интервал, в котором с зара­нее выбранной вероятностью находится значение оцениваемого параметра.

Доверительным интервалом (А 2— А 1) для параметра А называют такой ин­тервал, для которого с заранее выбранной вероятностью Р=1 — α, близкой к единице, можно утверждать, что:

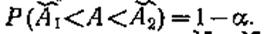
Чем меньше для выбранной вероятности (А 2— А 1), тем точнее оценка па­раметра А.

Доверительный интервал меняется от выборки к выборке.

Вероятность Р=1 — α называется доверительной вероятностью, а число α — уровнем значимости.

Выбор доверительной вероятности зависит от кон­кретной решаемой задачи.

Если случайная величина распределена нормально, а дисперсия этого рас­пределения неизвестна, то доверительный интервал для математического ожи­дания М(Х) определяется неравенством:

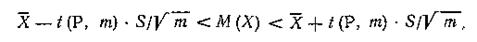
где t(P, m) —критерий Стьюдента, выбираемый их соответствующей таблицы, при доверительной вероятно­сти Р и числе степеней свободы f = m—l.

Если случайная величина распределена нормально, доверительный интер­вал для дисперсии генеральной совокупности при доверительной вероятности Р=1 — α определяется неравенством:

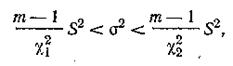
где χ2 — критерий Пирсона, выбираемый из соответствующей таблицы, который соответствует дове­рительной вероятности, равной 0,5α, для 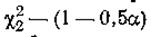; определяется при .

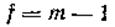Дата добавления: 2014-12-27