Объединение результатов неравноточных измерений

Одну и ту же величину часто измеряют различными приборами, в разных лабораториях или разные операторы.

Иногда возникает задача объединения по­лученных данных для того, чтобы получить наиболее точную оценку измеряемой величины.

Пусть имеется n групп измерений одной и той же величины А с соответствующими оценками измеряемой величины Х 1, Х2,..., Хn, причем

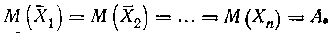
Известны оценки дисперсии и число наблюдений в каждой группе m1, m2,..., mn.

Оценка А по дан­ным всех измерений:

где

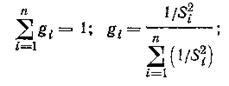
gi — вес i-й серии наблюдений.

Дисперсия, характеризующая точность оценки величины A определяется по формуле:

Погрешность определения веса любой серии наблюдений практически не отражается на точности объединенной оценки параметра А;

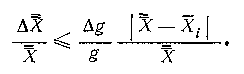
Второй сомножитель правой, части этого неравенства — порядка 0,01.

По­этому погрешность оценки среднего взвешенного из-за погрешности определе­ния весов будет не менее чем в 100 раз меньше последней.

В отдельных случаях можно пренебречь систематическими погрешностями измерения и предположить, что полученные оценки отличаются незначительно и обусловлены случайными погрешностями измерения.

Гипотеза о равенстве дисперсий в n группах измерений проверяется с по­мощью критерия Пирсона.

Наблюдаемое значение критерия:

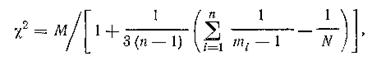
Где

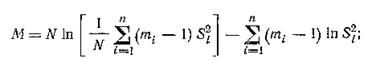
Для выбранной доверительной вероятности Р и числа степеней свободы f=n-1 критическое значение критерия Пирсона

Если , то гипотеза о равенстве дисперсий принимается.

Тогда вес i-й серии наблюдений следует определять как:

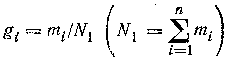
а дисперсию оценки параметра А - по формуле:

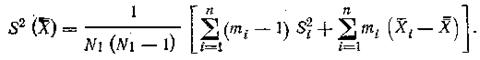
При измерении одной величины n приборами возможны ситуации, когда реальные погрешности измерения неизвестны, а известны только оценки границ погрешностей Δi (i=1, 2,..., n), объединяемых результатов измерений при за­данном значении доверительной вероятности Р.

Тогда доверительная погреш­ность оценки параметра А, если погрешности приборов имеют равномерное рас­пределение и Δш=Δ, будет:

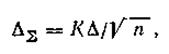
где К зависит от доверительной вероятности (может колебаться от 1,1 при Р=0,95 до 1,4 при Р=0,99).

Дата добавления: 2014-12-27