
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 18. Неопределенный интеграл и его свойства
|
|
|
|
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
План:
11. Понятие неопределенного интеграла.
12. Основные свойства неопределенного интеграла.
13. Таблица основных интегралов.
- Понятие неопределенного интеграла
Напомним, что основная задача дифференциального исчисления заключается в следующем: по данной функции f(x) требуется найти её производную. Для дифференцирования существует обратная операция: нахождение первоначальной функции F(x) по известной производной f(x). Эта операция получила название интегрирование (от лат. integratio – восстановление).
Так, попытаемся по известной производной 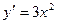 восстановить первоначальную функцию. Она будет иметь вид: y=х3. Обозначим известную функцию f(x) (в нашем примере f(x)=3х2), а первоначальную функцию F(x) (в нашем примере F(x)=х3). Функцию F(x) назовем первообразной данной функции f(x).
восстановить первоначальную функцию. Она будет иметь вид: y=х3. Обозначим известную функцию f(x) (в нашем примере f(x)=3х2), а первоначальную функцию F(x) (в нашем примере F(x)=х3). Функцию F(x) назовем первообразной данной функции f(x).
Функция F(x) называется первообразной для функции f(x) на интервале (а;b), если для всех x из этого промежутка справедливо равенство:
F'(x) = f(x), или, что то же самое, dF(x)= f(x)dx.
Пример 18.1. Найдите какую-либо первообразную для функции f(x)= 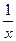 .
.
Решение. Функция F(x) = lnx является первообразной для f(x)= 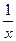 , т.к. F'(x)=(lnx) ' = =
, т.к. F'(x)=(lnx) ' = = 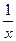 = f(x).
= f(x).
Нетрудно заметить, что первообразная lnx не является единственной для функции f(x)= 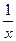 . В самом деле, в качестве первообразной можно было взять и функции lnx +3, lnx -7 и вообще lnx + С, где С - произвольная постоянная, потому что (lnx + С) ' =
. В самом деле, в качестве первообразной можно было взять и функции lnx +3, lnx -7 и вообще lnx + С, где С - произвольная постоянная, потому что (lnx + С) ' = 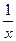 .
. 
Приведём формулировку теоремы, выражающей основное свойство первообразных.
Теорема 1. Если функция F(x) есть первообразная для функции f(x) на некотором промежутке (а;b), то множество всех первообразных для f(x) задается формулой: F(x) + C, где С – константа.
Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x) и обозначается символом 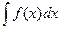 (читается: «интеграл от эф от икс де икс»).
(читается: «интеграл от эф от икс де икс»).
Таким образом, по определению 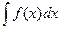 = F(x) + C.
= F(x) + C.
Функция f(x) называется подынтегральной функцией,
f(x)dx – подынтегральным выражением,
х - переменной интегрирования,
символ 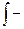 знаком неопределённого интеграла.
знаком неопределённого интеграла.
Пример 18.2. Найдите 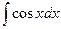 .
.
Решение. Т.к. cosx = (sinx) ', то функция F(x)= sinx является одной из первообразных для функции f(x) = cosx. Поэтому 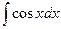 = sinx+С.
= sinx+С.
 Геометрически неопределённый интеграл представляет собой семейство кривых, каждая из которых получается из любой другой параллельным переносом вдоль оси Oy ( рис. 18.1). График каждой первообразной называется интегральной кривой.
Геометрически неопределённый интеграл представляет собой семейство кривых, каждая из которых получается из любой другой параллельным переносом вдоль оси Oy ( рис. 18.1). График каждой первообразной называется интегральной кривой.
Встает вопрос: для всякой ли функции существует неопределенный интеграл? Справедлива следующая теорема:
Теорема 2. Всякая непрерывная на (а;b) функция имеет на этом промежутке первообразную, а следовательно, и неопределённый интеграл.
- Основные свойства неопределенного интеграла
Отметим ряд свойств неопределенного интеграла, вытекающих непосредственно из определения.
1. Производная неопределённого интеграла равна подынтегральной функции: 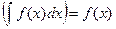 .
.
Докажем это свойство: 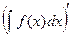 = (F(x) + C) ' = F'(x) = f(x).
= (F(x) + C) ' = F'(x) = f(x).
Благодаря данному свойству правильность интегрирования проверяют дифференцированием.
Пример 18.3. Докажите справедливость равенства: 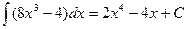 .
.
Решение. Воспользуемся свойством 1: найдем производную неопределенного интеграла. 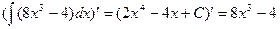 , что совпадает с подынтегральным выражением. Следовательно, интеграл
, что совпадает с подынтегральным выражением. Следовательно, интеграл 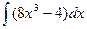 найден верно.
найден верно.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению: 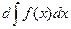 = d (F(x) + C) ' = F'(x) dx = f(x) dx.
= d (F(x) + C) ' = F'(x) dx = f(x) dx.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс константа С: 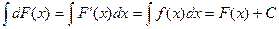 .
.
Рассмотрим ещё два свойства неопределённого интеграла, которые значительно расширяют возможности интегрирования.
4. Постоянный множитель можно выносить за знак интеграла, т.е. если k- const, k 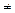 0, то
0, то
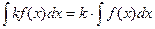 . (6)
. (6)
5. Неопределённый интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций:
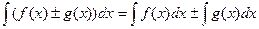 .
.
- Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть операция, обратная дифференцированию, можно получить следующую таблицу неопределенных интегралов:
1.  2.
2. 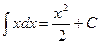 3.
3. 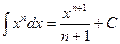 7.
7. 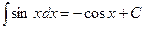 8.
8. 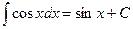 9.
9. 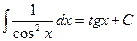 10.
10. 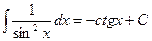 11.
11. 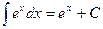 12.
12. 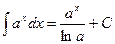 13.
13. 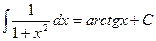
| 4. 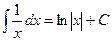 5.
5. 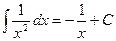 6.
6. 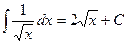 14.
14. 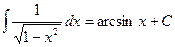 15.
15. 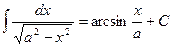 , а – const
16. , а – const
16. 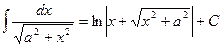 17.
17. 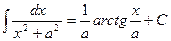 18.
18. 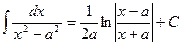 19.
19. 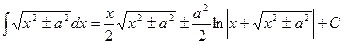
|
В справедливости этих формул, получивших название табличных интегралов, можно убедиться, как и в примере 18.3, с помощью дифференцирования. Производная правой части должна быть равна подынтегральной функции.
Контрольные вопросы:
- Какая операция является обратной для операции дифференцирования? В чем сущность этой операции?
- Что называют первообразной функции f(x)?
- Сколько у функции существует первообразных?
- Что называют неопределенным интегралом от функции f(x)?
- Каков геометрический смысл неопределенного интеграла?
- Перечислите основные свойства неопределенного интеграла.
- Как проверить правильность нахождения интеграла?
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 6540; Нарушение авторских прав?; Мы поможем в написании вашей работы!