
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определенного интеграла
|
|
|
|
Лекция 22. МЕТОДЫ ВЫЧИСЛЕНИЯ
План:
1. Применение формулы Ньютона-Лейбница.
2. Интегрирование подстановкой (заменой переменной).
3. Интегрирование по частям.
- Применение формулы Ньютона-Лейбница.
Простым и удобным методом вычисления определенного интеграла 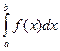 от непрерывной функции является формула Ньютона-Лейбница:
от непрерывной функции является формула Ньютона-Лейбница: 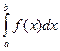 =
= 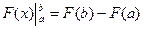 . Этот метод применяется во всех случаях, когда может быть найдена первообразная F(х) для подынтегральной функции f(х).
. Этот метод применяется во всех случаях, когда может быть найдена первообразная F(х) для подынтегральной функции f(х).
Пример 22.1. Вычислите  .
.
Решение. Сначала найдем неопределенный интеграл от заданной функции как интеграл от некоторой сложной функции, добавив границы интегрирования:  =
=  .
.
Подставим сначала верхнюю, потом нижнюю границы интегрирования:  = =
= = 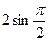 -
- 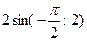 =
= 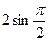 -
- 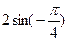 =
= 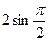 +
+ 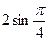 =2∙1+
=2∙1+ 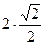 =
=  .
.
Ответ:  =
=  .
.
- Интегрирование подстановкой (заменой переменной).
При вычислении определенных интегралов широко используется метод замены переменной. Пусть требуется вычислить интеграл от сложной функции  . Как и для неопределенного интеграла, сделаем подстановку u=g(х). Тогда
. Как и для неопределенного интеграла, сделаем подстановку u=g(х). Тогда 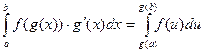 . Эта формула называется формулой замены переменной в определенном интеграле.
. Эта формула называется формулой замены переменной в определенном интеграле.
Алгоритм вычисления определенных интегралов методом замены переменной практически не отличается от алгоритма метода замены переменной для неопределенных интегралов (лекция 19). Отметим два принципиальных различия:
1. В определенном интеграле обязательной является смена границ интегрирования. Новая нижняя граница интегрирования будет равна u1 = g(а), а новая верхняя граница u2 = g(b).
2. При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется.
Рассмотрим применение метода замены переменной в определенном интеграле.
Пример 22.2. Вычислите  .
.
Решение. 1. Выполним подстановку u= 1 -cosx с целью прийти к интегралу от функции f(u) =  .
.
2. Найдем du по формуле du=и'dx: du=( 1 -cosx)'dx =sinxdx.
3. Выразим dx из выражения пункта 2 (du=sinxdx):  .
.
4. Подставим и и dx в исходный интеграл (пока неопределенный): 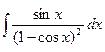 =
= 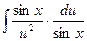 . Видим, что sinх можно сократить и прийти к интегралу относительно переменной и:
. Видим, что sinх можно сократить и прийти к интегралу относительно переменной и: 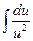 .
.
5. Вычислим новые границы интегрирования для переменной и. Для этого подставим существующие границы (π, 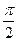 ) в выражение u= 1 -cosx.
) в выражение u= 1 -cosx.
Тогда нижняя граница u1 =1-  =1-0=1; верхняя граница u2 =1- cosπ= 1-(-1)=2.
=1-0=1; верхняя граница u2 =1- cosπ= 1-(-1)=2.
В результате всех преобразований первоначальный интеграл примет вид: 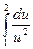 .
.
6. Вычислим полученный интеграл. По таблице интегралов находим, что 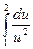 =
=  . Воспользуемся свойством 3 определенного интеграла, позволяющим менять границы интегрирования, при этом избавляясь от знака "минус" перед определенным интегралом (
. Воспользуемся свойством 3 определенного интеграла, позволяющим менять границы интегрирования, при этом избавляясь от знака "минус" перед определенным интегралом (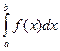 =-
=- 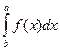 ). Тогда
). Тогда  =
=  =
= 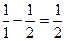 . Еще раз отметим, что к переменной х после смены границ интегрирования возвращаться не нужно!
. Еще раз отметим, что к переменной х после смены границ интегрирования возвращаться не нужно!
Ответ:  =
= 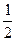 .
.
Пример 22.3. Вычислите  .
.
Решение. 1. Выполним подстановку u=lnx с целью прийти к интегралу от функции f(u) = и2.
2. Найдем du по формуле du=и'dx: du=(lnx)'dx = 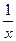 dx.
dx.
3. Выразим dx из выражения пункта 2 (du= 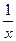 dx):
dx): 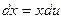 .
.
4. Подставим и и dx в исходный интеграл (пока неопределенный):  =
=  . Видим, что х можно сократить и прийти к интегралу относительно переменной и:
. Видим, что х можно сократить и прийти к интегралу относительно переменной и:  .
.
5. Вычислим новые границы интегрирования для переменной и. Для этого подставим существующие границы (1, e) в выражение u= lnx.
Тогда нижняя граница u1 = ln1= 0; верхняя граница u2 = lne= 1.
В результате всех преобразований первоначальный интеграл примет вид:  .
.
6. Вычислим полученный интеграл:  =
= 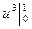 ==13-0=1.
==13-0=1.
Ответ:  =1.
=1.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 773; Нарушение авторских прав?; Мы поможем в написании вашей работы!