В геометрии

План:

1. Геометрический смысл определенного интеграла
2. Приложение определенного интеграла к вычислению площадей плоских фигур.
3. Вычисление длины дуги плоской кривой и объема тел вращения.

1. Геометрический смысл определенного интеграла.

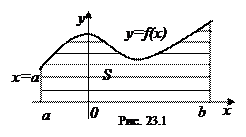Геометрический смысл определенного интеграла связан с понятием криволинейной трапеции.

х=b

Рассмотрим функцию y=f(x), непрерывную на отрезке [ a;b ] и принимающую на нем неотрицательные значения (f(x) ≥0). Фигуру, ограниченную сверху графиком функции y=f(x), сбоку – прямыми х=а и х = b, снизу – отрезком [ a;b ] оси Ох, называют криволинейной трапецией (рис. 23.1).

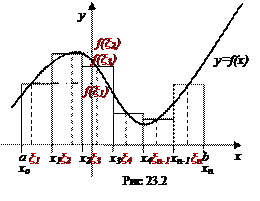Вспомним принцип введения определенного интеграла. Мы составляли интегральные суммы Sn, задающиеся формулой: Sn= .

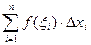Поскольку на отрезке [ a;b ] функция y=f(x) принимает неотрицательные значения, то каждое слагаемое интегральной суммы равно площади прямоугольника с основанием Δ х_i и высотой f (ξ _i) (i =1,2,…, п). А вся сумма Sn равна площади "ступенчатой фигуры", получающейся объединением рассматриваемых прямоугольников (рис. 23.2).

Обозначим площадь искомой криволинейной трапеции S. Она приближенно будет равна площади ступенчатой фигуры Sn: S ≈ Sn = 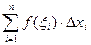. Чем меньше будет длина каждого отрезка Δ х_i, тем точнее приближение. Поэтому за точное значение площади S криволинейной трапеции принимается предел, к которому стремится площадь ступенчатой фигуры Sn, когда п неограниченно возрастает так, что λ=maxΔ х_i →0.

Итак, S= 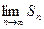= 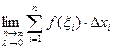, а это есть ни что иное, как определенный интеграл 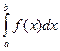. Получили, что S= 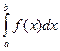. Следовательно, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми х=а и х = b, отрезком [ a;b ] оси Ох. В этом и заключается геометрический смысл определенного интеграла.

1. Приложение определенного интеграла к вычислению площадей плоских фигур.

При нахождении площадей плоских фигур, ограниченных некоторыми линиями, удобно использовать следующий алгоритм:

1. Построить фигуру, площадь которой требуется найти.
2. В соответствии с таблицей 23.1. определить вид фигуры и составить формулу для вычисления площади фигуры. Следует обратить внимание на границы интегрирования. Если они не следуют непосредственно из условия задачи, а определяются пересечением графиков каких-либо функций, то границы интегрирования следует находить аналитически, приравнивая соответствующие функции.
3. Вычислить площадь фигуры. Следует помнить, что площадь есть число положительное.

При составлении таблицы 23.1. учитывалось свойство аддитивности площади: если фигура состоит из двух и более частей, то для нахождения площади фигуры нужно сложить площади ее частей (рис. 23.3).

Таблица 23.1

Дата добавления: 2014-12-27