Несобственные интегралы I рода

Лекция 24. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

План:

1. Понятие несобственного интеграла
2. Несобственные интегралы I рода.
3. Несобственные интегралы II рода.

1. Понятие несобственного интеграла

Несобственными будем считать интегралы двух видов:

1. Определённые интегралы от непрерывной функции, у которых один или оба пределы интегрирования равны бесконечности: 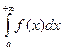, , 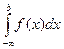. Их называют несобственными интегралами I рода.
2. Определённые интегралы от разрывной функции с конечными пределами интегрирования. Их называют несобственными интегралами II рода.

Рассмотрим нахождение обоих видов несобственных интегралов.

Пусть задана функция y=f(x), непрерывная на промежутке [ a;+∞). Если существует конечный предел 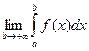, то его называют несобственным интегралом первого рода и обозначают .

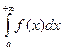Таким образом, по определению = .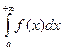

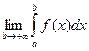Если найденный предел равен конечному числу, то говорят, что несобственный интеграл 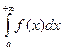сходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл 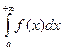расходится.

Геометрический смысл несобственного интеграла I рода заключается в следующем: если 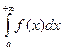сходится (при условии, что f(x) ≥0), то он представляет собой площадь "бесконечно длинной" криволинейной трапеции (рис. 24.1).

Аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом интегрирования для непрерывной на промежутке (-∞; b ] функции: = .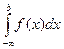

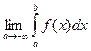Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой: = + , где с – произвольное число.

Рассмотрим примеры нахождения несобственных интегралов I рода.

Пример 24.1. Вычислите несобственный интеграл или установите его расходимость: .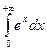

Решение. Для нахождения несобственного интеграла с бесконечной верхней границей от непрерывной функции воспользуемся формулой: 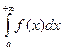= 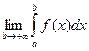. Тогда 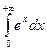= . Сначала вычислим интеграл от е^х:

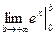= = = =∞. Получили, что несобственный интеграл расходится.

Ответ: 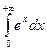расходится.

Пример 24.2. Вычислите несобственный интеграл или установите его расходимость: .

Решение. Подынтегральная функция 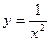непрерывна на промежутке (-∞; - 1]. Для нахождения несобственного интеграла I рода с бесконечной нижней границей воспользуемся формулой: 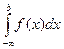= 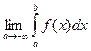. Тогда = . Вычислим интеграл, содержащийся под знаком предела: = 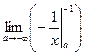. Избавимся от знака "минус", поменяв границы интегрирования местами:

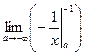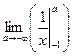= = = =1. Получили, что рассматриваемый несобственный интеграл сходится.

Ответ: =1.

1. Несобственные интегралы II рода.

Пусть задана функция y=f(x), непрерывная на промежутке [ a;b). Пусть b – точка разрыва второго рода. Если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают .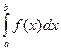

Таким образом, по определению = .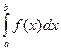

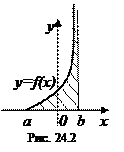Если найденный предел равен конечному числу, то говорят, что несобственный интеграл сходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл расходится.

Геометрический смысл несобственного интегралаII рода 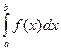, где b – точка разрыва второго рода, f(x) ≥0, заключается в следующем: если 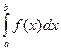сходится, то он представляет собой площадь "бесконечно высокой" криволинейной трапеции (рис. 24.2).

Аналогично вводится понятие несобственного интеграла II рода для непрерывной на промежутке (a;b ]функции при условии, что а – точка разрыва второго рода: = .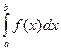

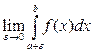Пример 24.3. Вычислите несобственный интеграл II рода: .

Решение. Подынтегральная функция 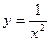непрерывна на промежутке (0;1], причем х= 0 - точка разрыва второго рода (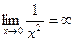). Для вычисления несобственного интеграла воспользуемся формулой: 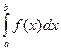= 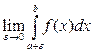. Получим, что

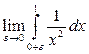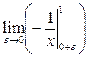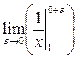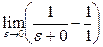= = = = = = ∞. Видим, что несобственный интеграл II рода расходится.

Ответ: расходится.

Контрольные вопросы:

1. Что называют несобственным интегралом?
2. Какие интегралы называются несобственными интегралами первого рода?
3. В чем заключается геометрический смысл несобственного интеграла первого рода?
4. Какие несобственные интегралы называют сходящимися, а какие расходящимися?
5. Какие интегралы называются несобственными интегралами второго рода?
6. В чем заключается геометрический смысл несобственного интеграла второго рода?

СПИСОК ЛИТЕРАТУРЫ:

1. Абдрахманова И.В. Элементы высшей математики: учеб. пособие – М.: Центр интенсивных технологий образования, 2003. – 186 с.

2. Алгебра и начала анализа (Ч.1, Ч.2): Учебник для ССУЗов / под ред. Г.Н.Яковлева. – М.: Наука, 1981.

3. Александрова Н.В. Математические термины. Справочник.- М.: Высш. школа, 1978. - 190 с.

4. Валуце И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб. пособие. – М.: Наука, 1989. – 576 с.

5. Григорьев В.П., Дубинский Ю.А. Элементы высшей математики: Учеб. для студ. учреждений СПО. - М.: Издательский центр "Академия", 2004. – 320с.

6. Лисичкин В.Т., Соловейчик И.Л. Математика: учеб. пособие для техникумов. – М.: Высш. школа, 1991. – 480 с.

7. Луканкин Г.Л., Мартынов Н.Н., Шадрин Г.А., Яковлев Г.Н. Высшая математика: учеб. пособие для студентов пед. институтов. – М.: Просвещение, 1988. – 431 с.

8. Письменный Д.Т. Конспект лекций по высшей математике: Ч.1. – М.:Айрис-пресс, 2006.- 288 с.

9. Филимонова Е.В. Математика: учеб. пособие для ссузов. – Ростов н/Д: Феникс, 2003. – 384 с.

10. Шипачев В.С. Высшая математика: учебник для вузов. – М.: Высшая школа, 2003. – 479 с.

11. Шипачев В.С. Курс высшей математики: высшее образование. – М.: ПРОЮЛ М.А.Захаров, 2002. – 600 с.

12. Энциклопедия для детей. Т.11. Математика / Глав. ред. М.В.Аксенова. - М.: Аванта+, 2000.- 688 с.

Дата добавления: 2014-12-27