
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия. 1. Понятие дифференциального уравнения
|
|
|
|
План:
1. Понятие дифференциального уравнения.
2. Простейшие дифференциальные уравнения первого порядка.
3. Дифференциальные уравнения с разделенными и разделяющимися переменными.
4. Приложение дифференциальных уравнений.
- Понятие дифференциального уравнения
При решении различных задач математики, физики, химии и других наук часто используют математические модели в виде уравнений, связывающих основные параметры изучаемого процесса. И поскольку скорость изменения величин можно рассматривать как производную некоторой функции, то ряд уравнений содержат и искомую функцию, и производную этой функции.
Так, зависимость массы m вещества, вступившего в химическую реакцию, от времени t описывается уравнением: 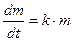 или
или 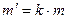 , где k – коэффициент пропорциональности. "Закон размножения бактерий" (зависимость массы бактерий m от времени t) также описывается уравнением:
, где k – коэффициент пропорциональности. "Закон размножения бактерий" (зависимость массы бактерий m от времени t) также описывается уравнением: 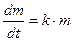 или
или 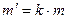 , где k> 0.
, где k> 0.
Закон радиоактивного распада вещества (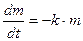 ), закон изменения температуры тела в зависимости от времени (
), закон изменения температуры тела в зависимости от времени (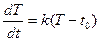 ), закон изменения давления воздуха в зависимости от высоты над уровнем моря (
), закон изменения давления воздуха в зависимости от высоты над уровнем моря (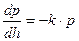 ) – все это примеры использования подобных уравнений в практике. Уже приведенные примеры указывают на их исключительную роль при решении разнообразных задач.
) – все это примеры использования подобных уравнений в практике. Уже приведенные примеры указывают на их исключительную роль при решении разнообразных задач.
Особенностью рассмотренных выше уравнений является то, что неизвестной оказывается не одно число или пара чисел, а функция. Причем неизвестная функция находится под знаком производной. Уравнения, содержащие производные или дифференциал искомой функции называют дифференциальными уравнениями.
Например, уравнения  ,
, 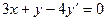 ,
, 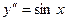 ,
, 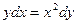 являются дифференциальными уравнениями.
являются дифференциальными уравнениями.
Наивысший порядок производной неизвестной функции, входящей в уравнение, называют порядком дифференциального уравнения.
Так, 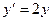 ,
, 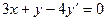 ,
, 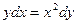 - дифференциальные уравнения первого порядка,
- дифференциальные уравнения первого порядка, 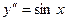 - дифференциальное уравнение второго порядка.
- дифференциальное уравнение второго порядка.
Решением дифференциального уравнения называется функция, подстановка которой в уравнение обращает его в тождество.
Пример 38.1. Докажите, что функция 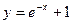 является решением дифференциального уравнения
является решением дифференциального уравнения 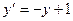 .
.
Решение. Найдем производную функции 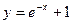 :
: 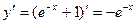 . Подставим известное у и найденное
. Подставим известное у и найденное 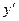 в дифференциальное уравнение
в дифференциальное уравнение 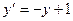 :
:
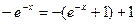

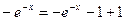 .
.
Получили, что 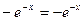 - верное равенство, следовательно, функция
- верное равенство, следовательно, функция 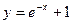 является решением дифференциального уравнения
является решением дифференциального уравнения 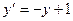 .
.
Любое дифференциальное уравнение имеет не одно, а множество решений, отличающихся друг от друга на константу С. Такое множество решений получило название общего решения дифференциального уравнения. Геометрически его можно изобразить в виде семейства интегральных кривых.
При решении задач часто необходимо из всей совокупности решений дифференциального уравнения выделить одно, отвечающее конкретным требованиям. Для этого задают начальные условия: 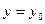 при
при 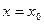 . Геометрически это означает, что нужно выделить отдельную интегральную кривую, проходящую через точку
. Геометрически это означает, что нужно выделить отдельную интегральную кривую, проходящую через точку 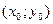 .
.
Задача нахождения решения дифференциального уравнения, удовлетворяющего условию 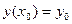 , называется задачей Коши, а полученное решение называется частным решением дифференциального уравнения.
, называется задачей Коши, а полученное решение называется частным решением дифференциального уравнения.
- Простейшие дифференциальные уравнения первого порядка
Рассмотрим дифференциальные уравнения первого порядка.
Уравнения вида 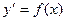 назовём простейшими диф. уравнениями первого порядка.
назовём простейшими диф. уравнениями первого порядка.
Например, уравнения 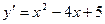 ,
,  - простейшие дифференциальные уравнения первого порядка. Обращаем внимание, что в левой части уравнения находится только
- простейшие дифференциальные уравнения первого порядка. Обращаем внимание, что в левой части уравнения находится только 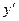 , а в правой – выражение, содержащее только переменную х.
, а в правой – выражение, содержащее только переменную х.
Для решения простейших дифференциальных уравнений первого порядка достаточно взять интеграл от правой и левой части по переменной х: 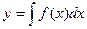 .
.
Пример 38.2. Найдите решение дифференциального уравнения 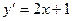 .
.
Решение. Поскольку перед нами простейшее дифференциальное уравнение первого порядка, найдем его решение по формуле 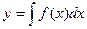 :
:
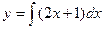 ;
;
у = 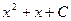 - общее решение дифференциального уравнения
- общее решение дифференциального уравнения 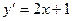 .
.
Ответ: у = 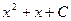 .
.
Пример 38.3. Найдите решение задачи Коши: 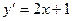 , если
, если  .
.
Решение. Общее решение заданного дифференциального уравнения имеет вид: у= = 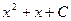 (см. пример 38.2). Воспользуемся начальными условиями:
(см. пример 38.2). Воспользуемся начальными условиями:  , следовательно, при
, следовательно, при 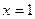
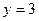 . Подставим эти числа в общее решение:
. Подставим эти числа в общее решение:
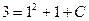 . Выразим из данного уравнения С:
. Выразим из данного уравнения С: 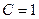 .
.
Подставив найденное значение С в общее решение у = 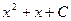 , получим следующее частное решение дифференциального уравнения: у =
, получим следующее частное решение дифференциального уравнения: у = 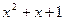 .
.
Ответ: у = 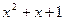 .
.
- Дифференциальные уравнения с разделенными и разделяющимися переменными.
Наиболее простым дифференциальным уравнением первого порядка является уравнение вида: 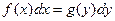 . В нем в левой части стоит функция f (x), зависящая только от переменной х, а в правой – функция g (y), зависящая только от переменной у. Такое дифференциальное уравнение называют уравнением с разделенными переменными.
. В нем в левой части стоит функция f (x), зависящая только от переменной х, а в правой – функция g (y), зависящая только от переменной у. Такое дифференциальное уравнение называют уравнением с разделенными переменными.
Для нахождения решения такого уравнения достаточно взять интеграл от обеих частей: 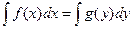 .
.
Пример 38.4. Найдите решение дифференциального уравнения: 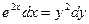 .
.
Решение. Данное дифференциальное уравнение представляет собой уравнение с разделенными переменными. Проинтегрируем обе части уравнения:
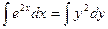 . Тогда
. Тогда
 - общее решение дифференциального уравнения
- общее решение дифференциального уравнения 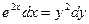 .
.
Ответ:  .
.
Если дифференциальное уравнение путем преобразований можно привести к виду 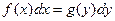 , то оно называется дифференциальным уравнением с разделяющимися переменными.
, то оно называется дифференциальным уравнением с разделяющимися переменными.
Для решения такого уравнения необходимо:
1. Если в уравнении встречается 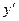 , то представить его как
, то представить его как 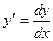 .
.
2. Произвести разделение переменных (в одной части при dx собрать выражения, содержащие только переменную х; в другой части при dу собрать выражения, содержащие только переменную у).
3. Почленно проинтегрировать уравнение с разделенными переменными.
Пример 38.5. Найдите решение дифференциального уравнения: 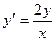 .
.
Решение. Данное уравнение – дифференциальное уравнение с разделяющимися переменными. Представим 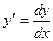 , тогда
, тогда 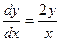 или
или 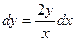 .
.
Будем собирать множители с у в левой части, с х – в правой: 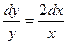 .
.
Интегрируя обе части, получим: 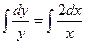 или
или 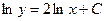 - общее решение.
- общее решение.
Ответ: 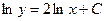 .
.
Замечание. Иногда при нахождении решения дифференциального уравнения, каждое слагаемое которого представляет собой натуральный логарифм, в качестве константы можно выбирать 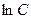 . Такую операцию можно было бы произвести в примере 38.5. Тогда общее решение дифференциального уравнения имело бы вид:
. Такую операцию можно было бы произвести в примере 38.5. Тогда общее решение дифференциального уравнения имело бы вид: 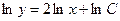 . Применим свойства логарифма:
. Применим свойства логарифма: 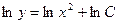 или
или 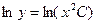 . Откуда можно заключить, что
. Откуда можно заключить, что 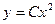 . Этот прием особенно эффективен при решении задачи Коши.
. Этот прием особенно эффективен при решении задачи Коши.
- Приложение дифференциальных уравнений.
Как уже отмечалось, дифференциальные уравнения находят широкое применение в практической деятельности человека. Рассмотрим некоторые задачи, сводящиеся к решению дифференциальных уравнений.
Пример 38.6. Составить уравнение линии, проходящей через точку М (2;-3) и имеющей в каждой точке угловой коэффициент касательной 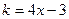 .
.
Решение. Обратимся к геометрическому смыслу производной: k = 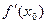 или
или 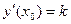 . Поскольку
. Поскольку 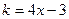 задано в условии задачи, то можно составить уравнение:
задано в условии задачи, то можно составить уравнение:
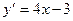 - простейшее дифференциальное уравнение первого порядка.
- простейшее дифференциальное уравнение первого порядка.
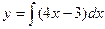

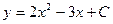 - семейство линий, имеющих в каждой точке угловой коэффициент касательной
- семейство линий, имеющих в каждой точке угловой коэффициент касательной 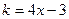 .
.
Выделим уравнение одной линии, проходящей через точку М (2;-3). Подставим в уравнение 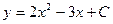 значения
значения 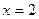 и
и 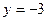 :
:
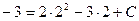

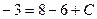

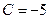 .
.
Получили, что 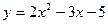 - уравнение линии, проходящей через точку М (2;-3) и имеющей в каждой точке угловой коэффициент касательной
- уравнение линии, проходящей через точку М (2;-3) и имеющей в каждой точке угловой коэффициент касательной 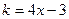 .
.
Ответ: 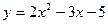 .
.
Пример 38.7. Тело движется прямолинейно со скоростью 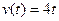 . Найдите закон движения тела, если при
. Найдите закон движения тела, если при 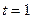 тело находилось в начале координат.
тело находилось в начале координат.
Решение. Воспользуемся физическим смыслом производной: 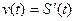 . Поскольку
. Поскольку 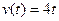 задано в условии задачи, то можно составить уравнение:
задано в условии задачи, то можно составить уравнение:
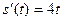 - простейшее дифференциальное уравнение первого порядка.
- простейшее дифференциальное уравнение первого порядка.
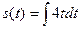

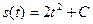 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Найдем частное решение этого уравнения. Поскольку по условию при 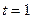 тело находилось в начале координат, подставим в уравнение
тело находилось в начале координат, подставим в уравнение 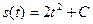 значения
значения 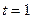 и
и 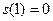 :
: 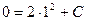

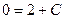

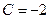 .
.
Подставляя С в общее решение, получим, что 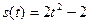 - искомый закон движения тела.
- искомый закон движения тела.
Ответ: 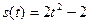 .
.
Контрольные вопросы:
- Что называют дифференциальным уравнением?
- Что такое порядок дифференциального уравнения?
- Что называют решением дифференциального уравнения? Какова геометрическая интерпретация множества решений дифференциального уравнения?
- Какая задача получила название задачи Коши?
- Какие процессы в окружающем мире описываются с помощью дифференциальных уравнений?
- Какое уравнение называют простейшим дифференциальным уравнением первого порядка? Каков принцип его решения?
- Какие дифференциальные уравнения называют уравнениями с разделенными и разделяющимися переменными? Каков метод их решения?
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 715; Нарушение авторских прав?; Мы поможем в написании вашей работы!