Лекция 41. Дифференциальные уравнения второго порядка

План:

1. Простейшие дифференциального уравнения второго порядка.

2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

1. Простейшие дифференциального уравнения второго порядка

Напомним, что дифференциальным уравнением второго порядка называется уравнение, наивысший порядок производной или дифференциалов в котором равен двум.

Простейшим дифференциальным уравнением второго порядка назовем уравнение вида: .

Например, уравнения , 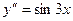- простейшие дифференциальные уравнения второго порядка. Подчеркнем, что в левой части простейшего дифференциального уравнения находится только , а в правой – выражение, содержащее только переменную х.

Для решения простейших дифференциальных уравнений второго порядка необходимо двукратное интегрирование по переменной х.

Рассмотрим принцип решения простейших дифференциальных уравнений второго порядка на следующем примере:

Пример 41.1. Найдите решение дифференциального уравнения .

Решение. Поскольку перед нами простейшее дифференциальное уравнение второго порядка, найдем сначала 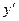по формуле: .

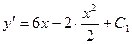или , где С ₁ – константа.

Для нахождения искомой функции у найдем интеграл от 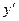по переменной х:

или 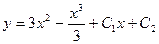, где С ₁ и С ₂ – константы.

Полученная функция является общим решением дифференциального уравнения . Ответ: .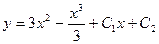

Отметим, что общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные С ₁ и С ₂.

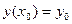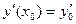Для простейшего дифференциального уравнения второго порядка можно рассмотреть задачу Коши (см. лекцию 38). Только в отличие от дифференциальных уравнений первого порядка, необходимо иметь два начальных условия: и . Для нахождения частного решения задачи Коши можно использовать следующий алгоритм:

1. Найти 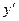по формуле: .
2. Воспользовавшись первым начальным условием (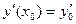), найти значение константы С ₁ и подставить его в функцию .
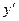3. Найти функцию у как интеграл от 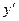по переменной х.
4. Воспользовавшись вторым начальным условием (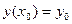), найти значение константы С ₂ и подставить его в функцию 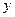. Полученная функция 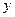и будет являться частным решением исходного дифференциального уравнения.

Пример 41.2. Найдите решение задачи Коши: 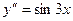, если при и .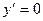

Решение. 1. Найдем .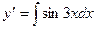

2. Воспользуемся первым начальным условием: 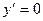при . Подставим эти числа в функцию 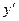: 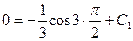. Поскольку 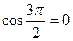, получим, что .

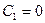Подставим найденное значение С ₁ в функцию 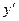: или .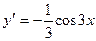

3. Найдем функцию у: или .

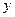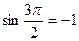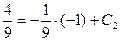
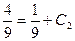
4. Воспользуемся вторым начальным условием: при . Подставим эти числа в функцию : . Поскольку , получим: или .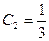

Найденное значение константы С ₂ подставим в функцию 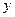: 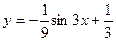. Полученная функция является частным решением исходного дифференциального уравнения 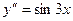при заданных начальных условиях.

Ответ: .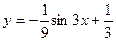

1. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида , где p и q – постоянные величины.

Например, уравнения 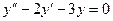, , 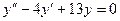являются линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами

Для нахождения решения дифференциальных уравнений такого вида будем составлять характеристическое уравнение: 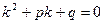, где k – некоторая новая переменная. Характеристическое уравнение является квадратным относительно k.

В зависимости от числа и вида корней данного характеристического уравнения, решение исходного дифференциального уравнения можно представить в виде таблицы 4.1:

Таблица 41.1

Дата добавления: 2014-12-27