
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Первого порядка
Лекция 39. ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
План:
1. Понятие однородного дифференциального уравнения первого порядка.
2. Методика решения однородных дифференциальных уравнений первого порядка.
- Понятие однородного дифференциального уравнения первого порядка
Введем сперва понятие однородной функции: функция 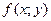 называется однородной функцией п-го порядка, если при умножении каждого ее аргумента на произвольный множитель вся функция умножится на λп, т.е.
называется однородной функцией п-го порядка, если при умножении каждого ее аргумента на произвольный множитель вся функция умножится на λп, т.е. 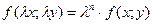 .
.
Пример 39.1. Доказать, что функции  и
и  - однородные функции второго порядка.
- однородные функции второго порядка.
Решение. Рассмотрим функцию  . Подставим в нее вместо х → λх, а вместо у → λу:
. Подставим в нее вместо х → λх, а вместо у → λу:
 =
= 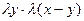 =
=  . Получили, что
. Получили, что  , следовательно, по определению
, следовательно, по определению  - однородная функция второго порядка.
- однородная функция второго порядка.
Рассмотрим функцию  . Аналогично подставив в нее вместо х → λх, а вместо у → λу, получим:
. Аналогично подставив в нее вместо х → λх, а вместо у → λу, получим:  . То есть
. То есть 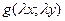 =
= 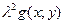 , откуда по определению
, откуда по определению  - однородная функция второго порядка.
- однородная функция второго порядка.
Дифференциальное уравнение вида  , где
, где 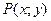 и
и  - однородные функции одинакового порядка, будем называть однородным.
- однородные функции одинакового порядка, будем называть однородным.
Так, дифференциальное уравнение  будет являться однородным в силу того, что обе функции при dx и dy – однородные второго порядка (см. пример 39.1).
будет являться однородным в силу того, что обе функции при dx и dy – однородные второго порядка (см. пример 39.1).
- Методика решения однородных дифференциальных уравнений первого порядка
Однородное уравнение можно преобразовать к уравнению с разделяющимися переменными при помощи подстановки 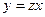 , где
, где  - новая неизвестная функция.
- новая неизвестная функция.
Найдем dy по правилу нахождения производной произведения:  или
или 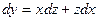 .
.
Сформулируем алгоритм решения однородных дифференциальных уравнений:
- Выполнить подстановки:
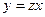 и
и 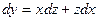 . В получившемся дифференциальном уравнении раскрыть скобки и привести подобные слагаемые. Должно получиться уравнение с разделяющимися переменными.
. В получившемся дифференциальном уравнении раскрыть скобки и привести подобные слагаемые. Должно получиться уравнение с разделяющимися переменными. - Проинтегрировать обе части уравнения с разделяющимися переменными относительно переменных x и z. Найти общее решение дифференциального уравнения.
- В общем решении вернуться к переменным x и у, подставив вместо z выражение:
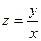 .
. - Выписать в ответе получившееся общее решение дифференциального уравнения.
Пример 39.2. Найдите решение дифференциального уравнения:  .
.
Решение. Данное уравнение – однородное дифференциальное уравнение первого порядка.
1. Выполним подстановки: 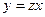 и
и 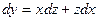 :
:
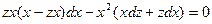 .
.
Раскроем скобки:
 .
.
Приведем подобные слагаемые: первое и последнее взаимно уничтожаются. Получим:
 .
.
Перед нами уравнение с разделяющимися переменными. Соберем в левой части выражения, содержащие dx, в правой – выражения, содержащие dу.
 .
.
Тогда 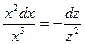 или
или  - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.
2. Интегрируя обе части, получим: 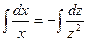 или
или  .
.
3. Подставим вместо z выражение: 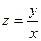 :
:  или
или  . Это и есть общее решение исходного однородного дифференциального уравнения.
. Это и есть общее решение исходного однородного дифференциального уравнения.
Ответ:  .
.
Контрольные вопросы:
- Какие функции называют однородными функциями п -го порядка?
- Каков общий вид однородного дифференциального уравнения первого порядка?
- Какие из приведенных ниже дифференциальных уравнений являются однородными: а)
 ; б)
; б) 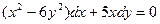 ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ?
? - Какова методика решения однородных дифференциальных уравнений первого порядка?
|
|
Дата добавления: 2014-12-27; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!