Лекция 14. Возрастание и убывание, экстремумы функций

План:

1. Признаки возрастания и убывания функции

2. Понятие точек экстремума и экстремумов функции

3. Необходимые условия существования экстремума

4. Достаточные условия существования экстремума

1. Признаки возрастания и убывания функции

Напомним определение возрастающей и убывающей функции на интервале .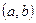

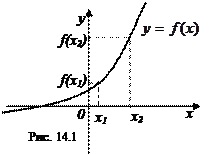Функция 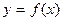называется возрастающей на интервале 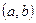, если большему значению аргумента соответствует большее значение функции, т.е. если 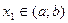, , 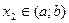, 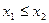то .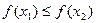

Пример возрастающей функции приведен на рис. 14.1.

Функция 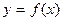называется убывающей на интервале 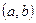, если большему значению аргумента соответствует большее значение функции, т.е. если 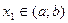, , 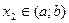, 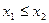то .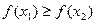

Пример убывающей функции приведен на рис. 14.2.

Интервалы, в которых функция либо только возрастает, либо только убывает, называются интервалами монотонности.

Сформулируем критерий возрастания и убывания функции:

Теорема. Пусть 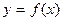- дифференцируемая на интервале 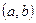функция. Функция 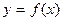возрастает на 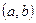тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка.

Функция 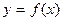убывает на 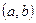тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.

Представим критерий возрастания и убывания функции в виде схемы:

f(x)ä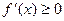
f(x) æ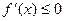

1. Понятие точек экстремума и экстремумов функции

Среди всех точек области определения функции наибольший интерес для нас будут представлять точки экстремума функции.

Введем понятие окрестности. Окрестностьюточки будем называть любой интервал 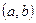, содержащий эту точку.

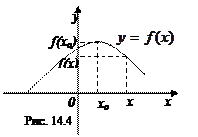Точка х_о из области определения функции 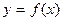называется точкой минимума функции, если для всех х из некоторой окрестности точки х_о выполнено неравенство: 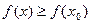(рис. 14.3).

Точка х_о из области определения функции 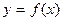называется точкой максимума функции, если для всех х из некоторой окрестности точки х_о выполнено неравенство: 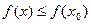(рис. 14.4).

Значения функции в точках минимума и максимума называются соответственно минимумом и максимумом функции.

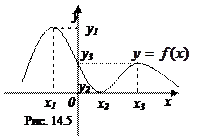Точки минимума и максимума называются точками экстремума функции, а максимум и минимум – экстремумами функции.

Функция может иметь несколько экстремумов.

Так, функция на рис. 14.5 имеет три точки экстремума (х₁, х₃ – точки максимума, х₂ – точка минимума) и, соответственно, три экстремума (у₁, у₃ – максимумы функции, у₂=0 – минимум).

1. Необходимые условия существования экстремума

Необходимое условие существования экстремума функции даёт теорема Ферма:

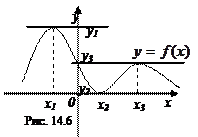Теорема Ферма. Если точка х_о – точка экстремума функции 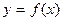и в ней существует производная f`(x_o), то эта производная равна нулю, т.е. f'(x_o) =0.

Эта теорема имеет простой геометрический смысл (рис. 14.6): касательные, проведенные к графику функции в точках экстремума (при условии существования в них производной, а, следовательно, единой касательной), параллельны оси ОХ. Угловой коэффициент α касательных, проведенных к графику функции в точках экстремума, равен 0, и в силу геометрического смысла производной (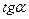 = 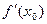), производная функции в этих точках обращается в ноль.

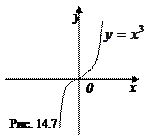Точки, в которых производная функции равна нулю или не существует, назовем критическими точками (первого рода). Только среди критических точек могут быть точки экстремума.

Но любая ли критическая точка является точкой экстремума? Рассмотрим всем хорошо известную функцию 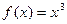. Найдем ее производную 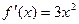и критические точки: 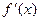=0 .

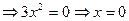Итак, 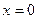является критической точкой функции 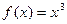, но она не является точкой экстремума. Таким образом, теорема Ферма дает только необходимые условия существования экстремума.

Чтобы выяснить, в каких критических точках функция имеет экстремум, рассмотрим достаточные условия существования экстремума.

1. Достаточные условия существования экстремума

Теорема. Пусть функция 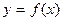непрерывна и дифференцируема в некоторой окрестности точки х_о. Тогда:

1. если производная 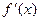при переходе через точку х_о меняет знак с плюса на минус, то точка х_о является точкой максимума;

2. если производная 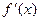при переходе через точку х_о меняет знак с минуса на плюс, то точка х_о является точкой минимума.

Представим критерий нахождения точек экстремума функции в виде схемы:

хо – критическая точка: f`(xо) =0 или f`(xо) не существует
хо – точка минимума	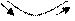хо	хо
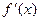
хо – точка максимума	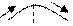хо	хо

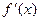
Для нахождения промежутков монотонности и экстремумов функции будем использовать следующий алгоритм:

1. Найти область определения функции.

2. Найти первую производную функции.

3. Определить критические точки первого рода (f'(x_o) =0 или f'(x_o) не существует).

4. На числовой оси отметить критические точки и определить знаки производной на каждом из получившихся интервалов.

5. Найти интервалы монотонности, выписать точки экстремума функции (если они есть), используя соответствующие критерии, вычислить значения функции в точках экстремума.

Пример 14.1. Найдите промежутки монотонности и экстремумы функции .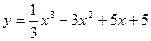

Решение. 1. Данная функция определена на множестве R.

2. Найдем первую производную функции: = .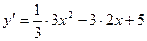

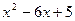3. Определим критические точки первого рода (у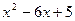' =0): =0;

х ₁=1 или х ₂=5.

4. На числовой оси отметим критические точки х ₁=1 и х ₂=5. Эти точки разбивают область определения функции на три интервала (-∞;1), (1;5); (5;+∞). Расставим знаки производной функции у' = 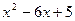на каждом из полученных интервалов:

при х =0 (-∞;1) у' (0)=5>0;

при х =2 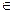(1;5) у' (2)= 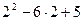=-3<0;

при х =6 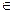(5;+∞) у' (6)= 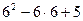=5>0.

т.min

т.max

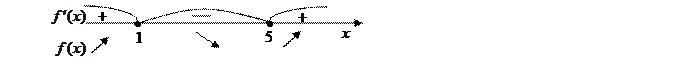
5. Согласно критерию возрастания и убывания функция 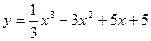возрастает при х (-∞;1] [5;+∞), убывает при х 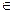[1;5].

Согласно критерию нахождения точек экстремума х =1 – точка максимума, х =5 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках: 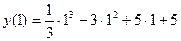= = 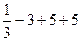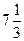- максимум функции;

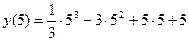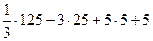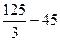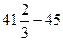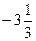= = = = - минимум функции.

Ответ: 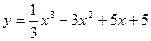возрастает при х (-∞;1] [5;+∞), убывает при х 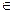[1;5];

х =1 – точка максимума; 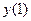= 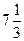- максимум функции;

х =5 – точка минимума; = 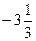- минимум функции.

Пример 14.2. Найдите промежутки монотонности и экстремумы функции .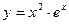

Решение. 1. Данная функция определена на множестве R.

2. Найдем первую производную функции по правилу производной произведения:

= =

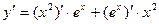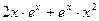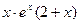
3. Определим критические точки первого рода (у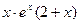' =0): =0;

х ₁=0 или 2+ х =0 (е^х ≠0 для всех х из множества R).

4. На числовой оси отметим критические точки х =-2 и х =0. Эти точки разбивают область определения функции на три интервала (-∞;-2), (-2;0); (0;+∞). Расставим знаки производной функции у'= 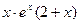на каждом из полученных интервалов:

т.min

т.max

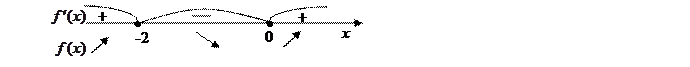
5. Согласно критерию возрастания и убывания функция 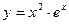возрастает при

х 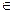(-∞;-2] 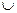[0;+∞), убывает при х 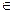[-2;0].

Согласно критерию нахождения точек экстремума х =-2 – точка максимума, х =0 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках: 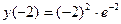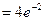= 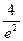- максимум функции;

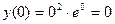- минимум функции.

Ответ: 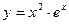возрастает при х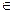 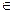(-∞;-2] 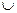[0;+∞), убывает при х 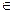[-2;0];

х =-2 – точка максимума; 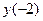= 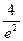- максимум функции;

х =5 – точка минимума; 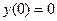- минимум функции.

Контрольные вопросы:

1. Какая функция называется возрастающей на интервале 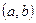? Какая функция называется убывающей на интервале ?
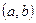2. В чем заключается критерий возрастания и убывания функции?
3. Что называют точками максимума и минимума функции? Каково их обобщающее название?
4. В чем отличие экстремумов от точек экстремума?
5. Какие точки функции называются критическими точками первого рода?
6. Всякая ли критическая точка является точкой экстремума?
7. В чем заключается критерий нахождения точек экстремума функции?

Дата добавления: 2014-12-27