Лекция 16. Асимптоты графика функции

План:

1. Понятие асимптот
2. Алгоритм поиска асимптот

1. Понятие асимптот

Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций 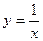, y=tgx, y=сtgx. Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.

Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.

Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:

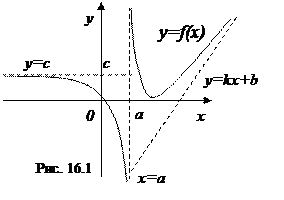
х=а – вертикальная асимптота  

у=c – горизонтальная асимптота  

у=kx+b – наклонная асимптота

Дадим определение каждому виду асимптот:

1. Прямая х=а называется вертикальной асимптотой функции 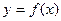, если .

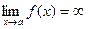2. Прямая у=с называется горизонтальной асимптотой функции 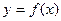, если .

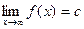3. Прямая у=kx+b называется наклонной асимптотой функции 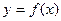, если .

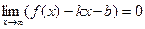Геометрически определение наклонной асимптоты означает, что при 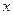→∞ график функции 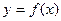сколь угодно близко подходит к прямой у=kx+b, т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.

Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии 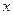→∞. Иногда их различают на горизонтальные и наклонные асимптоты при 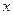→+∞ и →-∞.

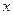1. Алгоритм поиска асимптот

Для поиска асимптот можно использовать следующий алгоритм:

1. Для поиска вертикальных асимптот находим точки, не принадлежащие области определения (х=а) и проверяем следующее условие: если 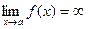, то х=а – вертикальная асимптота.

Вертикальных асимптот может быть одна, несколько или не быть совсем.

1. Для поиска горизонтальных асимптот находим .

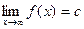• Если с – число, то у=с – горизонтальная асимптота;
• Если с – бесконечность, то горизонтальных асимптот нет.

1. Для поиска наклонных асимптот находим .

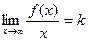• Если k – число, отличное от 0, то находим 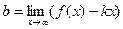. Тогда у=kx+b – наклонная асимптота;
• Если k – бесконечность, то наклонных асимптот нет.

Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.

Рассмотрим примеры нахождения асимптот функции:

Пример 16.1. Найдите асимптоты кривой .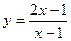

Решение. 1. Найдем область определения функции: х -1≠0; х ≠1.

Проверим, является ли прямая х= 1 вертикальной асимптотой. Для этого вычислим предел функции 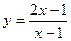в точке х= 1: .

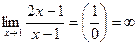Получили, что 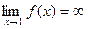, следовательно, х= 1 - вертикальная асимптота.

2. Для поиска горизонтальных асимптот находим 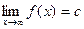: с = .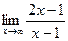

Поскольку в пределе фигурирует неопределенность 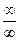, воспользуемся правилом Лопиталя: с = 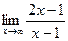= 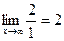. Т.к. с =2 (число), то у=2 – горизонтальная асимптота.

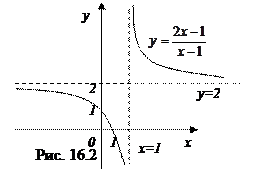Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.

Таким образом, данная функция имеет вертикальную асимптоту х= 1 и горизонтальную асимптоту у=2. Для наглядности график данной функции представлен на рис. 16.2.

Пример 16.2. Найдите асимптоты кривой .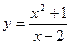

Решение. 1. Найдем область определения функции: х -2≠0; х ≠2.

Проверим, является ли прямая х= 2 вертикальной асимптотой. Для этого вычислим предел функции 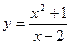в точке х= 2: .

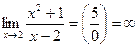Получили, что 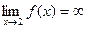, следовательно, х= 2 - вертикальная асимптота.

2. Для поиска горизонтальных асимптот находим 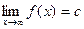: с = .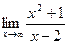

Поскольку в пределе фигурирует неопределенность 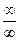, воспользуемся правилом Лопиталя: с = 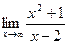= 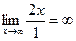. Т.к. с – бесконечность, то горизонтальных асимптот нет.

3. Для поиска наклонных асимптот находим :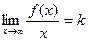

= = = .

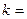
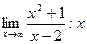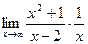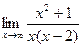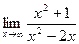Получили неопределенность вида 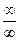, воспользуемся правилом Лопиталя: 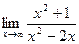= =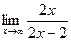1.Итак, 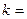1. Найдем b по формуле: .

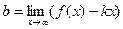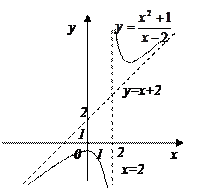b= = =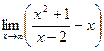

= = .

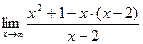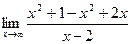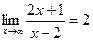Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.

Рис. 16.3

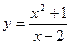Таким образом, данная функция имеет вертикальную асимптоту х= 2 и наклонную асимптоту у=x+2. Для наглядности график функции представлен на рис. 16.3.

Контрольные вопросы:

1. Что называют вертикальной, горизонтальной и наклонной асимптотой?
2. Сколько у функции может существовать вертикальных асимптот?
3. Может ли функция вообще не иметь асимптот?
4. Как обозначаются асимптоты на графике функции?
5. Какие из данных линий могут быть асимптотами: х= -4; у=-2x+6; у=x²+6; у=-3; х= 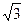; ; 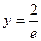х=0; у=- 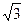x. Определите их вид.

Лекция 17. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА

В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути – уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.

С учетом всех вышеперечисленных аспектов приведем схему исследования функции и построения графика.

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность:

· если 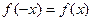, то функция четная (график четной функции симметричен относительно оси Оу);

· если 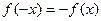, то функция нечетная (график нечетной функции симметричен относительно начала координат);

· в противном случае функция ни четная, ни нечетная.

3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).

4. Найти точки пересечения графика функции с осями координат:

· Ох: у =0 (решаем уравнение лишь в том случае, если можем использовать известные нам методы);

· Оу: х =0.

5. Найти первую производную функции и критические точки первого рода.

6. Найти интервалы монотонности и экстремумы функции.

7. Найти вторую производную функции и критические точки второго рода.

8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.

9. Найти асимптоты графика функции.

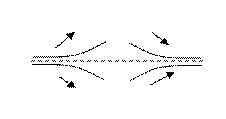
10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот:

вертикальной	горизонтальной	наклонной

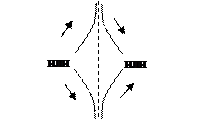
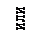
11. При необходимости выбрать контрольные точки для более точного построения.

Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:

Пример 17.1. Постройте график функции .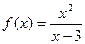

Решение. 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.

2. Для определения четности и нечетности функции найдем :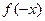

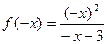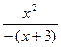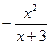= = . Видим, что 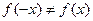и 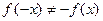, следовательно, функция 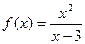ни четная, ни нечетная.

3. Функция непериодическая.

4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у =0. Получим уравнение: 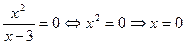. Итак, точка (0; 0) – точка пересечения с осями координат.

5. Найдем производную функции по правилу дифференцирования дроби: = = = = .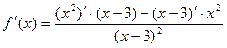

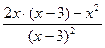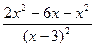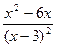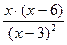Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.

, если 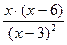=0, следовательно, 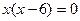. Произведение тогда равно 0, когда хотя бы один из множителей равен 0: 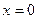или .

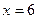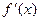не существует, если знаменатель (х -3)² равен 0, т.е. 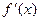не существует при х =3.

Итак, функция имеет три критические точки первого рода: ; ; .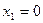

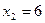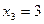6. На числовой оси отметим критические точки первого рода, причем точку 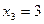отмечаем выколотой точкой, т.к. в ней функция не определена.

Расставляем знаки производной 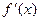= 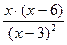на каждом промежутке:

т.min

т.max

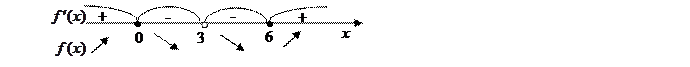
На промежутках, где 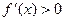, исходная функция возрастает (при 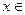(-∞;0] 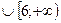), где 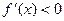- убывает (при 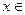[0;3) 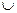(3;6]).

Точка х =0 является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: .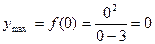

Точка х =6 является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: .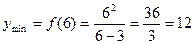

Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.

Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.

Последняя строка служит для обозначения максимума и минимума функции.

х	(-∞;0)		(0;3)		(3;6)		(6;+ ∞)
	+		-		-		+
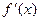
f(x)
Выводы		max				min

7. Найдем вторую производную функции как производную от первой производной: = =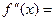

= .

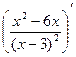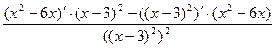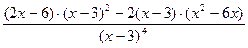Вынесем в числителе х -3 за скобки и выполним сокращение:

= .

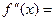
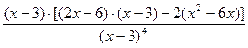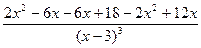Приведем в числителе подобные слагаемые: .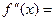

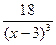Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.

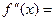0, если 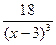=0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.

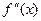не существует, если знаменатель (х -3)³ равен 0, т.е. 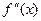не существует при х =3.

Итак, функция имеет одну критическую точку второго рода: .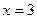

8. Найдем интервалы выпуклости и точки перегиба графика функции.

На числовой оси отметим критическую точку второго рода выколотой точкой, т.к. в ней функция не определена.

Расставляем знаки второй производной 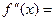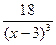на каждом промежутке:

На промежутках, где 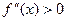, исходная функция вогнута (при 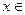(3;+∞)), где 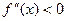- выпукла (при 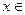(-∞;3)).

Точка х =3 не является точкой перегиба графика функции, т.к. в ней исходная функция не определена.

9. Найдем асимптоты графика функции.

9.1. Поскольку область определения функции – все действительные числа за исключением х =3, то проверим, является ли прямая х= 3 вертикальной асимптотой. Для этого вычислим предел функции 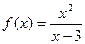в точке х= 3: .

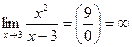Получили, что 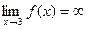, следовательно, х= 3 - вертикальная асимптота.

9.2. Для поиска горизонтальных асимптот находим 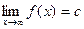: с = .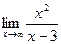

Поскольку в пределе фигурирует неопределенность 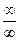, воспользуемся правилом Лопиталя: с = 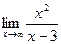= 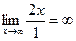. Т.к. с – бесконечность, то горизонтальных асимптот нет.

9.3. Для поиска наклонных асимптот находим :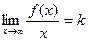

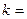
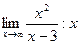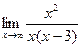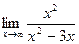= = =1.

Итак, 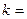1. Найдем b по формуле: .

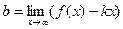b= = = = .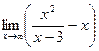

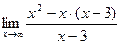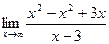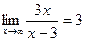Получили, что b= 3. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+3.

Таким образом, данная функция имеет вертикальную асимптоту х= 3 и наклонную асимптоту у=x+3.

10. По полученным ранее данным строим график функции (рис. 17.1). Поскольку к построению графика предъявляются высокие требования, система координат должна быть задана корректно: должно присутствовать обозначение осей Ох, Оу, начало отсчета, единицы измерения по каждой оси.

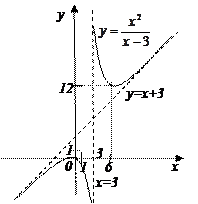Прежде чем строить график функции, нужно:

· провести асимптоты пунктирными линиями;

· отметить точки пересечения с осями координат;

·

Рис. 17.1

отметить максимум и минимум функции, причем рекомендуется прямо на чертеже обозначить максимум и минимум функции дугами: k или ;

· пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать.

· проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.

11. Для более точного построения можно выбрать несколько контрольных точек. Например, найдем значения функции в точках -2 и 7:

; .

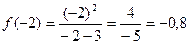Корректируем график с учетом контрольных точек.

Контрольные вопросы:

1. Каков алгоритм построения графика функции?
2. Может ли функция иметь экстремум в точках, не принадлежащих области определении?

ГЛАВА 3. 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

Дата добавления: 2014-12-27