Лекция 13. Производные и дифференциалы высших порядков. Правило Лопиталя

План:

1. Понятие производной высших порядков

2. Понятие дифференциала высших порядков

3. Правило Лопиталя

1. Понятие производной высших порядков

Пусть 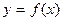- дифференцируемая на интервале 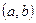функция. Тогда ее производная 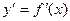- тоже функция, определенная на интервале 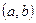. И у нее можно найти производную, называемую производной второго порядка или второй производной. Итак, производная от первой производной 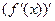называется второй производной функции и обозначается 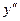или .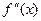

Пример 13.1. Найдите вторую производную функции .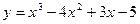

Решение. Найдем у': .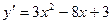

Найдем 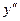как производную от у': = .

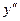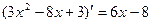Ответ: =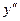

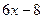
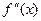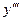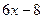Видим, что вторая производная – тоже функция, следовательно, существует производная второй производной () ', называемая третьей производной или . Так, в примере 13.1 =() ' =6.

Аналогично вводится определение четвертой производной ;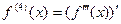

пятой производной ;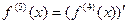

п -й производной .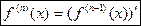

Таким образом, производной п-го порядка функции 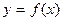называется производная от производной (п -1)-го порядка (если она существует).

Пример 13.2. Найдите четвертую производную функции .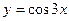

Решение. Найдем у' как производную сложной функции (и=3х):

.

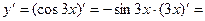
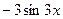Найдем 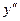как производную от у': =() ' = = .

=() ' = .

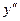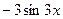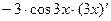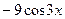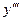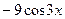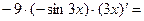
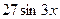у ⁽⁴⁾=() ' = = .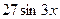

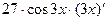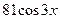Ответ: у ⁽⁴⁾= .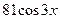

Пример 13.3. Найдите п -ю производную функции .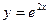

Решение. Найдем у ’ как производную сложной функции (и=2х):

= = .

=() ' = = .

=() ' = = .

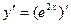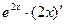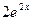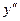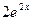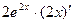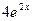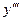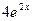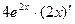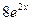Очевидно, что у ^(п)= .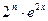

Ответ: у ^(п)= .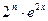

1. Понятие дифференциала высших порядков

С помощью производных высших порядков вводятся дифференциалы высших порядков. Как и производные, они определяются последовательно.

Так второй дифференциал d²y есть дифференциал от первого дифференциала, 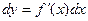при том же самом приращении Δ х.

Таким образом, d²y= d(dy) или .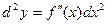

Аналогично ;

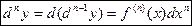
Итак, дифференциалом п-го порядка от функции 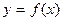называется дифференциал от дифференциала порядка п -1 при одном и том же приращении Δ х.

Рассмотрим пример нахождения дифференциала функции:

Пример 13.4. Найдите дифференциал четвертого порядка функции .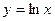

Решение. Найдем dy по формуле : = .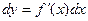

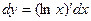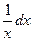Найдем 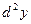по формуле 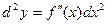: 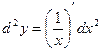= 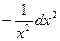. Для удобства нахождения последующих дифференциалов представим 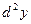как .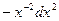

Тогда = .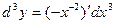

= .

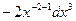
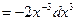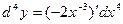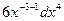
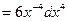
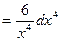Ответ: .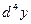

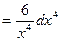1. Правило Лопиталя

В предыдущей главе мы учились находить пределы различных функций. Но всегда ли это возможно? Пусть нужно вычислить 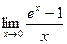. Любой предел мы начнем раскрывать с оценки: окажется, что перед нами неопределенность вида 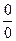. И никакой из ранее известных нам методов в данном случае неприменим.

Тогда на помощь придет правило Лопиталя. Под правилом Лопиталя понимают прием раскрытия неопределенностей вида 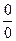или .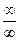

Теорема (правило Лопиталя). Для вычисления предела 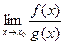, где 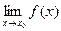= 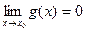, достаточно найти предел отношения производных данных функций (если он существует), т.е. = .

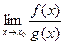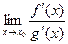Замечание. 1. Правило Лопиталя справедливо также для случаев

· неопределенности вида 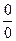при х →∞;

· неопределенности вида 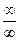при х → х_о и х →∞.

2. Правило Лопиталя может быть применено последовательно несколько раз для раскрытия неопределенностей вида 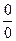или .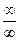

Рассмотрим примеры нахождения пределов функций с использованием правила Лопиталя.

Пример 13.5. Вычислите .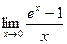

Решение. Поскольку в примере встречается неопределенность вида 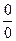, можно применить правило Лопиталя:

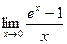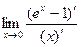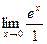= = = е⁰ =1.

Ответ: 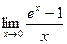=1.

Пример 13.6. Вычислите .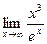

Решение. Поскольку в примере рассматривается неопределенность вида 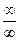, можно применить правило Лопиталя:

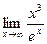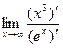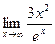= = . Снова получили неопределенность вида 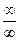, следовательно, можно применить правило Лопиталя еще раз:

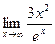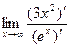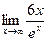= = . Повторно применяя правило Лопиталя, получим

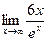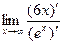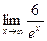= = =0, т.к. е^х →∞ при х →∞.

Ответ: 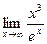=0.

Пример 13.7. Вычислите .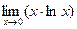

Решение. Поскольку при х →0 функция lnx →∞, то имеет место неопределенность вида 0∙∞ и правило Лопиталя применить нельзя. Попытаемся преобразовать выражение, стоящее под знаком предела: 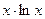= 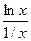. Тогда под знаком предела будет неопределенность вида 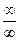, к которой правило Лопиталя применимо:

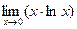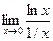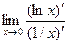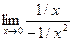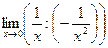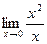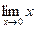= = = = =- =- =0.

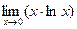Ответ: =0.

Контрольные вопросы.

1. Что называют второй производной функции ?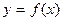

2. Что называют производной п -го порядка функции ?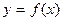

3. Что называют дифференциалом второго порядка функции ?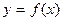

4. Что называют дифференциалом п -го порядка функции ?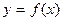

5. В каком случае для вычисления пределов применяется правило Лопиталя? Приведите формулировку правила Лопиталя.

6. Допустимо ли применять правило Лопиталя несколько раз подряд?

Дата добавления: 2014-12-27