
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2. Средние величины и показатели вариации. Имеются следующие данные о стаже работы студентов группы заочного отделения ВУЗа (мес.): 26; 63; 94; 16; 49; 14; 78; 10; 130; 20; 86; 29; 75; 22; 32; 21; 96;
|
|
|
|
Имеются следующие данные о стаже работы студентов группы заочного отделения ВУЗа (мес.): 26; 63; 94; 16; 49; 14; 78; 10; 130; 20; 86; 29; 75; 22; 32; 21; 96; 70; 59; 98.
По имеющимся данным по группе из 20 студентов заочного отделения необходимо:
1) построить интервальный ряд распределения признака и его график;
2) рассчитать модальное, медианное и среднее значение, установить его типичность с помощью коэффициентов вариации;
3) проверить распределение на нормальность с помощью коэффициентов асимметрии и эксцесса.
Решение. Для построения интервального ряда из дискретного используется формула Стерджесса, с помощью которой определяется оптимальное количество интервалов (n):
n = 1 +3,322 lg N, (10)
где N – число величин в дискретном ряде.
В нашей задаче n = 1 + 3,322 lg 20 = 1 + 3,322*1,301 = 5,32. Так как число интервалов не может быть дробным, то округлим его до ближайшего целого числа, т.е. до 5.
После определения оптимального количества интервалов определяем размах интервала по формуле:
h = H / n, (11)
где H – размах вариации, определяемый по формуле (12).
H = Хмах –Хmin, (12)
где Xмax и Xmin — максимальное и минимальное значения в совокупности.
В нашей задаче h = (130-10)/5= 24.
Интервальная группировка данных приведена в первом столбце таблицы 1, которая содержит также алгоритм и промежуточные расчеты.
Таблица 1. Вспомогательные расчеты для решения задачи
| Xi, мес. | fi | ХИ | XИfi | ХИ- 
| 
| (ХИ-  )2 )2
| (ХИ-  )2fi )2fi
| (ХИ-  )3 fi )3 fi
| (ХИ-  )4 fi )4 fi
|
| до 34 | -32,4 | 291,6 | 1049,76 | 9447,84 | -306110,016 | 9917964,5184 | |||
| 34-58 | -8,4 | 8,4 | 70,56 | 70,56 | -592,704 | 4978,7136 | |||
| 58-82 | 15,6 | 243,36 | 1216,8 | 18982,08 | 296120,448 | ||||
| 82-106 | 39,6 | 158,4 | 1568,16 | 6272,64 | 248396,544 | 9836503,1424 | |||
| 106-130 | 63,6 | 63,6 | 4044,96 | 4044,96 | 257259,456 | 16361701,4016 | |||
| Итого | — | — | 522,078 | — | 21052,8 | 217935,36 | 36417268,2242 |
На основе этой группировки строится график распределения стажа работы студентов (рис.2).

Рис.2. График распределения стажа работы студентов.
Мода – это наиболее часто повторяющееся значение признака. Для интервального ряда с равными интервалами величина моды определяется по формуле (13):
 , (13)
, (13)
где ХMo – нижнее значение модального интервала; fMo – число наблюдений или объем взвешивающего признака (вес признака) в модальном интервале; fMo-1 – то же для интервала, предшествующего модальному; fMo+1 – то же для интервала, следующего за модальным; h – величина интервала изменения признака в группах.
В нашей задаче чаще всего повторяется (9 раз) первый интервал стаж работы (до 34), значит, это и есть модальный интервал. Используя формулу (13), определяем точное значение модального стажа работы:
Мо = 10 + 24 *(9-0)/(2*9-1-0) = 22,705(мес.).
Медиана – это такое значение признака, которое приходится на середину ранжированного ряда. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака больше медианы, другая – меньше медианы. Для интервального ряда с равными интервалами величина медианы определяется так:
 , (14)
, (14)
где XMe – нижняя граница медианного интервала; h – его величина (размах);  – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; fMe – число наблюдений или объем взвешивающего признака в медианном интервале.
– сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; fMe – число наблюдений или объем взвешивающего признака в медианном интервале.
В нашей задаче второй интервал стажа работы (от 34 до 58) является медианным, так как на него приходится середина ряда распределения стажа работы. Используя формулу (14), определяем точное значение медианного стажа работы:
Ме = 34 + 24*(10-9)/1 = 58 (мес.).
Средняя величина – это обобщающий показатель совокупности, характеризующий уровень изучаемого явления или процесса. Средние величины могут быть простыми и взвешенными. Простая средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном (несгруппированном) порядке, по общей формуле (15). Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием общей формулы (16).
 =
=  ; (15)
; (15)  =
=  . (16)
. (16)
При этом обозначено: Xi – значения отдельных статистических величин или середин группировочных интервалов; m - показатель степени, от значения которого зависят виды средних величин. Используя формулы (15) и (16) при разных показателях степени m, получаем частные формулы каждого вида (см. таблицу 2).
Таблица 2. Виды степенных средних и их применение
| m | Название средней | Формула расчета средней | Когда применяется | |
| простая | взвешенная | |||
| Арифметическая |  = =  (17) (17)
|  = =  (18) (18)
| Чаще всего, кроме тех случаев, когда должны применяться другие виды средних | |
| –1 | Гармоническая |  ГМ = ГМ = 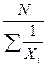 (19) (19)
|  ГМ = ГМ = 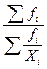 (20) (20)
| Для осреднения величин с дробной размерностью при наличии дополнительных данных по числителю дробной размерности |
| Геометрическая |  (21) (21)
| 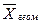 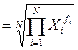 (22) (22)
| Для осреднения цепных индексов динамики | |
| Квадратическая | 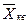 = = 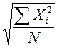 (23) (23)
| 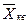 = =  (24) (24)
| Для осреднения вариации признака (расчет средних отклонений) | |
| Кубическая |  = = 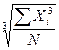 (25) (25)
|  = = 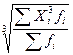 (26) (26)
| Для расчета индексов нищеты населения | |
| Хронологическая |  (27) (27)
|  (28) (28)
| Для осреднения моментных статистических величин |
Выбор вида формулы средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять. Показатель степени m в общей формуле средней величины оказывает существенное влияние на значение средней величины: по мере увеличения степени возрастает и средняя величина (правило мажорантности средних величин), то есть 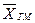 <
<  <
<  <
< 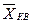 <
<  . Так, если
. Так, если 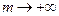 , то
, то  , а если
, а если  , то
, то 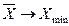 .
.
В нашей задаче, применяя формулу (18) и подставляя вместо  середины интервалов стажа работы ХИ, определяем средний стаж работы студентов:
середины интервалов стажа работы ХИ, определяем средний стаж работы студентов:  = 21088/20 = 54,4 (мес.). Теперь осталось определить типичность или нетипичность найденной средней величины. Это осуществляется с помощью расчета показателей вариации. Чем ближе они к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности. При этом критериальным значением коэффициента вариации служит 1/3.
= 21088/20 = 54,4 (мес.). Теперь осталось определить типичность или нетипичность найденной средней величины. Это осуществляется с помощью расчета показателей вариации. Чем ближе они к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности. При этом критериальным значением коэффициента вариации служит 1/3.
Коэффициенты вариации рассчитываются как отношение среднего отклонения к средней величине. Поскольку среднее отклонение может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации.
Среднее линейное отклонение определяется по формулам (29) и (30):
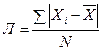 –простое; (29)
–простое; (29) 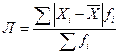 – взвешенное. (30)
– взвешенное. (30)
Среднее квадратическое отклонение определяется как корень квадратный из дисперсии, то есть по формуле (31):
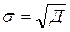 . (31)
. (31)
Дисперсия определяется по формулам (32) или (33):
 –простая; (32)
–простая; (32) 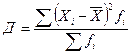 –взвешенная. (33)
–взвешенная. (33)
В нашей задаче, применяя формулу (30), определим ее числитель и внесем в расчетную таблицу. В итоге получим среднее линейное отклонение: Л = 522,078/20 = 26,1039 (мес.). Разделив это значение на средний стаж работы, получим линейный коэффициент вариации: 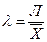 = 26,1039/54,4 = 0,4798. По значению этого коэффициента для рассмотренной группы студентов делаем вывод о типичности среднего стажа работы, т.к. расчетное значение коэффициента вариации превышает критериальное (0,4798 > 0,333).
= 26,1039/54,4 = 0,4798. По значению этого коэффициента для рассмотренной группы студентов делаем вывод о типичности среднего стажа работы, т.к. расчетное значение коэффициента вариации превышает критериальное (0,4798 > 0,333).
Применяя формулу (33), получим в итоге дисперсию: Д = 21052,8/20 = 1052,64. Извлечем из этого числа корень и получим в результате среднее квадратическое отклонение:  =
= 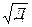 = 32,444 (мес.).Разделив это значение на средний стаж работы, получим квадратический коэффициент вариации:
= 32,444 (мес.).Разделив это значение на средний стаж работы, получим квадратический коэффициент вариации:  = 32,444/54,4 = 0,596. По значению этого коэффициента для рассмотренной группы студентов можно сделать вывод о типичности стажа работы, т.к. расчетное значение коэффициента вариации превышает критериальное (0,596 < 0,333).
= 32,444/54,4 = 0,596. По значению этого коэффициента для рассмотренной группы студентов можно сделать вывод о типичности стажа работы, т.к. расчетное значение коэффициента вариации превышает критериальное (0,596 < 0,333).
В качестве показателей асимметрии используются: коэффициент асимметрии – нормированный момент третьего порядка (34) и коэффициент асимметрии Пирсона (35):
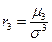 ,(34)
,(34)  .(35)
.(35)
Если значение коэффициента асимметрии положительно, то в ряду преобладают варианты, которые больше средней (правосторонняя скошенность), если отрицательно – левосторонняя скошенность. Если коэффициент асимметрии равен 0, то вариационный ряд симметричен.
В нашей задаче  =
= 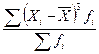 =217935,36/20 = 10896,768;
=217935,36/20 = 10896,768;  =32,4443= 34150,98;
=32,4443= 34150,98;  =10896,768/34150,98 = 0,319 > 0, значит, распределение студентов с правосторонней асимметрией. Это подтверждает и значение коэффициента асимметрии Пирсона: As = (54,4-22,705)/32,444 = 31,695/32,444 = 0,976.
=10896,768/34150,98 = 0,319 > 0, значит, распределение студентов с правосторонней асимметрией. Это подтверждает и значение коэффициента асимметрии Пирсона: As = (54,4-22,705)/32,444 = 31,695/32,444 = 0,976.
Для характеристики крутизны распределения используется центральный момент 4-го порядка:
 =
= 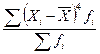 . (36)
. (36)
Для образования безразмерной характеристики определяется нормированный момент 4-го порядка 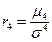 , который и характеризует крутизну (заостренность) графика распределения. При измерении асимметрии эталоном служит нормальное (симметричное) распределение, для которого
, который и характеризует крутизну (заостренность) графика распределения. При измерении асимметрии эталоном служит нормальное (симметричное) распределение, для которого 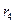 =3. Поэтому для оценки крутизны данного распределения в сравнении с нормальным вычисляется эксцесс распределения (37):
=3. Поэтому для оценки крутизны данного распределения в сравнении с нормальным вычисляется эксцесс распределения (37):
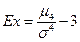 .(37)
.(37)
Для приближенного определения эксцесса может быть использована формула Линдберга (38):
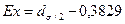 ,(38)
,(38)
где  – доля количества вариант, лежащих в интервале, равном половине
– доля количества вариант, лежащих в интервале, равном половине  (в ту и другую сторону от средней величины).
(в ту и другую сторону от средней величины).
В нашей задаче числитель центрального момента 4-го порядка рассчитан в последнем столбце расчетной таблицы. В итоге по формуле (37) имеем: Ex = (36417268,2242/20)/32,4444–3 =1820863,411 /1107994,414–3 = 1,64338680-3 = -1,356613185. Так как Ex<0, то распределение низковершинное.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 4270; Нарушение авторских прав?; Мы поможем в написании вашей работы!