
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эксперимент 2. Экспериментальная проверка формулы фазовой скорости распространения гидродинамических поверхностных волн 1 страница
|
|
|
|
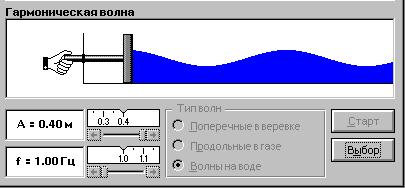
1. Откройте окно «Механические волны» и нажмите кнопку «Тип волн» – «Волны на воде».
2. Выполните измерения аналогичные измерениям п.п. 2-4 эксперимента 1 и запишите результаты измерений и расчётов в табл.4 и 5, аналогичные табл. 2 и 3 эксперимента 1.
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
1. По формуле 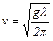 рассчитайте теоретическую фазовую скорость распространения волны для каждой измеренной длины волны и запишите эти значения в табл. 5 в строку vm.
рассчитайте теоретическую фазовую скорость распространения волны для каждой измеренной длины волны и запишите эти значения в табл. 5 в строку vm.
2. Постройте на одном графике зависимости экспериментальной vэ и расчетной vт фазовой скоростей распространения волн от частоты колебаний f.
3. Из полученного графика определите зависимости 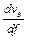 и
и 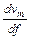 от частоты волны (дисперсию волн).
от частоты волны (дисперсию волн).
4. Сделайте выводы по результатам работы.
Вопросы и задания для самоконтроля
1. Определите, какую волну – продольную или поперечную – описывает уравнение 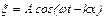 ?
?
2. Что такое фазовая скорость волны? Напишите выражения для фазовой скорости волны.
3. Упругая волна переходит из среды, в которой фазовая скорость равна v в среду, в которой фазовая скорость в два раза больше. Определите, что при этом происходит с длиной волны и частотой?
4. Вдоль оси х распространяется плоская волна с длиной l. Определите наименьшее расстояние между точками среды, в которых колебания совершаются в противофазе.
5. На рис.4 показана «моментальная фотография» смещений частиц среды, в которой распространяется вдоль оси х упругая волна. Укажите направления скоростей частиц в точках А, В и С в случае: а) продольной волны; б) поперечной волны.
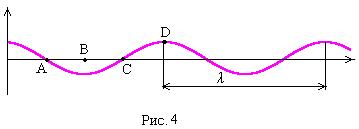
6. На рис.4 показана «моментальная фотография» смещений частиц среды, в которой распространяется вдоль оси х упругая волна. Укажите точки, в которых деформация среды: а) равна нулю; б) принимает максимальное значение. Укажите точки, в которых скорость смещения частиц среды: а) максимальна; б) минимальна.
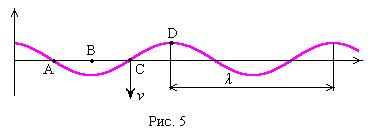
7. В бегущей поперечной волне, показанной на рис.5, частица С имеет направление скорости, указанное на рисунке. Определите: а) какое направление скорости будут иметь частицы А и D в этот момент; б) в каком направлении распространяется волна?
8. Совпадают ли дисперсионные соотношения для бегущих и стоячих волн?
9. Наблюдается ли дисперсия звуковых волн?
10. Что такое волновой пакет?
11. Что такое групповая скорость? Напишите выражение для групповой скорости волн.
12. Морские волны, приближаясь к наклонному берегу, увеличивают свою высоту в несколько раз, а на них образуются пенистые гребни. Объясните это явление.
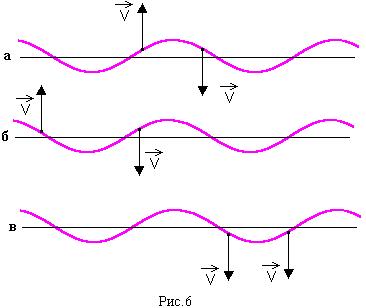
13. На рис.6 а), б), в) показаны направления скоростей двух точек волны. Определите, какие это волны?
14. Вдоль упругого шнура распространяется поперечная волна со скоростью 15 м/с. Период колебаний точек шнура Т = 1,2 с, амплитуда колебаний А = 0,02 м. Определите длину волны, фазу и смещение точки, отстоящей на расстоянии 45 м от источника волн в момент времени t =- 4 с.
15. Волна распространяется от источника колебаний вдоль прямой. Смещение точки для момента времени 0,5 Т составляет 5 см. Точка удалена от источника колебаний на расстояние l/3. Определите амплитуду колебаний.
16. Волны распространяются вдоль шнура со скоростью 3 м/с при частоте 2 Гц. Чему равна разность фаз колебаний двух точек шнура, находящихся на расстоянии 75 см друг от друга?
17. Скорость звука в воде равна 1450 м/с. Определите расстояние между точками, совершающими колебания в противофазах, если частота колебаний 725 Гц.
18. Мимо неподвижного наблюдателя за 10 с прошло 4 гребня волны. Определите период колебаний частиц среды.
19. Разность хода двух когерентных волн с равными амплитудами колебаний равна 15 см, а длина волны 10 см. Определите, каков результат интерференции этих волн?
20. Расстояние между первым и четвёртым узлами стоячей волны равно 24 см. Определите длину бегущей волны.
ЛИТЕРАТУРА

1. Трофимова Т.И. Курс физики. М.: Высшая школа, 2001, Гл.19, §157.
2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2000, Гл.29, §§29.1-29.3.
ЛАБОРАТОРНАЯ РАБОТА 2.10
МОДЕЛИРОВАНИЕ ОПТИЧЕСКИХ СИСТЕМ
Ознакомьтесь с теорией в конспекте и в учебниках: 1. Трофимова Т.И. Курс физики. § 166. 2. Детлаф А.А., Яворский Б.М. Курс физики § 32.7.
Запустите программу «Оптика», «Зрительная труба Кеплера» и «Микроскоп». Нажмите вверху внутренних окон указанных разделов кнопки с изображением страницы. Прочитайте краткие теоретические сведения об этих оптических системах и запишите их в свой конспект.
ЦЕЛЬ РАБОТЫ:
· Ознакомление с оптическими схемами зрительной трубы Кеплера и микроскопа.
· Моделирование этих схем из простых линз.
· Проверка формул увеличения зрительной трубы Кеплера и микроскопа.
КРАТКАЯ ТЕОРИЯ:
1. Зрительная труба Кеплера представляет собой оптическую систему, предназначенную для наблюдения удалённых предметов. Если лучи от предмета приходят в трубу в виде параллельных пучков, то оптическая система трубы называется телескопической.
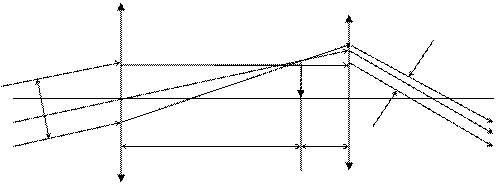
На рис. 1 представлена оптическая схема зрительной трубы Кеплера. Она состоит из длиннофокусного объектива 1 и окуляра 2 – линзы с меньшим фокусным расстоянием.
 2
2
D D¢
G
j y
F1 F2
Рис. 1
Второй главный фокус F1 объектива совпадает с первым главным фокусом F2 окуляра, благодаря чему падающий в объектив параллельный пучок лучей выходит
из окуляра также параллельным пучком. Как показано на рисунке  1, объектив 1 зрительной трубы образует обратное действительное изображение G бесконечно удалённого предмета, которое рассматривается в окуляр 2.
1, объектив 1 зрительной трубы образует обратное действительное изображение G бесконечно удалённого предмета, которое рассматривается в окуляр 2.
Увеличение трубы Г является угловым увеличением и равно отношению
Г = 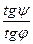 , (1)
, (1)
где y - угол, под которым предмет наблюдается в трубу (согласно правилу знаков, этот угол отрицательный); j - угол, под которым предмет виден невооружённым глазом (если глаз поместить вместо объектива трубы на оптической оси).
Ширина параллельного пучка лучей D, входящих в объектив, обычно равна диаметру объектива. Ширина пучка 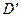 , выходящего из окуляра, определяется диаметром выходного зрачка системы. Выходной зрачок является изображением входного зрачка, даваемого окуляром.
, выходящего из окуляра, определяется диаметром выходного зрачка системы. Выходной зрачок является изображением входного зрачка, даваемого окуляром.
Из рис. 1 имеем для увеличения Г:
Г = - 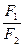 (2), Г = -
(2), Г = - 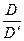 (3)
(3)
Соотношение (2) показывает, во сколько раз увеличиваются угловые размеры изображения в сравнении с угловыми размерами предмета при наблюдении через трубу.
Линейное увеличение b находится по формулам геометрической оптики:
Гb = 1 (4), следовательно b = - 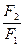 = -
= - 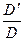 . (5)
. (5)
Так как 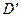 < D, то зрительная труба даёт уменьшение линейных размеров наблюдаемых объектов.
< D, то зрительная труба даёт уменьшение линейных размеров наблюдаемых объектов.
2. Микроскоп предназначен для наблюдения мелких предметов, не различимых глазом. На рис. 2 показана оптическая схема микроскопа.
 1
1
 2
2















1 3
Y 2 F1 F2


 F1 3
F1 3
 -Y¢ 3¢
-Y¢ 3¢

 -Y ¢¢ D 2¢
-Y ¢¢ D 2¢
1¢
d0
Рис. 2
Микроскоп состоит из двух линз: короткофокусного объектива 1 и окуляра 2, фокусное расстояние которого больше, чем у окуляра. Предмет Y располагается вблизи первого фокуса F1 объектива так, что действительное увеличенное обратное изображение - Y¢ получается вблизи первого фокуса F2 окуляра 2 – между ним и окуляром. Окуляр действует как лупа, давая мнимое изображение -U¢¢ на расстоянии наилучшего зрения d0 (d0 = 0,25 м) от глаза 3, который находится непосредственно за окуляром 2. Лучи 1,2,3 позволяют получить изображение -U¢; лучи 1¢, 2¢, 3¢, попадая в систему глаза 3, сходятся на сетчатке глаза, где дают изображение, соответствующее мнимому изображению -U¢¢, даваемому окуляром как лупой. Без участия глаза изображения не видно, а из окуляра выходит расходящийся пучок лучей. Расстояние D между вторым фокусом объектива и первым фокусом окуляра называется оптическим интервалом.
Если предмет Y поместить на расстоянии d1 от объектива микроскопа, его изображение Y´ будет находиться от объектива на расстоянии f1, удовлетворяющем уравнению
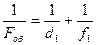 .
.
Изображение предмета будет увеличено при этом в
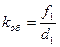 раз. (6)
раз. (6)
Окуляр располагают относительно изображения Y´ так, чтобы оно рассматривалось через него как через лупу. Окончательное изображение Y´´ будет мнимым и будет отстоять от окуляра на расстоянии f2. Если расстояние d2 от окуляра до промежуточного изображения Y´ подобрано так, что оно удовлетворяет уравнению
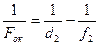 ,
,
то увеличение изображения Y´, даваемое окуляром, при этом окажется равным
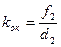 . (7)
. (7)
Увеличение микроскопа Г вычисляется как произведение увеличений объектива и окуляра:
Г = kобkок (8)
В случае, когда F1 и F2 много меньше оптического интервала D, увеличение микроскопа выражается простой формулой: 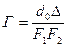 . (9)
. (9)
ИЗМЕРЕНИЯ:
ЭКСПЕРИМЕНТ1. Зрительная труба Кеплера
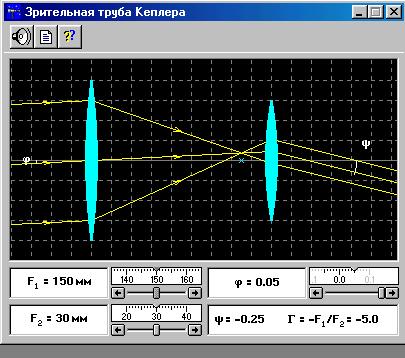
1.Подведите маркер мыши к движку регулятора F1, нажмите левую кнопку мыши и, удерживая её в нажатом состоянии, двигайте движок до установки значения F1, взятого из таблицы 1 для вашей бригады.
2. Установите аналогичным образом F2 и j.
3. Запишите в таблицу 2 значение Гт 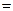
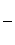
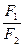 , взятое из нижнего правого окна схемы зрительной трубы Кеплера.
, взятое из нижнего правого окна схемы зрительной трубы Кеплера.
4. С помощью миллиметровой линейки измерьте на экране монитора D и D¢ и запишите эти значения в таблицу 2.
5. Рассчитайте значение Гэ = 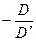 и запишите это значение в таблицу 2.
и запишите это значение в таблицу 2.
6. Сравните полученное значение Гэ со значением Гт.
7. Устанавливая вторые значения F1 и F2, взятые из таблицы 1 для вашей бригады, повторите измерения по п. 2-6, записывая результаты измерений в табл. 2.
8. Оцените абсолютную погрешность измерений.
ТАБЛИЦА 1.
| Бригада | ||||||||
| F1 мм | ||||||||
| F2 мм | ||||||||
| j | 0,00 | 0,01 | 0,02 | 0,03 | -0,01 | -0,02 | -0,03 | -0,04 |
ТАБЛИЦА 2.
| Гт | D мм | D¢мм | Гэ | DГэ |
ЭКСПЕРИМЕНТ 2. Микроскоп.
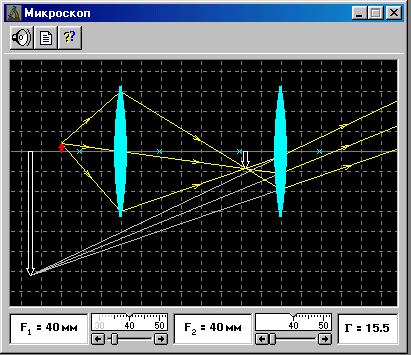
1.Подведите маркер мыши к движку регулятора фокусного расстояния объектива микроскопа, нажмите левую кнопку мыши и, удерживая её в нажатом состоянии, перемещайте движок до установки F1, взятого из таблицы 1 для вашей бригады.
2.Установите аналогичным образом фокусное расстояние окуляра F2 и запишите эти значения в табл. 2.
4. С помощью миллиметровой линейки измерьте расстояния d1, d2, f1, f2 и запишите их в таблицу 2.
5. По формулам (6) и (7) и (8) рассчитайте kоб, kок и Г и запишите эти значения в табл. 2.
4.Рассчитайте по формуле (9) теоретическое значение оптического интервала Dт по параметрам, указанным в нижней части окна.
6.Определите масштаб шкалы окна оптической схемы микроскопа. Для этого измерьте с помощью миллиметровой линейки на экране монитора фокусное расстояние F1 и сопоставьте его со значением, указанным в левом нижнем прямоугольнике окна оптической схемы.
7.Измерьте с помощью миллиметровой линейки на экране монитора оптический интервал микроскопа, приведите его в соответствие с масштабом шкалы окна и запишите полученное значение интервала в табл. 2 (графа Dэ).
8.Сопоставьте полученные экспериментальные значения оптического интервала и увеличения микроскопа с указанными в окошке опыта значениями и сделайте анализ опыта.
9. Сделайте оценку погрешности измерений.
ТАБЛИЦА 1.
| Бригада | ||||||||
| F1 мм | ||||||||
| F2 мм |
ТАБЛИЦА 2.
| F1 мм | F2 мм | d1 мм | d2 мм | f1 мм | f2 мм | kоб | kок | Г | ∆э мм |
Вопросы и задания для самоконтроля
1. Что называется линзой?
2. Какая линза называется тонкой?
3. Что такое главная и побочная оптические оси?
4. Что называется фокусом линзы?
5. Как можно построить изображение произвольной точки в любой линзе?
6. Можно ли с помощью рассеивающей линзы получить увеличенное изображение?
7. Можно ли с помощью собирающей линзы получить уменьшенное изображение предмета?
8. Сформулируйте принцип Ферма.
9. Что называется оптической силой линзы, в каких единицах эта сила измеряется?
10. Запишите формулу тонкой линзы.
11. Назовите аберрации оптических систем.
12. Постройте ход лучей в микроскопе, зрительной трубе Кеплера и фотоаппарате.
13. Какая оптическая система называется телескопической?
ЛАБОРАТОРНАЯ РАБОТА № 2.11
ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА ОТ ОДНОЙ ЩЕЛИ
Ознакомьтесь с теорией в конспекте лекций и в учебниках: 1.Трофимова Т.И. Курс физики. § 179; 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 32, § 32.3.
Запустите программы: «Оптика» и «Дифракция света». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте и запишите краткие теоретические сведения в свой конспект.
ЦЕЛЬ РАБОТЫ:
· Знакомство со схемой дифракции Фраунгофера от одной щели в когерентном свете.
· Определение углов дифракции в параллельных лучах.
КРАТКАЯ ТЕОРИЯ:
Дифракция Фраунгофера наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего  дифракцию. Схема наблюдения дифракции Фраунгофера от одной щели показана на рис. 1.
дифракцию. Схема наблюдения дифракции Фраунгофера от одной щели показана на рис. 1.
 3
3
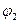 а2
а2
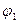 а1
а1
L
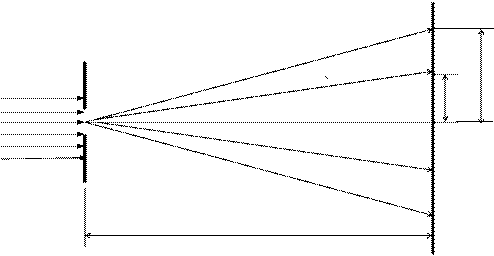
Рис. 1.
Параллельный монохроматический пучок света 1 падает нормально на щель 2, длина которой много больше её ширины d. Согласно принципу Гюйгенса, каждая точка плоскости щели, до которой дошло световое колебание, становится источником вторичных волн, распространяющихся во все стороны под углами дифракции j1, j2,…, т.е. свет дифрагирует при прохождении через щель. Дифрагированные пучки являются когерентными и могут интерферировать при наложении. Результат интерференции в виде полос с периодическим распределением интенсивности наблюдается на экране 3, находящемся на расстоянии L. Условие дифракционного максимума на основе метода зон Френеля определяется формулой
d sin j = ± (2m +1) 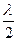 (m = 1,2,…).
(m = 1,2,…).
Более точный расчёт интерференционной картины от одной щели даёт следующие формулы, определяющие углы дифракции, соответствующие дифракционным максимумам:
первого порядка d sin j1 = ± 1,43l;
второго порядка d sin j2 = ± 2,46l; (1)
третьего порядка d sin j3 = ± 3,47l.
Из этих формул, зная ширину щели d и длину волны света l, можно теоретически рассчитать направления на точки экрана, в которых амплитуда, а, следовательно, и интенсивность света максимальна. Аналогичные расчеты можно сделать из экспериментальных данных по измеренным на опыте значениям а1, а2, и а3 и заданному расстоянию между щелью и экраном L:
(для малых углов допускаем: sin a» tg a). Тогда:
sin j 1» 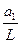 ; sin
; sin 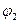 »
» 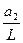 ; sinj3
; sinj3  . (2)
. (2)
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ
Закройте окно теории. Внимательно рассмотрите рисунок, найдите все регуляторы и другие элементы эксперимента и зарисуйте их в конспект. Получите у преподавателя допуск для выполнения лабораторной работы.
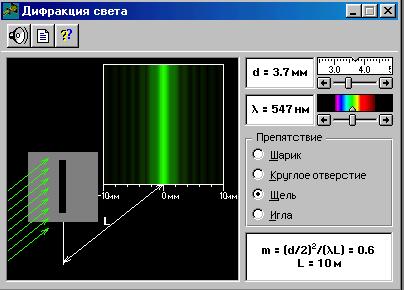
ИЗМЕРЕНИЯ:
1. Подведите маркер мыши к движку регулятора вблизи картинки спектра, нажмите левую кнопку мыши и, удерживая её в нажатом состоянии, двигайте движок до установки значения длины волны l1, взятого из таблицы 1 для вашей бригады.
2. Аналогичным образом, зацепив мышью движок регулятора расстояния между щелями, установите минимальное расстояние d = 2 мм. Измерьте, используя шкалу на экране, расстояние а1 между нулевым и первым максимумами, а2 – между нулевым и вторым максимумами и т. д., до четвёртого максимума. Запишите эти значения в таблицу 2. Увеличивая d на 0,5 мм, проведите эти измерения ещё 4 раза.
3. Согласно таблице 1,устанавливая новые числовые значения длины волны l для вашей бригады, повторите измерения по п.2, записывая результаты измерения в таблицы 3,4,5.
ТАБЛИЦА 1. Значения длины волны l(в нм)
| Бригада | ||||||||
| l1 | 400 | 405 | 410 | 415 | 420 | 425 | 430 | 435 |
| l2 | 500 | 505 | 510 | 515 | 520 | 525 | 530 | 540 |
| l3 | 580 | 585 | 590 | 595 | 600 | 605 | 610 | 615 |
| l4 | 630 | 635 | 640 | 645 | 650 | 655 | 660 | 665 |
ТАБЛИЦЫ 2-5 Результаты измерений при l = ______нм
| d, мм | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
| а1, мм | |||||
| а2, мм | |||||
| а3, мм | |||||
| а4, мм | |||||
| sin j1´103 | |||||
| sin j2´103 | |||||
| sin j3´103 | |||||
| sin j4´103 |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:
1.Измерьте по шкале экрана и внесите в таблицы значения а1, а2, а3, а4.
2. Рассчитайте по формулам (2) и внесите в таблицы значения синусов углов дифракции.
3. Сравните полученные результаты с теоретическими, рассчитанными по формулам (1).
4. Оцените абсолютную ошибку измерений углов дифракции.
5. Проведите качественные наблюдения изменения дифракционной картины при увеличении размера щели от минимального до его максимального значения при неизменной длине волны и запишите результаты этих наблюдений в свой отчёт.
Вопросы и задания для самоконтроля
1. Что называется дифракцией Фраунгофера?
2. Что называется дифракцией Френеля?
3. Что такое световая волна?
4. Что такое зона Френеля?
5. Что такое пятно Пуассона и почему оно возникает?
6. Запишите условия максимумов и минимумов при дифракции Френеля и дифракции Фраунгофера.
7. Решите задачу, предложенную в работе под знаком вопроса в верхней части экрана.
ЛАБОРАТОРНАЯ РАБОТА № 2.12
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Ознакомьтесь с теорией в конспекте и в учебниках: 1. Трофимова Т.И. Курс физики. Гл. 22, §174; 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 31,§ 31.3. Запустите программу «Открытая физика 1.1». Выберите «Оптика» и «Кольца Ньютона». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).
ЦЕЛЬ РАБОТЫ:
· Знакомство с моделированием явления интерференции света в тонких плёнках.
· Изучение интерференции полос равной толщины в схеме колец Ньютона.
· Определение радиуса кривизны линзы.
КРАТКАЯ ТЕОРИЯ:
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1655; Нарушение авторских прав?; Мы поможем в написании вашей работы!