
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эксперимент 2. Экспериментальная проверка формулы фазовой скорости распространения гидродинамических поверхностных волн 3 страница
|
|
|
|
3. По данным, приведённым в табл.3, постройте график зависимости потока вектора напряжённости Ф от расстояния между зарядами d.
4. По построенным графикам сделайте анализ результатов и оцените погрешность проведённых измерений.
Вопросы и задания для самоконтроля
1. Какие поля называют электростатическими?
2. Что такое напряжённость электростатического поля?
3. Как определяется направление вектора напряжённости?
4. Что такое поток вектора напряжённости?
5. Какая линия называется силовой? Почему они не могу пересекаться?
6. Какая линия называется эквипотенциальной?
7. Докажите, что эквипотенциальные и силовые линии ортогональны.
8. От чего зависит густота силовых и эквипотенциальных линий?
9. В чём заключается физический смысл теоремы Остроградского-Гаусса?
10. Рассчитайте, используя теорему О-Г,
а) поле равномерно заряженной бесконечной плоскости;
б) поле двух бесконечных параллельных разноимённо заряженных плоскостей;
в) поле равномерно заряженной сферической поверхности;
г) поле объёмно заряженного шара;
д) поле равномерно заряженного бесконечного цилиндра (нити);
11. Каким образом теорема О-Г и следствия из неё могут быть косвенным подтверждением справедливости закона Кулона?
ЛАБОРАТОРНАЯ РАБОТА № 2.15
ЗАКОН ОМА ДЛЯ НЕОДНООДНОГО УЧАСТКА ЦЕПИ
Ознакомьтесь с теорией в конспекте и учебниках: 1. Трофимова Т.И. Курс физики. Гл. 12, §100. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 19, §19.1. Запустите программу «Электричество и магнетизм». Выберите: «Цепи постоянного тока». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).
ЦЕЛЬ РАБОТЫ:
· Знакомство с компьютерным моделированием цепей постоянного тока.
· Экспериментальное подтверждение закона Ома для неоднородного участка цепи.
КРАТКАЯ ТЕОРИЯ:
ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ (СИЛЫ) ТОКА  .
.
ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ: величина (сила) тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения U на проводнике 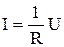 , где R - сопротивление проводника.
, где R - сопротивление проводника.
РЕЗИСТОРОМ называется устройство, обладающее заданным постоянным сопротивлением.
РЕОСТАТОМ называется переменное сопротивление.
НАПРЯЖЕНИЕМ НА УЧАСТКЕ ЦЕПИ 1-2 называется физическая величина, определяемая выражением
U12 = j1-j2+E12.
ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ:
 , где j1 и j2 - потенциалы концов участка, Е12 - э.д.с., действующая на данном участке цепи.
, где j1 и j2 - потенциалы концов участка, Е12 - э.д.с., действующая на данном участке цепи.
Применяя закон Ома для неоднородного участка цепи, необходимо помнить о правиле выбора знаков: произведение IR следует брать со знаком «+», если направление обхода совпадает с направлением тока на этом участке, э.д.с. Е12 будет иметь знак «+», если её направление (от минуса к плюсу) совпадает с направлением обхода. При этом надо иметь в виду, что вольтметр, подключённый к концам любого участка цепи, будет показывать разность потенциалов между точками подключения прибора, а направление отклонения стрелки прибора будет определяться параметрами внешней цепи.
Таким образом, закон Ома для полной цепи можно записать в виде
 (1)
(1)
Из формулы (1) видно, что при I = 0 вольтметр покажет э.д.с. источника, включённого в данный участок цепи.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
В данной лабораторной работе изучается модель электрической цепи, содержащей на одном из своих участков источник электродвижущей силы (э.д.с.). На этом участке, в зависимости от соотношений между параметрами цепи, разность потенциалов между его крайними точками может менять знак, переходя через 0.
ИЗМЕРЕНИЯ:
Соберите на экране опыта замкнутую цепь, показанную на рис.1.

Рис.1.
Для этого сначала щелкните левой кнопкой мыши на кнопке э.д.с.  в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где должен быть расположен источник э.д.с.
в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где должен быть расположен источник э.д.с.
Разместите далее последовательно с источником резисторы, выполняющие функции его внутреннего сопротивления r и сопротивления неоднородного участка R1 (нажав предварительно кнопку  в нижней части экрана), и амперметр (кнопка
в нижней части экрана), и амперметр (кнопка  там же). Затем расположите резистор нагрузки (реостат) и последовательно соединенный с ним амперметр. Над участком цепи расположите вольтметр
там же). Затем расположите резистор нагрузки (реостат) и последовательно соединенный с ним амперметр. Над участком цепи расположите вольтметр  , измеряющий разность потенциалов на этом неоднородном участке цепи.
, измеряющий разность потенциалов на этом неоднородном участке цепи.
Соедините все указанные приборы в замкнутую цепь. Для этого нажмите кнопку соединительного провода  внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в необходимых местах рабочей зоны и сформируйте замкнутую цепь, показанную на рис. 1.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в необходимых местах рабочей зоны и сформируйте замкнутую цепь, показанную на рис. 1.
Установите заданные значения параметров для каждого прибора цепи. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой  . Затем щелкните на данном приборе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, установите значения R1, r, E, которые указаны в таблице 1 для вашей бригады.
. Затем щелкните на данном приборе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, установите значения R1, r, E, которые указаны в таблице 1 для вашей бригады.
Установите сопротивление реостата R = 1 Ом. Измерьте значения тока и разности потенциалов (щелкнув мышью по кнопке «Счет») и запишите их в таблицу 2.
Увеличивая сопротивление реостата R каждый раз на 1Ом, повторите измерения силы тока и разности потенциалов по п.5 и заполните таблицу 2.
Включите в схему второй источник питания, как показано на рис.2, и установите значение Е2, соответствующее номеру вашей бригады.
Проведите на второй схеме все измерения п.п. 5,6.
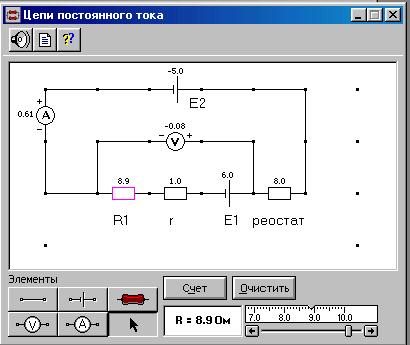
Рис.2
Таблица 1. Значения э.д.с. (E1и Е2), внутреннего сопротивления
источника (r) и R1
| Бригада | ||||||||
| E1, В | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 |
| Е2,В | -2,5 | -3,5 | -4,0 | -3,5 | -3,0 | -4,5 | -5,0 | -5,5 |
| r, Ом | 1,0 | 1,2 | `1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 |
| R1, Ом | 8,0 | 7,5 | 7,0 | 6,5 | 8,5 | 9,0 | 9,5 | 10,0 |
Таблица 2. Результаты измерений
| Номер измерения | E1=___ R1 =__ r =___ | E1=__ E2=__ R1 =__ r =__ | ||||
| R Ом | U В | I А | R Ом | U В | I А | |
| … | ||||||
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:
На одном графике покажите зависимость показаний вольтметра (ось ординат) от силы тока для первой и второй схем (ось абсцисс).
Экстраполируя оба графика до пересечения с осью ординат, определите по формуле (1) экспериментально установленное значение э.д.с. (Е1) источника тока, включённого в неоднородный участок цепи, и сравните его с установочным значением.
По тангенсу наклона прямой к оси I определите полное сопротивление участка для двух схем и сравните его значение с установочным.
Рассчитайте погрешности измерений и запишите окончательный результат.
Вопросы и задания для самоконтроля
1.Дайте определения понятий: разность потенциалов, э.д.с. источника тока, напряжение на участке цепи.
2.Что называется сторонней силой? Какова её природа?
3.Укажите правильное выражение закона Ома для неоднородного участка цепи, показанного на рисунке:

1 2 j1 - j2 = 2В
R Е = 6В
1) IR = (j1-j2) +E; 2) IR = (j1-j2) - E; 3) IR = E -(j1-j2); 4) IR = E;
= (j1-j2).
4.Выведите Закон Ома в дифференциальной форме.
5.Что называется удельным сопротивлением проводника? От чего оно зависит?
6.Сформулируйте правила Кирхгофа для разветвлённых цепей.
7.Выведите формулы сопротивлений батарей последовательно и параллельно соединённых резисторов.
8.Сформулируйте закон Ома для полной цепи.
9.Объясните принцип действия экспериментальной установки. В чём принципиальная разница первого и второго варианта схем?
ЛАБОРАТОРНАЯ РАБОТА № 2.16
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЧАСТИЦЫ МЕТОДОМ ОТКЛОНЕНИЯ В МАГНИТНОМ ПОЛЕ
Ознакомьтесь с теорией в конспекте и учебниках: 1. Трофимова Т.И. Курс физики. Гл. 14, §115. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 23, §23.3.Запустите программу «Электричество и магнетизм». Выберите: «Масс-спектрометр». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).
ЦЕЛЬ РАБОТЫ:
· Знакомство с компьютерным моделированием движения заряженных частиц в магнитном поле.
· Ознакомление с принципом работы масс-спектрометра.
· Определение удельного заряда частиц.
КРАТКАЯ ТЕОРИЯ:
1. СИЛА ЛОРЕНЦА- сила, действующая на движущуюся со скоростью v в однородном магнитном поле с индукцией В частицу с зарядом q:
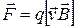
 (1)
(1)
Модуль этой силы равен
 , (2)
, (2)
где a- угол между векторами  и
и 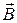 . Сила Лоренца направлена перпендикулярно скорости частицы, сообщает ей только нормальное ускорение и вызывает искривление траектории частицы.
. Сила Лоренца направлена перпендикулярно скорости частицы, сообщает ей только нормальное ускорение и вызывает искривление траектории частицы.
Если частица влетает в однородное магнитное поле в направлении, перпендикулярном линиям магнитной индукции, то частица будет двигаться по дуге окружности, плоскость которой перпендикулярна линиям индукции. Радиус окружности можно найти из второго закона динамики:
 . (3)
. (3)
УДЕЛЬНЫМ ЗАРЯДОМ ЧАСТИЦЫ называется отношение заряда частицы к её массе. Тогда из формулы (3) удельный заряд будет равен:
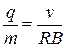 . (4)
. (4)
Период обращения частицы 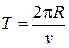 равен
равен
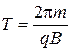 , (5)
, (5)
и не зависит от скорости.
МАСС-СПЕКТРОМЕТРОМ называется прибор, для разделения ионизованных молекул и атомов (изотопов) по их массам, основанный на воздействии электрических и магнитных полей на пучки ионов, летящих в вакууме.
Простейшая модель масс-спектрографа показана на рис. 1.

Рис. 1.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
1.Подведите маркер мыши к движку регулятора величины магнитной индукции, нажмите левую кнопку мыши и, удерживая ее в нажатом состоянии, двигайте движок, установив числовое значение В, взятое из таблицы 1 для вашей бригады.
2. Аналогичным образом, зацепив мышью движок регулятора скорости, установите минимальное значение 103 м/с.
3. Нажмите мышью кнопку «Изотопы С12-С14»
4. Нажмите мышью кнопку «Старт» и синхронно секундомер. Проследите за движением двух изотопов в магнитном поле модельного масс-спектрометра и по секундомеру определите время этого движения.
5. Запишите в таблицу 2 значения радиусов окружностей, по которым двигались эти изотопы (они показаны красным и синим цветом в правом углу окна) и время движения изотопов в вакуумной камере масс-спектрометра.
6. Последовательно увеличивая скорость частиц на 103м/с, проделайте п.п.4-5 ещё 9 раз и заполните таблицу 2.
7. Нажмите мышью кнопку «Изотопы Ne20-Ne22», проведите измерения п.п.4-6 и заполните таблицу 3.
8. Проведите аналогичные измерения с изотопами урана и неизвестного химического элемента и заполните таблицы 4 и 5.
Таблица 1. Значения магнитной индукции В
| Номер бригады | ||||||||
| В, мТл (табл.2,3) | ||||||||
| В, мТл (табл.4,5) | 9,0 | 9,1 | 9,2 | 9,3 | 9,4 | 9,5 | 9,6 | 9,7 |
Таблицы 2-5. Результаты измерений и расчётов
В = _______
| v×103,м/с | ||||||||||
| R1, см | ||||||||||
| R2, см | ||||||||||
| Т1/2, с | ||||||||||
| q1/m1, Кл/кг q2/m2, Кл/кг | ||||||||||
| Табличные значения: q1/m1 = q2/m2= |
ОБРАБОТК РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:
1. Вычислите по формуле (4) удельные заряды изотопов углерода, неона, урана и неизвестного химического элемента и запишите полученные значения в соответствующие таблицы.
2. Используя справочные материалы по физике и химии, определите табличные значения удельных зарядов исследованных изотопов и сравните их с полученными в опыте.
3. Постройте график зависимости времени пролёта изотопов в камере масс-спектрометра от их скорости и сделайте выводы по результатам анализа этого графика.
4. Проведите оценку погрешностей проведённых измерений.
ПОЛЕЗНЫЕ СВЕДЕНИЯ:
Атомная единица массы (а.е.м.) = 1,660×10-27 кг.
Элементарный заряд е = 1,602×10-19 Кл.
Вопросы и задания для самоконтроля
1. Как определяется направление действия силы Лоренца?
2. Почему сила Лоренца не совершает работы?
3. Как будет двигаться заряженная частица в магнитном поле, если угол a между векторами 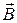 и
и  меньше p/2?
меньше p/2?
4. Ионы двух изотопов с массами m1 и m2 , имеющие одинаковый заряд и прошедшие в электрическом поле одинаковую ускоряющую разность потенциалов, влетают в магнитное поле перпендикулярно силовым линиям магнитного поля. Найдите отношение радиусов окружностей, по которым будут двигаться ионы в магнитном поле.
5. Определите, во сколько раз изменится радиус окружности, по которой заряженная частица движется в однородном магнитном поле, если её кинетическую энергию увеличить в n раз?
6. Определите удельный заряд иона, который в масс-спектрометре совершает один оборот за 628 мкс в однородном магнитном поле с индукцией 50 мТл.
7. Пучок ионов, влетающих в вакуумную камеру масс-спектрометра перпендикулярно силовым линиям однородного магнитного поля, расщепляется (рис.2). Определите, какая траектория соответствует: а) большему импульсу,

Рис.2
если ионы имеют одинаковые заряды, но разные импульсы; б) большему заряду, если частицы имеют одинаковые импульсы, но разные заряды?
8. Два электрона движутся в одном и том же однородном магнитном поле по орбитам с радиусами R1 R2 (R1> R2). Сравните их угловые скорости.
9. В однородном магнитном поле движутся по окружностям протон и a-частица, имея равные кинетические энергии. Какая из этих частиц будет иметь орбитальный магнитный момент и период вращения больше и во сколько раз?
10. Заряженная частица влетела в однородное магнитное поле под углом a < p/2 между векторами 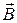 и
и  . Определите, отличны ли от нуля тангенциальная и нормальная составляющие ускорения частицы?
. Определите, отличны ли от нуля тангенциальная и нормальная составляющие ускорения частицы?
11. Заряженная частица летит прямолинейно и равномерно в однородном электромагнитном поле, представленном суперпозицией взаимно перпендикулярных электрических (напряжённостью Е) и магнитных (индукцией В) полей. Найдите скорость движения частицы.
12. Заряженная частица вращается в однородном магнитном поле с индукцией В по окружности радиуса R. Параллельно магнитному полю возбуждается электрическое поле напряжённостью Е. Определите, сколько времени должно действовать электрическое поле, чтобы кинетическая энергия частицы возросла в два раза?
ЛАБОРАТОРНАЯ РАБОТА № 2.17
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ ПОСТОЯННОГО ТОКА С КОНДЕНСАТОРОМ
Ознакомьтесь с теорией в конспекте и в учебниках 1. Трофимова Т.И. Курс физики. Гл.11, §94. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл.16, §16.3. Выберите: «ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ» и «Конденсаторы в цепях постоянного тока». Нажмите кнопку с изображением страницы во внутреннем окне. Прочитайте теорию и запишите основные сведения в свой конспект лабораторной работы. Закройте окно теории, нажав кнопку с крестом в правом верхнем углу внутреннего окна.
ЦЕЛЬ РАБОТЫ:
· Знакомство с компьютерным моделированием переходных процессов в цепях постоянного тока.
· Проверка закона сохранения энергии в цепях постоянного тока с конденсатором.
· Определение ёмкости конденсатора методом разрядки.
КРАТКАЯ ТЕОРИЯ:
ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными
РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи
IR=U,
где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что 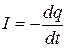 и
и  , преобразуем закон Ома к виду
, преобразуем закон Ома к виду
 (1)
(1)
В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем
 , (2)
, (2)
где q0 - начальный заряд конденсатора, е - основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t. Продифференцировав выражение (2) по времени, найдём закон изменения тока:
 , (3)
, (3)
где I0 - сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.
Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:
 (4)
(4)
ЗАРЯДКА КОНДЕСАТОРА.
Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи:
 .
.
После разделения переменных уравнение примет вид:

Проинтегрировав это уравнение с учётом начального условия
q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим
 , или после потенцирования
, или после потенцирования
q = 
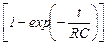 . (4)
. (4)
Анализ этого выражения показывает, что заряд приближается к своему максимальному значению, равному С 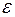 , асимптотически при t ® ¥.
, асимптотически при t ® ¥.
Подставляя в формулу (4) функцию I(t) = dq/dt, получим
 . (5)
. (5)
Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dАист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW:
dAист= dQ + dW,
где dAист = 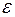 Idt, dQ =I2Rdt, dW =d
Idt, dQ =I2Rdt, dW =d  . Тогда для произвольного момента времени t имеем:
. Тогда для произвольного момента времени t имеем:
Аист(t)=  =
= 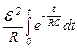 =С
=С 
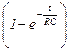 . (6)
. (6)
Q(t)=  =С
=С 
 .(7)
.(7)
W(t) = 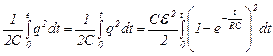 =
=  . (8)
. (8)
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
В реальных электрических цепях постоянного тока, содержащих конденсаторы, переходные процессы разрядки и зарядки конденсаторов проходят за время порядка 10–6 – 10-3 с. Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 1478; Нарушение авторских прав?; Мы поможем в написании вашей работы!