Эксперимент 2. Экспериментальная проверка формулы фазовой скорости распространения гидродинамических поверхностных волн 2 страница

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.1).

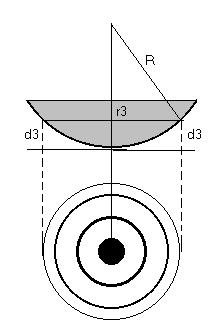
Рис.1

Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней поверхностей воздушной прослойки, будут интерферировать между собой. При этом образуются интерференционные полосы, имеющие форму концентрических светлых и тёмных колец, убывающей ширины.

В отражённом свете оптическая разность хода с учётом потери полуволны будет равна

, (1)

где d- толщина воздушного зазора. Из рис.1 следует, что

. (2)

Учитывая, что d² является величиной второго порядка малости, то из (2) получим . (3)

Следовательно,

. (4)

В точках, для которых оптическая разность хода равна

, (5)

возникают тёмные кольца. Из формул (4) и (5) радиус k-ого тёмного кольца будет равен

(6)

Формула (6) позволяет определить радиус кривизны линзы

.

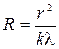Вследствие деформации стекла, а также наличия на стекле пылинок невозможно добиться плотного примыкания линзы и пластины в одной точке. Поэтому при определении радиуса кривизны линзы пользуются другой формулой, в которую входит комбинация из двух значений радиусов интерференционных колец r_m и r_n, что позволяет исключить возможный зазор в точке контакта линзы и стеклянной пластины:

. (7)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

1. Внимательно рассмотрите окно опыта, показанное на рисунке 2, и зарисуйте необходимое в свой конспект лабораторной работы.

2. Зацепите мышью движок регулятора длины волны монохроматического света и установите первое значение длины волны из таблицы 1 для вашей бригады. Аналогичным образом установите первое значение радиуса кривизны линзы R.

ВНИМАНИЕ! Цель работы - проверить соответствие установочного значения радиуса кривизны линзы и рассчитанного по формуле (7).

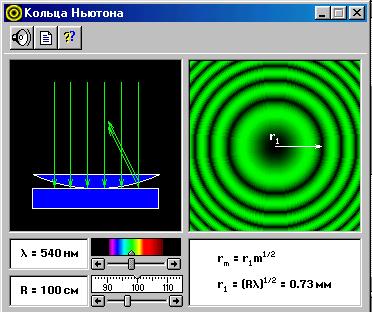
Рис.2

3. По формуле и указанному значению r ₁ в правом нижнем прямоугольнике окна опыта рассчитайте значения радиусов 3, 4, 5 и 6-ого тёмных колец Ньютона и запишите эти значения в таблицу 2.

4. По формуле (7) для m₁ = 3 и n₁ = 5 и m₂ = 4 и n₂ = 6 рассчитайте радиусы кривизны линзы R^*₁ и R^*₂ и запишите эти значения в табл.2.

5. Установите мышью вторые значения радиуса кривизны линзы и длины волны из таблицы 1 и выполните измерения п.п. 3 и 4.

6. Проанализируйте полученные результаты и оцените погрешность проведённых измерений.

Таблица 1. Значения длины волны и радиуса кривизны линзы.

Бригады	l1, нм	l2, нм	R1, см	R2, см
1,5
2,6
3,7
4,8

Таблица 2. Результаты измерений и расчетов.

l1= _____ R1 = _____	l2 = ____ R2 = _____
r3	r5	r4	r6	r3	r5	r4	r6
=	=	=	=

Вопросы и задания для самоконтроля

1. Что такое полосы равной толщины и равного наклона? Где они локализованы?

2. Проведите расчёт интерференционной картины в тонкой плёнке.

3. Что называется временем когерентности немонохроматической волны?

4. Что называется длиной когерентности?

5. Почему для немонохроматического света число видимых интерференционных колец будет ограниченным? От чего будет зависеть это число?

6. Объясните, почему расстояние между кольцами изменяется с изменением радиуса кривизны линзы при неизменной длине волны?

7. Как изменится картина колец Ньютона, если воздушный зазор между линзой и пластиной заполнить водой?

8. Почему в отражённом свете в центре наблюдается тёмное кольцо?

9. Как изменится картина колец Ньютона, если наблюдение проводить в проходящем свете?

10. Почему масляное пятно на поверхности жидкости имеет радужную окраску?

11. Объясните, как явление интерференции света в тонких плёнках используется для просветления оптики?

ЛАБОРАТОРНАЯ РАБОТА № 2.13

ИССЛЕДОВНИЕ ЗАВИСИМОСТИ МОЩНОСТИ И К.П.Д. ИСТОЧНИКА ПОСТОЯННОГО ТОКА ОТ ВНЕШНЕЙ НАГРУЗКИ

Ознакомьтесь с теорией в конспекте и учебниках: 1. Трофимова Т.И. Курс физики. Гл. 12, §99. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 19, §19.2.Запустите программу «Электричество и магнетизм». Выберите: «Цепи постоянного тока». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).

ЦЕЛЬ РАБОТЫ:

· Знакомство с компьютерным моделированием цепей постоянного тока.

· Исследование зависимости мощности и к.п.д. источника постоянного тока от сопротивления внешней цепи.

КРАТКАЯ ТЕОРИЯ:

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:

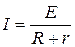, (1)

I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.

МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ:

. (2)

Из формулы (2) видно, что при коротком замыкании цепи (R ®0) и при R ® эта мощность равна нулю. При всех других конечных значениях R мощность Р ₁> 0. Следовательно, функция Р ₁ имеет максимум. Значение R ₀, соответствующее максимальной мощности, можно получить, дифференцируя Р₁ по R и приравнивая первую производную к нулю:

. (3)

Из формулы (3), с учётом того, что R и r всегда положительны, а Е ¹ 0, после несложных алгебраических преобразований получим:

R₀ = r. (4)

Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.

При этом сила тока в цепи (5)

равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного

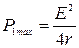. (6)

Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна

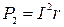. (7)

Следовательно, полная мощность, выделяемая во всей цепи, определится формулой

= I² (R+r) = IE (8)

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен

. (9)

Из формулы (8) следует, что

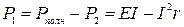, (10)

т.е. Р ₁ изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при . Первое значение соответствует разомкнутой цепи (R>> r), второе – короткому замыканию (R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид

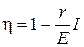(11)

Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи (I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.

Зависимость мощностей Р₁, Р_полн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.

Рис.1. I ₀ E/r

Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р₁, достигает наибольшего значения, к.п.д. в этот момент равен 50%.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Рис. 2.

Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.

Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку в нижней части экрана) и амперметр (кнопка там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр , измеряющий напряжение на нагрузке.

Подключите соединительные провода. Для этого нажмите кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.

4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашей бригады.

Таблица 1. Исходные параметры электрической цепи

Номер бригады
Е, В	10,0	9,5	9,0	8,5	8,0	8,5	9,0	9,5
r, Ом	4,8	5,7	6,6	7,5	6,4	7,3	8,2	9,1

5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.

6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.

7. Вычислите по формулам (2), (7), (8), (9) Р₁, Р₂, Р_полн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.

8. Постройте на одном листе миллиметровой бумаге графики зависимости P₁ = f(R), P₂ = f(R), P_полн=f(R), h = f (R) и U = f(R).

9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.

Таблица 2. Результаты измерений и расчётов

R, Ом	2,0	2,5	3,0	…
U, В
I, А
P1, Вт
P2, ВТ
Pполн, ВТ
h

Вопросы и задания для самоконтроля

1. Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.

2. Что такое ток короткого замыкания?

3. Что такое полная мощность?

4. Как вычисляется к.п.д. источника тока?

5. Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.

6. Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?

7. К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.

8. Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.

9. Объясните явление.

10.При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.

ЛАБОРАТОРНАЯ РАБОТА № 2.14

ТЕОРЕМА ОСТРОГРАДСКОГО -ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ВАКУУМЕ

Ознакомьтесь с теорией в конспекте и в учебниках: 1. Трофимова Т.И. Курс физики. Гл. 11, §81,82; 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 14,§ 14.1, 14.2. Запустите программу «Открытая физика 1.1». Выберите «Электричество и магнетизм» и «Электрическое поле точечного заряда». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).

ЦЕЛЬ РАБОТЫ:

· Знакомство с графическим моделированием электростатических полей.

· Экспериментальная проверка теоремы Остроградского-Гаусса.

· Экспериментальное определение величины электрической постоянной.

КРАТКАЯ ТЕОРИЯ:

НАПРЯЖЁННОСТЬ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ в данной точке есть векторная физическая величина, равная отношению силы 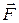, действующей со стороны поля на неподвижный точечный заряд q₀, помещённый в данную точку поля, к величине этого заряда:

.

ЛИНИЯМИ НАПРЯЖЁННОСТИ (силовыми линиями) называются линии, проведённые в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором напряжённости. Линии напряжённости проводят так, что они начинаются на положительных зарядах и оканчиваются на отрицательных или уходят в бесконечность. (Рис. 1)

а) б)

Рис.1. Линии напряжённости двух точечных зарядов: а) разноимённых;

б) одноимённых

ПРИНЦИП СУПРПОЗИЦИИ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ: напряжённость электростатического поля систем точечных зарядов равна векторной сумме напряжённостей полей каждого из этих зарядов в отдельности:

.

ПОТОК ВЕКТОРА НАПРЯЖЁННОСТИ.

Силовая линия, определяя направление вектора напряжённости, сама по себе не определяет величину модуля вектора напряжённости. Введём условие, связывающее величину модуля вектора напряжённости с числом проводимых линий напряжённости через единицу площади. Для этого выделим в электростатическом поле малую область, в пределах которой электростатическое поле можно считать однородным. Проведём в этой области элементарную площадку , перпендикулярную к линиям напряжённости. Условимся через эту площадку проводить такое число линий напряжённости, чтобы число линий, приходящихся на единицу поверхности площадки , равнялось величине модуля вектора напряжённости в области этой площадки, т.е. потребуем выполнения условия:

. (1)

При выполнении этого условия графического изображения электростатических полей численное значение вектора напряжённости будет связано с густотой линий напряжённости. Тогда число линий напряжённости, пронизывающих элементарную площадку dS, нормаль которой образует угол a с вектором , равно

, (2)

где величина dФ называется потоком вектора напряжённости через площадку dS. Число линий напряжённости Ф, пронизывающих некоторую поверхность S, назовём потоком вектора напряжённости через эту поверхность. Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность будет равен

. (3)

Для замкнутой поверхности принято считать положительным направление нормали к элементу поверхности, выходящее из объёма, ограничиваемого поверхностью. Тогда линии напряжённости, выходящие из объёма, создадут положительный поток Ф₊, линии, входящие в объём, создадут отрицательный поток Ф_-, а результирующий поток будет равен алгебраической сумме этих потоков.

ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА: поток вектора напряжённости электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на e₀.

Ф₊ + Ф _- = (4)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Рассмотрите внимательно схему опыта и зарисуйте необходимое в свой конспект лабораторной работы.

Рис. 2

Как известно, электростатическое поле в вакууме изотропное. Следовательно, количество силовых линий, пересекающих произвольную замкнутую поверхность, содержащую внутри себя электрические заряды, будет пропорционально количеству силовых линий, пересекающих замкнутый контур, ограничивающий площадь сечения, в которой находятся электрические заряды этой замкнутой поверхности.

Такое допущение даёт возможность привести в количественное соответствие реальное трёхмерное электростатическое поле с его графической интерпретацией в плоской компьютерной модели, которая показана на рис. 2. Для этого определим число силовых линий Ф, которые фактически должны пересекать произвольную замкнутую поверхность, внутри которой находится электрический заряд q = 1мкКл. По теореме Остроградского-Гаусса имеем:

.

Откройте окно опыта. В нижнем правом прямоугольнике «Конфигурация» щёлкните мышью на кнопке «Один заряд». Зацепив мышью, перемещайте движок регулятора величины заряда и установите значение q ₁ = +1мкКл. Подсчитайте число силовых линий, выходящих из заряда. Их должно быть 6. Следовательно, силовая линия в плоской компьютерной модели опыта соответствует

N = (5)

линиям реального трёхмерного кулоновского поля. На основании таких допущений и оценок создаётся возможность экспериментальной проверки теоремы Остроградского-Гаусса с помощью графического компьютерного моделирования электростатических полей в данной лабораторной работе.

ЭКСПЕРИМЕНТ 1. (Постоянное пространственное распределение переменного заряда внутри замкнутой поверхности)

1. В нижнем правом прямоугольнике «Конфигурация» нажмите мышью кнопку «Два заряда».

2. Зацепив мышью, перемещайте движок регулятора первого заряда до установления значения, указанного в табл. 1 для вашей бригады.

3. Аналогичным образом установите заданное в табл.1 расстояние d между зарядами.

4. Установите мышью на кнопке «Силовые линии» флажок.

5. Установите величину второго заряда 0 и подсчитайте число силовых линий Ф ₊ выходящих и Ф _- входящих через границы замкнутого контура, которым в нашем опыте будет являться прямоугольная рамка окна опыта. При этом внимательно смотрите за направлением стрелок на силовых линиях поля. Запишите эти данные и разность Ф = Ф₊ - Ф _- в таблицу 2.

6. Последовательно устанавливайте заряды: q₂ = +1, +2, +3, +4, +5мкКл и выполните п.5 ещё 5 раз.

ЭКСПЕРИМЕНТ 2.( Переменное пространственное распределение постоянного заряда внутри замкнутой поверхности)

1. Установите значения q₁ и q₂ соответствующие значениям, указанным в таблице 1 для вашей бригады.

2. Установите также минимальное расстояние между зарядами d = 2м и на экране окна эксперимента, подсчётом определите числа Ф ₊, Ф _- и Ф.

3. Последовательно увеличивая расстояние между зарядами с шагом 0,5м, выполните п. 2 ещё 6 раз.

4. Результаты измерений запишите в табл. 3.

Таблица 1. Установочные значения физических параметров для проведения экспериментов

Бригады
ЭКСПЕРИМЕНТ 1
q1,мкКл	-1	-2	-3	-4	-5	-4	-3	-2
d, м
ЭКСПЕРИМЕНТ 2
q1,мкКл	-5	-5	-5	-5	-5	-4	-4	-4
q2,мкКл	+1	+2	+3	+4	+5	+4	+3	+2

Таблица 2. Результаты измерений в эксперименте 1

q₁ = _____ d =_____

q2 = 0 мкКЛ

q2 = +1 мкКЛ

q2 = +2 мкКЛ

q2 = +3 мкКЛ

q2 = +4 мкКЛ

q2 = +5 мкКЛ

Ф +

Ф-

Ф

Ф +

Ф-

Ф

Ф +

Ф-

Ф

Ф +

Ф-

Ф

Ф +

Ф-

Ф

Ф +

Ф-

Ф

Таблица 3. Результаты измерений в эксперименте 2.

q₁ = _____ q₂ = ______

d =2м

d = 3м

d = 4м

d = 5м

d =4,5 м

d =3,5 м

Ф+

Ф-

Ф

Ф+

Ф-

Ф

Ф+

Ф-

Ф

Ф+

Ф-

Ф

Ф+

Ф-

Ф

Ф+

Ф-

Ф

ОБРАБОТКА РЕЗУЛ ЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА

1. Постройте по данным табл.2 график зависимости потока вектора напряжённости Ф от величины заряда q.

2. По котангенсу угла наклона графика и используя ф-лы (4) и (5), определите электрическую постоянную e₀ .

Дата добавления: 2014-12-23