Стійкість комп’ютерної моделі

Наступне дослідження стосується прийнятних значень проміжків часу Δ t. Про це вже йшлося в задачі про чутки на с. 56 (п. 2.3).

Надамо інтервалові часу Δ t більшого значення, ніж у попередньому досліді. Нехай Δ t = 0,5. Поясніть причину спостережуваної зміни у таблиці та на відповідному графіку.

Продовжимо далі збільшення інтервалів Δ t, надаючи їм послідовних зростаючих значень Δ t = 1; Δ t = 1,1;... (рис. 4.8).

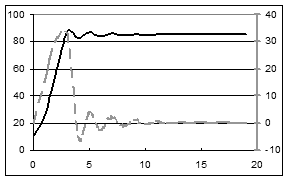
Рис. 4.8

Як віднестися до отриманого результату? Його прийняття означатиме, що значення проміжків часу Δ t здатні впливати на хід процесів, але з іншого боку рис. 4.8 з’явився з тієї самої моделі, що й рис. 4.7. Якому ж із цих результатів надати перевагу? Весь наш життєвий досвід і досвід навчальної діяльності свідчать, що перебіг природних процесів не може залежати, наприклад, від того, якою стрілкою годинника ми користуємось: хвилинною чи секундною. Насправді, рис. 4.8 ілюструє, що відбувається, коли модель і обчислювальний алгоритм втрачають адекватність.

Непорозуміння в таблиці (а отже й на графіку) продовжуються і при ще більшому значенні Δ t = 1,5 (перевірте). Вони набувають стійкого характеру, і тому виникає природне питання: яке відношення до досліджуваної системи мають всі ці результати?

В комп’ютерному моделюванні такі ситуації добре відомі. Справа в тому, що, коли до процесу розв’язування задач залучається комп’ютер – пристрій, що працює за дискретним принципом, – то при побудові комп’ютерної математичної моделі завжди виникає необхідність замінювати неперервні в часі процеси на їхні дискретні аналоги. Зрозуміло, що математична модель може бути як неперервною, так і дискретною, тоді як комп’ютерна модель завжди дискретна. Рівень дискретизації може бути різним: зменшення кроку дискретизації наближає модель до неперервної. У практичній реалізації це означає перехід від аналітичних методів розв’язування до чисельних методів (до покрокових обчислень за рекурентними виразами). І саме тут даються взнаки специфічні особливості комп’ю­терних обчислень – нагромадження похибок округлення різного походження. Їх вивчає окремий розділ обчислювальної математики – теорія дискретних математичних моделей, яка розробляє методи встановлення відповідності між обома типами моделей – неперерв­ними й дискретними. Визначення умов стійкості розрахункових
алгоритмів, тобто умов, за яких похибки обчислень не нагромаджуються, – одна з важливих задач дискретної математики.

Стосовно обговорюваного прикладу (і деяких наступних задач) ця теорія дає просту й надійну умову:

Δ t ≤ εh ²,

де Δ t – крок зміни по осі часу (аргументу);

ε – деяка постійна (іноді беруть ε = 1);

h – крок зміни іншої величини, яка залежить від часу (у нашому прикладі h відповідає кроку вздовж осі N).

З цієї умови випливає важливий висновок: якщо крок h малий (при великому кроці не буде досягнута очікувана точність), то крок Δ t вздовж осі часу має бути ще меншого порядку малості.

Таким чином, рис. 4.8 ніякого відношення до процесу не має. Справа в тому, що при збільшенні значень кроку приросту аргументу – інтервалу Δ t – перестає виконуватись умова достатньої малості цих інтервалів, в результаті чого стає нестійким сам обчислювальний процес, руйнується стійкість різницевого рівняння та розрахункового алгоритму. У таких ситуаціях результати моделювання, як правило, виявляються помилковими, а тому їм не слід довіряти.

Висновки

1. Розглянута модель була отримана з найпростішої моделі – моделі Мальтуса шляхом вдосконалення останньої, а саме врахуванням реальних обмежень на ресурси середовища. Це призвело до появи конкуренції між окремими особинами в популяції.

2. У відповідності з прийнятими припущеннями модель на
задовільному рівні відображає зміну чисельності особин у деяких природних популяціях. Зокрема, було встановлено існування рівноважного стану: за будь-яких відхилень від чисельності N _гр популяція самостійно повертається в цей стан. Таку рівновагу називають стійкою. Одночасно ми виявили фактори, від яких залежить значення N _гр – вмісту середовища.

3. За можливості математичну модель доцільно аналітично
перевіряти на наявність в ній рівноважних станів.

4. Обчислювальний експеримент дозволив виявити умови, за яких порушується стійкість розрахункового алгоритму. Такі ситуації потребують особливої уваги й аналізу, оскільки вони часто ведуть до помилкових висновків стосовно досліджуваної системи.

Що ж стосується наших карасів у ставку, то чи не настав час не тільки вести підрахунки чисельності, але й використовувати їх як харчовий ресурс?

Дата добавления: 2015-01-03