
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислювальний експеримент. Припустимо, що ми знов плануємо виловлювати максимально можливу кількість риби, тобто будемо вести вилов на рівні сmax
|
|
|
|
Припустимо, що ми знов плануємо виловлювати максимально можливу кількість риби, тобто будемо вести вилов на рівні сmax. Тоді значенню для s відповідатиме точка М перетину прямої с=s·N і параболи с=pN–q·N 2. Ця точка лежить у вершині параболи.
Вправа.
1. Доведіть, що цій точці відповідає s = p /2.
2. У деякій вільній комірці таблиці обчисліть значення параметра s. Чому той факт, що значення s помітно менше за сmax, не повинен викликати подиву?
3. 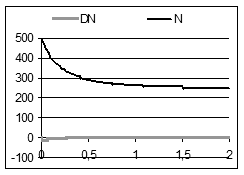 Створіть нову таблицю при N 0 = 500. Зверніть увагу: після деякого періоду усталення популяція виходить на рівноважний (стаціонарний) режим – її чисельність перестає змінюватись і залишається на рівні 250 (рис. 4.20). Чому саме 250?
Створіть нову таблицю при N 0 = 500. Зверніть увагу: після деякого періоду усталення популяція виходить на рівноважний (стаціонарний) режим – її чисельність перестає змінюватись і залишається на рівні 250 (рис. 4.20). Чому саме 250?
| A | В | C | D | E | |
| t | D N | N | Дано: | ||
| N 0 = | |||||
| 0,01 | -13 | p = | |||
| 0,02 | -12 | q = | 0,01 | ||
| 0,03 | -11 | s = | 2,5 | ||
| 0,04 | -10 | D t = | 0,01 | ||
| 0,05 | -9 | ||||
| 0,06 | -9 | ||||
| ... | ... | ... | ... |
Рис. 4.20.
4. У попередній версії результат був таким самим, але там було встановлено, що при с=сmax рівновага виявлялася нестійкою: при
випадковому зменшенні чисельності (N < N гр / 2 – ліва гілка параболи) популяція гинула. Дана версія позбавлена такої вади й у цьому легко переконатись.
5. Уменшіть N 0 до 100, залишаючи решту вхідних даних
незмінними. З отриманої таблиці ви дізнаєтесь, що популяція не тільки не гине, а, навпаки, чисельність її починає зростати, аж поки не стабілізується на значенні 200. До речі, як ви гадаєте, що відбуватиметься з популяцією при N 0 = 1? І взагалі, чи існує в даній моделі нижня границя для N 0? Перевірте свої припущення експериментально і дайте оцінку встановленому факту.
5.1 До позитивних якостей даної версії моделі слід віднести й те, що ця модель жорстко обумовлює межі можливих значень відносної квоти s у відповідності з (14). Будь-яка спроба виходу за ці межі призводить до одного з двох наслідків:
5.2 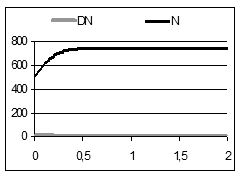 Значенням s <0 відповідає «від’ємний вилов», що рівноцінне додаванню риби у водоймище. Проте сказати про зазначену ситуацію словами прислів’я «носити дрова в ліс» – це ще сказати не все. Дійсно, якщо взяти s = -2,5, то одержуємо таблицю, з якої добре видно, що чисельність популяції не зростає необмежено (як це було б згідно прислів’я), а стабілізується на рівні 750 (рис. 4.21). Адже
Значенням s <0 відповідає «від’ємний вилов», що рівноцінне додаванню риби у водоймище. Проте сказати про зазначену ситуацію словами прислів’я «носити дрова в ліс» – це ще сказати не все. Дійсно, якщо взяти s = -2,5, то одержуємо таблицю, з якої добре видно, що чисельність популяції не зростає необмежено (як це було б згідно прислів’я), а стабілізується на рівні 750 (рис. 4.21). Адже
механізм обмеження, пов’язаного з конкуренцією, продовжує діяти!
| A | B | C | D | E | |
| t | D N | N | Дано: | ||
| N 0 = | |||||
| 0,01 | p = | ||||
| 0,02 | q = | 0,01 | |||
| 0,03 | s = | -2,5 | |||
| 0,04 | D t = | 0,01 | |||
| 0,05 | |||||
| 0,06 | |||||
| ... | ... | ... | ... |
Рис. 4.21
Вправа. Виконайте експерименти з N 0 = 200, 100, 10 при тому самому s = – 2,5. Зробіть висновки, порівнюючи граничні чисельності у кожному випадку.
5.3 При s > p пряма c = sN і парабола c = – qN 2 + pN (рис.4.18) не матимуть жодної точки перетину, окрім нецікавого випадку N = 0. Це означає, що рівноважних станів не існує: вилов перевищує реальні ресурси популяції, і вона гине.
Рис. 4.22 подає результат моделювання при N 0 = 500 і s = 7.
| A | B | C | D | 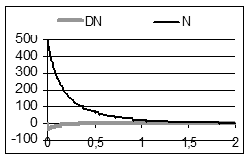 E E
| |
| t | D N | N | Дано: | ||
| N 0 = | |||||
| 0,01 | -35 | p = | |||
| 0,02 | -31 | q = | 0,01 | ||
| 0,03 | -28 | s = | |||
| 0,04 | -25 | D t = | 0,01 | ||
| 0,05 | -22 | ||||
| ... | ... | ... | ... |
Рис. 4.22.
Висновки
1. Модель вилову з негативним зворотним зв’язком здатна
забезпечити на довгий час оптимальний вилов – такий самий, як і при жорсткому плані з постійною абсолютною квотою. При цьому слід зазначити, що велика продуктивність тут неможлива. Однак при жорсткому плані внаслідок випадкових причин система може втратити стійкість і, отже, бути винищеною, а негативний зворотний зв’язок стабілізує її чисельність і відвертає від катастрофи.
2. Моделі, подібні до розглянутої, але помітно складніші, допомагають створювати стратегії ефективного використання відновлюваних природних ресурсів. Адже кінцевою метою управління ресурсами є не стільки плани їхнього використання, скільки правильно обрані стратегії планування.
3. Фахівці-екологи стверджують, що побудова сучасних математичних моделей в екології потребує впорядкування й класифікації численної наявної інформації стосовно екосистеми, веде до необхідності заздалегідь планувати збирання даних і дозволяє поєднати
сукупність фізичних, хімічних і біологічних відомостей та уявлень про окремі процеси, що відбуваються в екологічних системах.
Глава 5. Модель «хижак – жертва»
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 335; Нарушение авторских прав?; Мы поможем в написании вашей работы!