Обчислювальний експеримент. Підготуємо середовище для моделювання – електронну таблицю – за таким зразком: A B C D E F G t N1

Комп’ютерна модель

Підготуємо середовище для моделювання – електронну таблицю – за таким зразком:

	A	B	C	D	E	F	G
	t	N 1	N 2	Δ N 1	Δ N 2	Дано:
						k 1 =
						k 2 =
						а 1 =
						а 2 =
						N 01 =
						N 02 =
						Δ t =
…	...	...	...	...	...

Комірки другого рядка цієї таблиці (для моменту часу t = 0)
будуть мати такий уміст:

комірки	формули / числа
A2
B2	=$G$6
C2	=$G$7
D2	=B2*($G$2-$G$4*C2)*$G$8
E2	=-C2*($G$3-$G$5*B2)*$G$8

Заповнимо третій рядок, який потім скопіюємо у наступні n рядків, де n = t_{моделювавания} /Δ t:

комірки	формули
A3	=A2+$G$8
B3	=B2+D2
C3	=C2+E2
D3	=B3*($G$2-$G$4*C3)*$G$8
E3	=-C3*($G$3-$G$5*B3)*$G$8

Тепер можна починати

1. Введемо такі вхідні дані:

k ₁=5; k ₂=0,001; а =0,002; а ₂=10; t =0,01.D N ₀₁=15000; N ₀₂=2500;

2. Кількість рядків таблиці візьмемо п ≈ 400.

Результати моделювання показано на рис. 5.1.

	A	B	C	D	E	F	G
	t	N 1	N 2	D N 1	D N 2	Дано:
	0,00					k 1 =
	0,01			-38		k 2 =
	0,02			-77		a 1 =	0,002
	0,03			-117		a 2 =	0,001
	0,04			-158		N 01 =
	0,05			-198		N 02 =
	0,06			-238		D t =	0,01
...	...	...	...	...	...

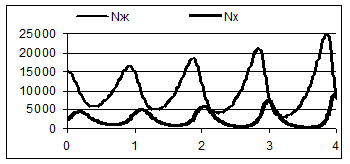
Рис. 5.1

3. З таблиці й графіків на рис. 5.1 видно, що зміни чисельності, як хижаків, так і жертв, є коливаннями з майже однаковими періодами (переконайтеся за таблицею) і зростаючими амплітудами.

Завдання

1. Чим, на вашу думку, обумовлене зростання амплітуд?

2. Як ви вважаєте, чому фази цих коливань не співпадають?

4. Дослідимо вплив параметрів моделі на перебіг процесу.
Загальноприйнятим тут є такий підхід: усі параметри моделі, крім одного, фіксуються, а незафіксованому параметру надають різних значень. Нехай для початку таким параметром буде N ₀₁.

4.1. Зменшимо N ₀₁, наприклад, від 15000 до 13000.

Чи змінився помітним чином період коливань?

4.2. Стосовно амплітуд коливань кількостей хижаків і жертв зазначимо, що тепер вони стали меншими.

Для того, щоб мати можливість проаналізувати результати впливу N ₀₁ на амплітуди цих коливань, будемо зменшувати N ₀₁ із певним кроком, наприклад, 2000, тобто надаватимемо N ₀₁ значень 15000, 13000, 11000, 9000, 7000, 5000. При цьому спостерігаємо, що амплітуди спочатку спадають (до N ₀₁ = 11000), а потім зростають (після N ₀₁ = 9000). Одразу виникає два питання:

а) при якому значенні N ₀₁ амплітуди коливань чисельності хижаків і жертв набувають мінімумів;

б) якими є ці мінімальні значення?

Узявши N ₀₁ = 10000, ми одразу одержуємо відповідь і, крім того, принципово важливий результат: модель Вольтерри – Лотки передбачає рівноважний стан (рис. 5.2).

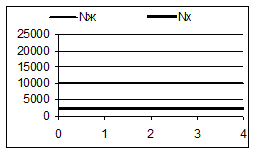
Рис. 5.2.

Тут слід зазначити, що нам просто пощастило. Якби значення параметра N ₀₁, що відповідає рівноважному стану, знаходилось не в точці 10000, то пошуки його шляхом обчислювальних експериментів могли б виявитись досить тривалими.

Після цього слід було б зафіксувати деяке значення параметру N ₀₁, а експериментувати з параметром N ₀₂.

Та виявляється, що в цьому немає ніякої необхідності: адже ми маємо вже певний досвід аналітичного пошуку рівноважних станів і можемо ним скористатись. Оскільки рівноважному стану відповідає Δ N ₁ = 0 і Δ N ₂ = 0, то з (2) одразу видно, що нулю повинні дорівнювати вирази в дужках: k ₁ – а ₁ N ₂= 0 і k ₂ – а ₂ N ₁= 0, звідки для будь-якого, в тому числі й початкового моменту t = 0, маємо

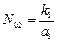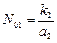и . (3)

Виконаємо перевірку: 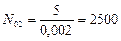і .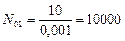

Отже, рівноважні стани повністю визначаються значеннями
параметрів k ₁, а ₁, k ₂ й а ₂ – коефіцієнти моделі.

При отриманні результату (3) передбачалося, що чисельності N ₁ і N ₂ не змінюються з часом (тому Δ N ₁ = 0 і Δ N ₂ = 0), і це – одне з
багатьох рішень – називають стаціонарним.

Звернемо тут увагу на наступну особливість. Модель Вольтéрри-Лотки нами була взята в готовому вигляді і виявилася досить складною. Коли ж моделі створювали ми самі, то йшли від найпростіших версій до все більш ускладнених, а отже й більш загальних. Такий метод побудови міркувань (від часткового до загального) назива­ється індуктивним. Часто, однак, для аналізу складних залежностей виявляється доцільним іти в протилежному напрямі – в бік спрощення моделі (системи рівнянь), тобто розглядати окремі спрощені
випадки. Відповідний метод міркувань (від загального до часткового) називають дедуктивним. До речі, в нашій ситуації це чи не єдиний шлях щось зрозуміти.

Коротко підсумуємо зроблене на даний момент.

1 На початку 30-х років ХХ ст. Віто Вольтéрра поєднав
математичне моделювання з популяційної екології, і в результаті з’явилося новий перетин наук – сучасна математична екологія.

2. Модель «хижак – жертва» не має аналітичних рішень, і єдиний вихід тут – це застосувати чисельне розв’язування, яке зручно проводити з використанням комп’ютера.

4. Залучення комп’ютера до розв’язування задач математичних екології привело на згаданий перетин ще одну природничу науку – інформатику та її основний засіб – комп’ютерне моделювання.

5. Наразі залишився не з’ясованим той факт, що періоди коливань чисельності хижаків і жертв, по-перше, однакові між собою і, по-друге, ці періоди не залежать від значень, що їх набувають N ₁ і N ₂ в процесі своєї зміни. Оскільки коливальні процеси є предметом
вивчення фізики, і ми вже скористалися деякими поняттями теорії коливань (амплітуда, період, фаза), фізика поки все ще не сказала свого вагомого слова.

5.1. Отже припустимо, що система «хижак – жертва» якимось чином (не важливо, яким саме) виявилася поблизу рівноваги. Нехай при цьому чисельності хижаків і жертв мало відрізняються від відповідних стаціонарних значень. Іншими словами, нехай

,

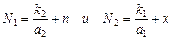де п та х малі в порівнянні з N ₁и N ₂.

Якщо підставити вирази (1) і знехтувати добутком пх унаслідок
його малості в порівнянні з іншими членами, то отримаємо

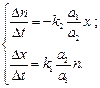(4)

Уведемо нову змінну 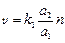. Після відповідної заміни система (1) набуває спрощеного вигляду:

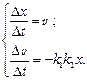(5)

5.2. Якби ми нічого не знали про модель Вольтéрри-Лотки, і
перед нами було б поставлене питання: «Що саме описує система рівнянь (5), де k ₁ і k ₂ – деякі постійні величини?», то рано чи пізно в цій системі ми б упізнали рівняння, що описують рух вантажу на пружині за умови, що х – мале зміщення вантажу від положення рівноваги, v – швидкість вантажу, а вираз k ₁∙ k ₂ має зміст відношення
жорсткості пружини до маси вантажу.

Отже, система (5) має такий самий розв’язок, як і задача про
малі коливання вантажу на пружині (пружинного маятника).

Збіг вигляду рівнянь, що описують коливання пружинного маятника і чисельності особин в системі «хижак – жертва» дозволяє стверджувати, що чисельності хижаків і жертв повинні змінюватися за гармонійним законом з періодом

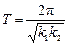. (6)

Якщо далі згадати, що коливання швидкості маятника випереджають за фазою коливання його координати на чверть періоду (на π /2 радіан), то слід зробити висновок, що коливання чисельності
хижаків також повинні випереджати коливання чисельності жертв на чверть періоду.

5.3. Таким чином, розв’язком системи рівнянь Вольтéрри-Лотки є коливання чисельності хижаків і жертв з періодом 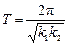, зсунуті одне відносно одного за фазою на π /2 радіан.

Відомо, що коли амплітуда таких коливань зростає, вони перестають описуватися законом косинуса або синуса, тобто перестають бути гармонійними, що видно з графіків на рис. 5.1, однак період
залишається практично незмінним.

Вправа

5.3.1. Чому період коливань не залежить від N ₁ і N ₂?

5.3.2. Обчисліть період Т згідно (6) і порівняйте отримане значення з тим, що дає таблиця з рис. 5.1, на якій зображено не менше трьох періодів. За результатами порівняння зробіть висновки.

5.3.3. Покажіть, що в пп. 5.1, 5.2, 5.3 був використаний метод аналогій (див. «Аналогове моделювання»).

5.4. Завершимо експериментальне дослідження моделі побудовою та аналізом графіків зміни чисельності обох популяцій залежно від часу згідно із спрощеною системою (5). Будемо мати на увазі, що система (1) автоматично переходить до спрощеного вигляду за умови, визначеної у п. 5.1, тобто коли початкові кількості особин кожного виду N ₀₁ і N ₀₂ мало відрізняються від своїх стаціонарних значень 10000 і 2500 відповідно. Для цього візьмемо для них такі, наприклад, значення: N ₀₁ = 10040 і N ₀₂ = 2520.

Результат, представлений на рис. 5.3, виявляється вкрай невиразним (перевірте!), а причина в тому, що на вертикальній осі ми спробували показати несумірні пари чисел 10000 і 40 та 2500 і 20.

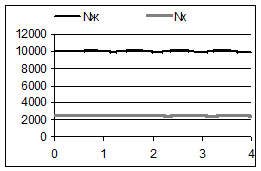
Рис. 5.3.

Чисельне розв’язування системи (2) привело до висновку, що з плином часу в популяціях і хижаків, і жертв відбуваються зсунуті за фазою періодичні коливання чисельності з наростаючою амплітудою (рис. 5.1).

У спрощеній системі (5) ці коливання набувають гармонічного характеру, але безпосередньо побачити цей факт досить складно:
результат на графіку, представленому на рис. 5.3 виявляється зовсім невиразним і непереконливим.

Наступний матеріал доцільно вивчати після розгляду теми
«Фазова площина» з Глави 7. Щоб отримати переконливу інформацію про досліджуваний процес, зобразимо його на фазовій площині в координатах N ₁, N ₂, що, як ми бачили, є аналогами зміщення x, і швидкості його зміни v, тобто виведемо на екран графіки залежності N ₂ = f (N ₁) – рис. 5.4.

З рис. 5.4(а) видно, наступне:

- процес дійсно є коливальним;

- амплітуда коливань постійно зростає.

Згущення траєкторії зображуючої точки біля координатних осей обумовлене тим, що величини N ₁ і N ₂ за своєю природою є додатними числами й не можуть набувати від’ємних значень, а тому вони «вимушені» групуватись у вузьких смугах біля осей.

Порівняно з рис. 5.1 ніяких принципово нових відомостей тут немає, а ось фазовий портрет процесу, показаний на рис. 5.4(б),
повністю усуває недоліки, виявлені при аналізі рис. 5.3.

В методі моделювання широко використовують два принципово різних підходи. При першому підході створюється математична
модель процесу і виконується аналітичне або чисельне розв’язування відповідних співвідношень, яке за можливості супроводжується графічними побудовами. Тут комп’ютер використовується як високоефективний обчислювальний засіб. Саме таким способом ми здійснили описане вище дослідження й усі попередні.

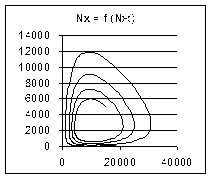
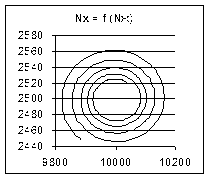
(а) N ₀₁ = 15000; N ₀₂ = 5000 (б) N ₀₁ = 10040; N ₀₂ = 2520

Рис. 5.4

Другий підхід – комп’ютерне імітаційне моделювання складної системи. Воно дозволяє отримати більш докладні уявлення про процеси. Зокрема, в моделі Вольтéрри-Лотки були б ураховані просторової неоднорідності). Але такий підхід потребує значно більш складних алгоритмів і великих витрат часу й пам’яті. Розв’язуючи такі задачі, дослідники активно використовують якісний аналіз, моделюють системи в спеціалізованих сучасних середовищах на спеціалізованих комп’ютерах, розробляють «правила гри» і розмірковують над тим, які з цих «правил» найбільш повно відповідають реальній системі. В цих моделях дуже часто характеристикам процесу присвоюють випадкові значення, і такі моделі називають імітаційними.
Докладніше про імітаційні моделі йтиметься далі в Розділах 11 та 12.

Вправа

5.4.1. Проаналізуйте рис. 5.4(б).

5.4.2. За рис. 5.1 з’ясуйте, чи утворюють послідовності максимумів функцій N ₁ = N ₁ (t) і N ₂ = N ₂(t) прогресії. Якщо так, то які саме: арифметичні чи геометричні?

5.4.3. Та все ж погодьтеся, не дуже віриться, що система «хижак – жертва» є таким собі генератором незатухаючих коливань!

Якщо ж з цим погодитися, то в такому разі в системі має бути позитивний зворотний зв’язок, необхідний для її переходу в режим генерації. Чим, на вашу думку, представлені елементи цього зв’язку?

5.4.4. Висловіть свої міркування стосовно джерела енергії, за рахунок якої можуть здійснюватися такі коливання (до того ж зі зростаючими амплітудами).

5.4.5. Як ви гадаєте, за яких умов, може статися затухання цих коливань?

5.4.6. Запропонуйте додаткові версії моделі, пов’язані з виловом жертв разом із хижаками (карасів зі щуками) одночасно, розробіть план таких досліджень та реалізуйте його.

Висновки

1. Модель Вольтéрри-Лотки передбачає процеси, що відбуваються тільки в просторово однорідних системах і нічого не говорить про можливий розвиток подій у випадках просторової неоднорідності. Тому вона, хоч і дає певною мірою адекватне рішення, але все-таки рішення це грубе. Модель дозволяє сформувати тільки «усереднене розуміння» того, як з плином часу змінюється кількість елементів системи.

2. Виявляється, що з не меншим успіхом моделлю Вольтéрри-Лотки можна скористатись і для з’ясування питань про кінетику
хімічних і ядерних реакцій (кінетика – це розвиток процесу у часі). Тут частинки реагентів безладно рухаються й унаслідок дифузії стикаються, вступають у реакції, в яких вони гинуть, продукуючи нові частинки тощо. Розмноженню риб відповідає, наприклад, ланцюгова ядерна реакція, їх загибелі – поглинання частинок (нейтронів) у реакторі. Для вирішення таких задач, як правило, складають рівняння, схожі на рівняння системи (1) і отримують попередні грубі й усереднені дані про досліджуваний процес. Схожі результати з’являються і при вивченні багатьох інших конкуруючих і взаємообумовлених процесів.

3. Таким чином, наше дослідження, яке починалося як пошук розв’язання задачі математичної екології, отримала несподіване продовження і підтримку з боку фізики. В кінцевому підсумку воно об’єднало чотири важливі галузі сучасного природознавства – популяційну екологію, математику, інформатику та фізику і виявилося проявом системного підходу при використанні комп’ютерної технології моделювання як інтегруючої основи сучасного природо­знавства.

Глава 6. Вікова модель одновидової
популяції

Дата добавления: 2015-01-03