Формалізована постановка задачі. Загальний опис моделі

I. Модель одновидової популяції за відсутності обмежень

Спрощено уявити собі одновидову популяцію, яка існує без зовнішніх обмежень, можна на такому ідеалізованому прикладі. Нехай у великому ставку розводять риб (наприклад карасів). Вони не заважають одне одному: їжі, світла й місця вистачає, хижаки відсутні й риб не виловлюють.

Метою дослідження поставимо пошук відповіді на питання:

Як змінюватиметься чисельність популяції з плином часу?

Нагадаємо, що моделі, в яких досліджується зміна в часі деяких характеристик (параметрів), називають динамічними.

Введемо такі позначення:

N ₀ – кількість особин на початку спостереження (у момент t = 0);

N – чисельність популяції в довільний момент часу t;

Δ N – приріст чисельності за досить малий проміжок часу Δ t (умову «достатньої малості» ми обговоримо дещо пізніше). Тоді
вираз 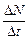матиме смисл середньої швидкості приросту чисельності за цей проміжок.

Цілком природно, що середня швидкість приросту популяції має залежати, в першу чергу, від чинників, що характеризують здатність особин до відтворення й одночасно – їхню здатність до виживання. Введемо відповідні параметри:

а – коефіцієнт народжуваності;

b – коефіцієнт смертності.

Цим коефіцієнтам надамо такого смислу: якщо чисельність
популяції в деякий момент часу складає N особин, то за проміжок часу Δ t від них народжуються aN особин і одночасно bN особин
гинуть. У такому разі ефективний приріст чисельності D N = (a – b)· N, причому в разі зростання чисельності а > b, а при її зменшенні а < b.

Позначимо далі k = а – b. У математичній екології параметр k є кількісною характеристикою здатності популяції до чисельного зростання і називається коефіцієнтом приросту.

Спостереження показують, що в природних умовах

1) параметри a і b, а отже і k, змінюються з часом (з віком особин);

2) у багатьох біологічних видів моменти появи потомства від окремої особини мають зазвичай майже періодичний характер, але у великій сукупності різних особин ці періоди можуть перекриватися, так що фактично потомство з’являється постійно й неперервно.

З метою спрощення приймемо ряд припущень.

Припущення 1. Вважатимемо, що за незмінних зовнішніх умов

– коефіцієнт народжуваності k є постійною в часі величиною;

– народження й загибель особин відбуваються неперервно;

– тривалість життя кожної особини значно менша за час «спостереження» (час моделювання).

Нехай за деякий і -й досить малий інтервал часу Δ t (і – порядковий номер інтервалу) чисельність популяції зростає на D N. Тоді на початок наступного такого ж інтервалу з номером і +1 чисельність складатиме N_{і+ 1}. Зрозуміло, що більша кількість особин за такий
самий проміжок часу Δ t даватиме більший приріст D N, тому середня швидкість приросту D N /Δ t повинна зростати. За незмінних зовнішніх умов швидкість приросту залежить від чисельності популяції в даний момент. Проте вигляд цієї залежності нам невідомий і може бути різним. Маючи на меті створення простої моделі, приймемо

Припущення 2. Нехай залежність середньої швидкості приросту від чисельності популяції в даний момент є простою – прямою пропорційною:

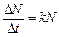. (1)

Якщо переписати (1) у вигляді

Δ N = k · N ·Δ t, (2)

то можна сказати, що за будь-який достатньо малий проміжок часу Δ t приріст Δ N чисельності пропорційний як кількості особин на
початку проміжку Δ t, так і тривалості цього проміжку.

Вираз (2) є записаним, як то кажуть, у формі кінцевих різниць.

Характерною властивістю рівнянь такого виду є те, що вони справедливі лише для малих приростів аргументів, підстановка в них довільних значень аргументів є некоректною.

Згідно (1) або (2)

,

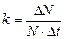тобто чисельно параметр k дорівнює відносному приросту Δ N / N за одиницю часу.

Рівняння (1) уперше було запропоноване в 1798 р. англійським вченим Томасом Мальтусом і в математичній екології дістало назву «Модель Мальтуса».

Це рівняння містить невідому величину N і швидкість її зміни D N /Δ t.

Вище вже відзначалося, що засобами елементарної математики рівняння такого типу не розв’язуються, тому скористаємося чисельним методом – покроковим розв’язуванням:

1. У початковий момент часу (t = 0) покладемо N=N ₀ і Δ N = 0.

2. Наступний момент візьмемо в кінці першого проміжку Δ t і згідно (2) обчислимо Δ N – зміну кількості особин за цей проміжок.

3. Знайдемо нову кількість особин N_і, додаючи до попереднього значення N_{і- 1} щойно обчислену зміну

N_і = N_{і- 1} + Δ N. (3)

4. Підстановкою (2) в (3) отримаємо

N_і = N_{і- 1} + k·N_{і- 1}·Δ t. (4)

5. Повторюючи пункти 2 і 3 для наступних проміжків часу
t_і = t_{і – 1} +Δ t, знаходитимемо відповідні нові значення N.

Рівняння (2) і (3) або (4) є математичною моделлю динаміки
одновидової популяції за відсутності обмежень. Вони дозволяють знайти чисельність популяції в інтервалі Δ t з номером і, якщо відома чисельність на попередньому інтервалі з номером (і -1). Рівняння (4), таким чином, є рекурентним.

Як і раніше, швидкість приросту D N /Δ t можна оцінювати за значеннями приростів D N, оскільки всі проміжки Δ t однакові.

Зауваження 1. Проміжки часу Δ t, які фігурують у даній математичній моделі, як і самий час t, доцільно представляти в умовних одиницях. Залежно від біологічного виду це можуть бути хвилини, години, роки тощо Важливо лише, щоб ці проміжки Δ t були набагато меншими за час моделювання, і щоб протягом такого проміжку приріст чисельності Δ N становив малу частку від загальної кількості особин N на даний момент. Саме в такий спосіб і буде задовольнятися умова «достатньої малості» проміжку часу. Що може відбуватися з моделлю при порушенні цієї умови, ми обговоримо пізніше.

Оскільки задача сформульована і створена її математична
модель, запишемо

Дата добавления: 2015-01-03