Остаточний алгоритм. Комп’ютерна модель

1. Підготувати таблицю за зразком:

	A	B	C	D	E	F	G	H	І	J	K
	t	vx	vy	v	a	ax	ay	x	y	Дано:
										x 0 =
										y 0 =
										v 0 =
										a 0 =
										Δ t =
										g =
										R =
										Q =
...	...	...	...	...	...	...	...	...	...

2. Увести вхідні дані для початкового моменту часу t = 0, тобто заповнити стовпець J («Дано:») і перший рядок таблиці іменами змінних, а стовпець К – їхніми числовими значеннями згідно умови:

- x ₀, y ₀ – початкові координати;

- v ₀ – початкова швидкість;

- a₀ – початковий кут нахилу вектора v ₀ до горизонту;

- g = 9,81 – прискорення сили тяжіння;

- R – фактор дії сили опору;

- Q – фактор дії підіймальної сили.

3. Заповнити другий рядок (для t = 0):

- t = 0;

- v_x = v ₀cos a ₀; v_y = v ₀sіn a ₀; v = v ₀;

- a = a₀;

- a_x = –v ²(R cos a + Q sіn a); a_y = – g + v ²(Q cos a – R sіn a)

- x = x ₀; y = y ₀.

Комірки таблиці матимуть такий уміст:

комірки	формули / числа
A2
B2	= K4*COS(K5*ПИ()/180)
C2	= K4*SІN(K5*ПИ()/180)
D2	= K4
E2	= K5
F2	= -(D2^2)*(K8*COS(E2*ПИ()/180) + K9*SІN(E2*ПИ()/180))
G2	=- K7 + D2^2*(K9*COS(E2*ПИ()/180)-K8*SІN(E2*ПИ()/180))
H2	= K2
І2	= K3

Примітки.

а) при обчисленні прямих та обернених тригонометричних функцій (для комірок B2, C2, F2 та G2) електронні таблиці, як і переважна більшість інших програмних засобів, працюють з радіанною
мірою кутів, проте для школярів більш звичним та наочним є використання градусної міри. У зв’язку з цим скористаємося формулою переходу від градусної міри до радіанної: φ(рад) = a(град)·π/180.

б) комірки B2 та C2 містять значення v _{0 х} , v _{0 у} – проекцій вектора початкової швидкості v ₀ на вісі координат.

4. Заповнити третій рядок (для кінця першого проміжку D t, тобто для моменту часу t _і= t_{і– 1} + D t, де і = 1):

- v_іx = v _{(і– 1) x} + a_іx D t; v_іy = v _{(і– 1) y} + a_іy D t

-

-

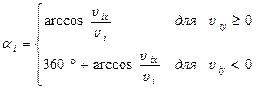
- a_іx = -v_і ²(R cos a _і + Q sіn a _і);

- a_іy = – g + v_і ²(Q cos a _і – R sіn a _і)

- x_і = x_{і– 1} + v_іx D t; y_і = y_{і– 1} + v_іy D t

Відповідно у таблиці

	комірка	формули / числа
A3	= A2 + K$6
B3	= B2 + F2*K$6
C3	= C2 + G2*K$6
D3	= (B3^2 + C3^2)^0,5
E3	= ЕСЛИ(C3> = 0;ACOS(B3/D3)*180/ПИ(); 360-ACOS(B3/D3)*180/ПИ())
F3	= -(D3^2)*(K$8*COS(E3*ПИ()/180) + K$9*SІN(E3*ПИ()/180))
G3	= -K$7 + D3^2*(K$9*COS(E3*ПИ()/180)-K$8*SІN(E3*ПИ()/180))
H3	= H2 + B3*K$6
І3	= І2 + C3*K$6

5. Копіювати третій рядок у n наступних рядків (n = t _{польоту} /D t).

ІІ. Рух тіла під дією сили тяжіння (тестування моделі)

У відповідності до загального плану роботи розглянемо приклади руху тіл під дією однієї лише сили тяжіння F _т, знайомі нам зі
шкільного курсу механіки. Оскільки в цих випадках дією середовища на тіло звичайно нехтують, то й ми покладемо Q = 0 і R = 0,тобто виключимо з розгляду обидва фактори аеродинамічної сили.

1. Спочатку дослідимо рух тіла, кинутого вертикально.

Нехай тіло починає рухатись над плоскою горизонтальною поверхнею з початковою швидкістю v ₀ = 10 м/c з точки, що має координати х ₀= 0, y ₀ = 20 м. Рух тіла відбувається

1.1. вертикально вгору (a₀ = 90°);

1.2. вертикально вниз (a₀ = 270° або a₀ = - 90°);

1.3. без початкової швидкості (v ₀ = 0).

Вправа. По черзі виведіть на екран і розгляньте три таблиці за пп. 1.1 – 1.3.

У кожній з таблиць можна побачити, що час підйому та повний час польоту повністю відповідають розрахованим заздалегідь за
формулами

v_у = v _{0 у} – gt,

y = y ₀ + v _{0 у} t – gt ² / 2.

Перша з цих формул дає час підйому при v_у = 0 (коли спливає час підйому, вертикальна складова швидкості зменшується до нуля, тобто у верхній точці траєкторії тіло завмирає).

Наступна формула дає повний час польоту при у = 0. Дійсно,
коли закінчується повний час польоту, тіло виявляється на поверхні землі. До речі, наша модель цих формул не передбачає.

У випадках 1.2 і 1.3 кут a автоматично перетворюється на a = 270°, а у випадку v ₀ = 0, це має місце за будь-яких значень a₀ (!).

Той факт, що у всіх стовпцях, де розташовані проекції змінних на вісь Ох, з’являються нулі, повністю узгоджується з умовою, що a₀ – прямий кут і, отже, v _{0 x} = v ₀ cosa₀ = 0. Це зрозуміло й з фізичних міркувань, але зараз ми маємо нагоду впевнитися в тому, що даний результат одержано на основі прийнятої моделі.

2. Продовжимо тестування. Розглянемо рух тіла, кинутого під кутом до горизонту.

2.1. Почнемо з прикладу, коли тіло кидають горизонтально (a₀ = 0). Початкові значення координат х ₀, у ₀ і швидкості v ₀ залишимо попередніми.

Вправа.

1. Доведіть, що за відсутності в алгоритмі помилок нулі мають залишитись тільки у стовпці для значень a_x.

2. За таблицею встановіть, що будь-яким однаковим послідовним проміжкам часу відповідають однакові прирости D х,а прирости для D y послідовно зростають (спадають) на одну й ту саму величину. Отже залежність y від х не є лінійною. згадану властивість має тільки єдина – квадратична функція.

3. Беручи аргументами значення змінних із стовпця x, побудуйте траєкторію тіла – графік залежності y = y (x), як показано на рис. 9.2.

	A	B	C	D	E	F	G	H	І	J	K
	t	vx	vy	v	a	ax	ay	x	y	Дано:
	0,0	10,00	0,00	10,00		0,00	-9,81	0,00	20,00	x 0 =
	0,10		-1				-10	1,00	19,90	y 0 =
	0,20		-2				-10	2,00	19,71	v 0 =
	0,30		-3				-10	3,00	19,41	a0 =
	0,40		-4				-10	4,00	19,02	Δ t =	0,1
	0,50		-5				-10	5,00	18,53	g =	9,81
	0,60		-6				-10	6,00	17,94	R =
	0,70		-7				-10	7,00	17,25	Q =
...	...	...	...	...	...	...	...	...	...

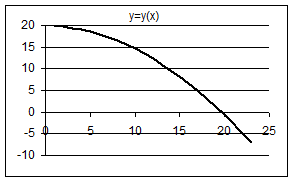
Рис. 9.2

Перевіримо модель на прикладі стандартної задачі.

Задача. Літак летить горизонтально на висоті 100 м зі швидкістю 100 м/с. Від літака відокремлюється вантаж, який починає падати вниз. Нехтуючи опором повітря, знайти:

- скільки часу вантаж перебуватиме в польоті?

- на якій відстані від місця призначення (вздовж вісі Ox) треба звільнити вантаж, щоб він потрапив у це місце?

- з якою швидкістю вантаж торкнеться землі?

Змінимо згідно умови вміст комірок у попередній таблиці:

комірки	числа	коментарі
К3		початкова висота у 0
К4		початкова швидкість v 0

Порівнюючи відповіді, одержані за допомогою фізичних формул, з даними, одержаними за допомогою моделі (таблиці та графіка y = y (x), можна переконатись, що вони добре узгоджуються.

2.2. Поширимо тестування на довільні кути.

Нехай, для визначеності, з точки, що має координати x ₀ = 0, y ₀ = 0 (початкові координати), з пружинного пістолета вистрілюють кульку під кутом a₀ = 60° з початковою швидкістю v ₀ = 5 м/с (рис. 9.3).

З отриманої таблиці маємо можливість побачити, що

	A	B	C	D	E	F	G	H	I	J	K
	t	vx	vy	v	a	ax	ay	x	y	Дано:
	0,00	2,5	4,330	5,000			-9,81	0,00	0,00	x 0 =
	0,05	2,5	3,840	4,582			-9,81	0,13	0,19	y 0 =
	0,10	2,5	3,349	4,179			-9,81	0,25	0,36	v 0 =
	0,15	2,5	2,859	3,798			-9,81	0,38	0,50	a 0 =
	0,20	2,5	2,368	3,444			-9,81	0,50	0,62	D t=	0,05
	0,25	2,5	1,878	3,127			-9,81	0,63	0,71	g=	9,81
	0,30	2,5	1,387	2,859			-9,81	0,75	0,78	R=
	0,35	2,5	0,897	2,656			-9,81	0,88	0,83	Q=
...	...	...	...	...	...	...	...	...	...

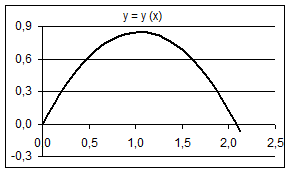
Рис. 9.3.

– часи підйому і падіння, а також повний час польоту співпадають з розрахованими теоретично (за формулами);

– миттєві значення змінних а_y, v_y, v, y та a у межах усталеної точності є симетричними відносно моменту часу, що відповідає максимальній висоті підйому тіла.

Далі звернемося до задачі нестандартної.

Задача. Згідно з легендою відомий своєю влучністю Робін Гуд, маючи на меті передати листа в’язневі Ноттінгемського замку,
загорнув у цей лист камінь і кинув його так, що камінь перелетів огорожу і точно потрапив у вікно в’язниці. Вважаючи, що камінь був кинутий з відстані d від огорожі висотою h і що вікно в’язниці знаходилося на відстані D від місця кидання (вздовж горизонталі) і було на висоті H, знайти, під яким кутом і з якою мінімальною початковою швидкістю був кинутий камінь? У момент кидання камінь знаходився на висоті Z. Опором повітря знехтувати.

Виконаємо теоретичний розрахунок за такими даними:

х ₀ = 0, y ₀ = Z = 2 м;

х ₁ = d = 8 м; y ₁ = h = 6,8 м;

х ₂ = D = 13 м; y ₂ = H = 5,5 м.

Спростимо розв’язування, поклавши Z = 0.

Примітка. Оскільки зазначені три точки знаходяться на одній траєкторії (параболі), то, написавши двічірівняння траєкторії для x ₁ = d, y ₁ = h та для x ₂ = D, y ₂ = H, після перетворень можна одержати систему двох рівнянь з двома невідомими v ₀ та a₀. Ця система являтиме собою математичну (не комп’ютерну) модель руху тіла, кинутого під кутом до горизонту.

Після математичного розв’язання задачі введемо до комп’ютер­ної моделі (таблиці) одержані відповіді як значення v ₀ та a₀ і перевіримо результати моделювання, якими тепер стають значення змінних х та y. При цьому бажано зменшити інтервал Δ t до 0,01, збільшивши відповідно кількість рядків таблиці додатковим копіюванням останнього рядка формул.

Дійсно, в отриманій на екрані таблиці ми виявляємо дві пари
координат, що відповідають заданим в умові точкам: Х ₁, Y ₁ та Х ₂, Y ₂.

Завдання. Дайте фізичне тлумачення отриманому результату, виконайте відповідний рисунок.

Дата добавления: 2015-01-03