Аналіз умови й обговорення плану роботи

Формалізація задачі та побудова моделі

Уведемо позначення:

M – маса модуля без урахування маси пального (за умовою п. 5 величина стала).

m = m_t – змінна маса пального. У початковий момент m = m ₀.

r – витрата пального, тобто маса пального, що спалюється в
камерах згоряння двигунів м’якої посадки за проміжок часу від
моменту t до t + D t, тобто за проміжок часу D t. Оскільки припускається, що витрату можна регулювати в ході зниження, то r є невідомою і шуканою функцією часу: r = r (t).

Зазначене вище обмеження на витрату пального (п. 3 технічних умов) можна записати у вигляді нерівності 0 ≤ r (t) ≤ r_max.

v = v_t – миттєва швидкість модуля під час опускання. Початкова умова «зависання» виражається рівністю v ₀ = 0. Умова м’якої посадки – одночасне виконання нерівностей 0 ≥ v ≥ –1 і h ≤ 0.

u – швидкість витікання реактивного струменя; величина стала згідно п. 4 технічних умов.

h_t – миттєве значення висоти над поверхнею Місяця, причому h = h ₀ при t = 0.

Решту позначень будемо вводити в міру необхідності.

1. Рух, що його ми збираємось дослідити, з фізичної точки зору являє собою неперервний у часі й просторі процес. Дійсно, тут неперервно відбуваються зміни значень всіх динамічних і кінематичних характеристик рухомого об’єкта: маси, рівнодійної всіх діючих сил, прискорення, швидкості, імпульсу, координати тощо. Згадаємо, що математичні моделі, створені для опрацювання за допомогою комп’ютера (комп’ютерні математичні моделі), повинні бути дискретними, оскільки сам комп’ютер є дискретним пристроєм, тобто виконує операції за окремими кроками. Тому при комп’ютерному опрацюванні неперервних аналітичних моделей завжди існує потреба в уведенні до моделі елементів дискретизації.

Ця потреба реалізується на основі чисельних методів шляхом
переходу від неперервної математичної моделі до рівнянь, записаних у формі скінчених різниць. З попереднього досвіду ви вже знаєте, що для дискретизації неперервного в часі процесу, яким, зокрема, є механічний рух, весь час руху розбивають на окремі достатньо малі інтервали D t. При цьому вважають, що протягом такого інтервалу характеристики руху (значення відповідних змінних) залишаються постійними, а їхні зміни відбуваються миттєво (стрибкоподібно) в моменти часу, що відповідають кінцю або середині кожного такого інтервалу. Ці моменти, а також тривалість проміжків D t обирає дослідник. При послідовному зменшенні D t результати, одержані на дискретній моделі, наближаються до результатів, що їх дає аналітичне розв’язування за неперервною моделлю, якщо воно існує і відоме.

З метою спрощення подальших міркувань приймемо такі припущення.

Припущення 1. Протягом проміжку часу D t аж до його останньої миті повна маса модуля m + M і його швидкість v залишаються незмінними. В останній момент миттєво спалюється пальне масою r і це приводить до одночасної зміни значень згаданих характеристик. Ці нові значення стають початковими для наступного інтервалу D t, адже, як уже багаторазово зазначалося, кінець даного інтервалу є
початком наступного.

Розглянемо окремі елементарні моделі, при об’єднанні яких буде побудована загальна математична модель м’якої посадки модуля. В основу побудови покладемо рис. 10.1.

Рис. 10.1

1. Модель вигоряння пального.

m_t = m_{t– D t} – r_{t– D t} , (1)

де 0 ≤ r_t ≤ r_max;

m_t – маса пального в момент t;

m_{t– D t} – маса пального в момент (t- D t), тобто на попередньому проміжку D t;

r_{t– D t} – витрата пального на проміжку, що був на D t раніше за момент часу t, або маса пального, що згоріло за попередній проміжок часу D t.

2. Модель гравітаційного притягання Місяця.

, (2)

де g= 1,62 м/с² – прискорення сили тяжіння поблизу поверхні Місяця.

3. Модель реактивної сили тяги.

Реактивна сила тяги F_реакт, що діє на модуль, дорівнює швидкості зміни імпульсу модуля:

.

Згідно закону збереження імпульсу для замкнутої системи
«модуль – реактивна струмина» зміна імпульсу модуля за абсолютною величиною дорівнює зміні імпульсу струмини:

,

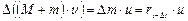де ∆ т = m_{t– D t} – m_t = r_{t– D t} – маса струмини, що витікає за проміжок часу D t згідно (1).

Таким чином,

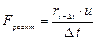. (3)

4. Модель руху модуля.

Внаслідок відсутності на Місяці атмосфери силу опору рухові з боку середовища можна не включати до розгляду. Тому на активній ділянці спуску, коли працюють тільки двигуни м’якої посадки, на модуль діють тільки дві сили: сила гравітаційного притягання Місяця F_тяж і протилежно напрямлена реактивна сила тяги F_реакт. За другим законом Ньютона рівнодійна цих сил надає модулеві прискорення:

,

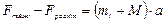де а = а_t – прискорення апарату, яке змінюється з часом.

Підставляючи (2) і (3) в останній вираз, будемо мати:

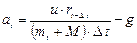. (4)

Оскільки розглядається рух тіла змінної маси, то прискорення виявляється складною функцією часу.

Припущення 2. Приймемо наближено, що прискорення а (t)
залишається сталим на кожному малому інтервалі D t, тобто рух
апарату на кожному часовому інтервалі є рівноприскореним. Тоді миттєва швидкість модуля v_t наприкінці інтервалу може бути визначена з виразу

v_t = v_{t– D t} + a_t∙ D t. (5)

Висота h_t над поверхнею Місяця може бути задана виразом

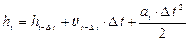. (6)

Система рівнянь (1), (4), (5), (6) являє собою математичну
модель м’якої посадки на Місяць.

Суттєвого спрощення подальшої роботи можна досягти, прийнявши тривалість інтервалу D t рівною одиниці часу: D t = 1. Проте
платнею за таке спрощення стане погіршення точності результатів. На якісному рівні, однак, модель залишатиметься задовільною. З урахуванням сказаного запишемо систему:

(7)

Цю систему рівнянь відносно m_t, a_t, v_t, h_t будемо розв’язувати методом послідовних підстановок. Суть методу полягає в такому. Нехай обрано деяке припустиме управління апаратом, тобто є заданою послідовність значень r ₀, r ₁, …, r_t, така, що r ₀ + r ₁ + … + r_t ≤ m ₀. При t = 0 нам уже відомі значення m ₀, a ₀, v ₀, h ₀ і, отже, можна обчислити значення правих частин у рівняннях системи (7), тобто знайти m ₁, a ₁, v ₁, h ₁. У свою чергу, їх можна використати для обчислення значень m ₂, a ₂, v ₂, h ₂ і т.д.

Послідовність значень r стане відомою лише після того, як ми відшукаємо її під час роботи з моделлю, тобто під час «гри».

Процес обчислень має тривати до моменту виконання умови h_{t +1} ≤ 0, тобто досягнення поверхні. Якщо при цьому одночасно виявиться, що –1 ≤ v_{t +1} ≤ 0, то посадку будемо вважати м’якою.

Вправа

1. Поясніть, чому досягнення поверхні ми описуємо умовою h ≤ 0, а не більш жорсткою h = 0?

2. Поясніть необхідність подвійної нерівності в умові для кінцевої швидкості м’якої посадки.

Система рівнянь (7) є рекурентною. Алгоритм її розв’язування передбачає виконання однотипних обчислень при t = 0, t = 1, …. Зрозуміло, що з подібною одноманітною роботою комп’ютер вправляється краще за людину. При математичному моделюванні реальних процесів і явищ на сучасних ЕОМ доводиться розв’язувати системи численних рекурентних рівнянь з багатьма невідомими.

Дата добавления: 2015-01-03