Післямова

При задовільній простоті та наочності електронних таблиць слід розуміти, що вони є придатним середовищем для моделювання тільки на початковому етапі. Так, вже при спробах розв’язання задач, що передбачають організацію циклів з великою кількістю повторень, звичайне копіювання формул у відповідні стовпці з метою нових розрахунків та утримання даних для подальшої побудови графіків (тобто організація великих масивів даних) викликає значні утруднення, позбавляючи користувача змоги простежити динаміку зміни значень будь-якої величини переглядом відповідного стовпця.
Нарешті, електронні таблиці стають зовсім непридатними для задач, що вимагають засобів візуального спостереження динаміки процесу, тобто візуалізації поточних станів об’єкту. Такі задачі традиційно розв’язують з використанням середовищ, створених на основі мов програмування високого рівня. Отже одним із критеріїв необхідності зміни середовища моделювання є ситуація, коли сама таблиця перестає використовуватись для аналізу даних, залишаючи користувачеві можливість лише графічного подання залежностей між даними.

Наприклад, у задачі на побудову траєкторії руху планети навколо Сонця повна таблиця містить близько 400 рядків, і це дійсно утруднює аналіз даних. Розгляд усіх дев’яти планет разом із Сонцем вимагатиме вже близько 90500 рядків, що об’єктивно зумовлює
потребу в іншому середовищі.

Ось чому повний курс основ комп’ютерного моделювання після початкового етапу включає ще дві важливі частини: вивчення методів ефективного використання ресурсів комп’ютера для розв’язання задач моделювання та вивчення об’єктно-орієнтованого підходу до моделювання динамічних систем, де засоби й методи спрямовуються на опанування все більш досконалих прийомів роботи, які можна здійснити в середовищі мови програмування. І хоч перехід від електронних таблиць до мови програмування позбавляє зручності миттєвої зміни параметрів моделі та наочності процесу розрахунків, проте надає ряд нових можливостей: 1) групування подібних між собою змінних у масиви; 2) зняття обмежень на кількість ітерацій та послаблення обмежень на кількість змінних; 3) графічна інтерпретація
динаміки моделі в процесі розрахунків (а не після їх закінчення, як в електронних таблицях).

Насправді існує можливість, залишаючись у середовищі електронних таблиць, використати вбудовану мову програмування, наприклад, Vіsual Basіc – внутрішню мову електронних таблиць Excel.
Такий крок дозволяє об’єднати переваги електронних таблиць та мов програмування високого рівня, проте орієнтація на мову програмування лише однієї фірми неминуче ставить користувача у залежність від стратегії розвитку мови, а ця стратегія обирається фірмами
переважно з комерційних міркувань. До того ж значна швидкість еволюції такої мови, відсутність інваріантного (незмінного) ядра та переобтяженість додатковими можливостями підвищують вимоги до техніки і утруднюють вивчення такої мови в школі.

Тому в якості наступного середовища для моделювання ми
використовуємо процедурну мову високого рівня. Однією з найпоширеніших мов високого рівня, що користується великою популярністю в системі освіти США, Франції, Німеччини та інших країн, є мова С. Доступність некомерційних та ліцензованих для закладів освіти операційних систем і компіляторів цієї мови дозволяє використовувати їх майже на всіх типах техніки, встановлених у наших школах.

Перехід до моделювання в середовищі мови програмування так само, як і перехід від паперових розрахунків до електронних таблиць, є еволюційним кроком, спрямованим на підвищення ефективності процесу розв’язання задач моделювання.

Усі згадані середовища відображають не стільки саму модель, скільки алгоритм роботи з нею, формалізований засобами процедурної методології.

Свого часу автори першої об’єктно-орієнтованої мови програмування Sіmula-67 наголошували на тому, що об’єктно-орієнтоване
середовище є природним середовищем для розв’язання задач моделювання (sіmulatіon). Об’єктно-орієнтований підхід (ООП) вносить якісні зміни у самий процес моделювання, надаючи потужні можливості щодо підвищення рівня абстракції даних. Сьогодні такі можливості серед інших мов має мова С++, яка легко пристосовується для використання в спеціальних областях шляхом створення на її базі складених понять та конструкцій, що слугують будівельними блоками при програмуванні. Так наявність у ній типу «арифметичний
вектор» та визначених операцій над ним спрощує запис програми, наближуючи його до алгоритмічного. До того ж об’єктно-орієнтоване середовище дозволяє від групування зазначених вище параметрів за ознакою спільності фізичного змісту перейти до групування за ознакою «бути планетою». В такому разі ми розглядатимемо Сонячну систему як набір планет (вважаючи Сонце однією з них), а не як сукупність прискорень, швидкостей, координат тощо.

Групування даних за ознакою «бути планетою» не є прерогативою ООП, воно можливе і в процедурній методології. Але принциповою перевагою ООП є те, що об’єкти не лише зберігають свої дані, а й змінюють їх, обмінюються інформацією, взаємодіють тощо. В
даному випадку взаємодія об’єктів типу «планета» є інформаційною моделлю фізичної взаємодії. Об’єктно-орієнтоване середовище
моделювання у найбільшій мірі відображує підходи сучасного комп’ютерного моделювання та є ефективним інструментом не лише при навчанні, а й у професійній діяльності.

Нижче на рисунку зображено модель Сонячної системи, створену засобами мови С++ за технологією ООП.

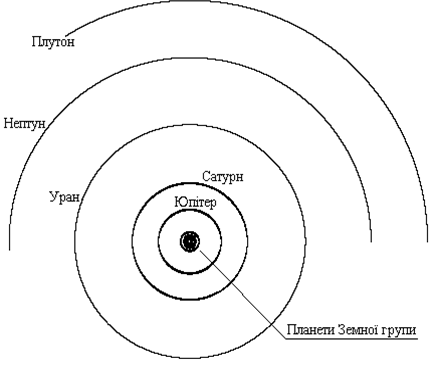
Стан Сонячної системи на момент
завершення Ураном повного оберту

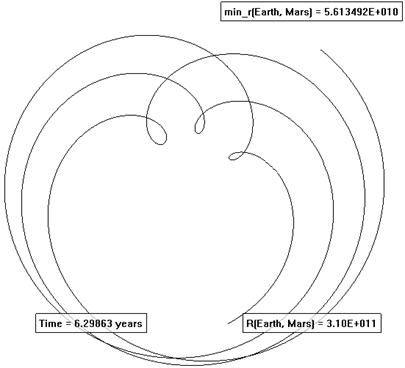
На наступному рисунку подані результати моделювання руху Марсу з точки зору земного спостерігача (в системі відліку, пов’язаній із Землею). Розрахунок показує, що за 6 років відбулося три протистояння, і останнє з них виявилося великим – обчислена мінімальна відстань склала 56 млн. 135 тис. км.

1.	Абстракція – одна з форм пізнання, що полягає в мисленому відволіканні від ряду властивостей предметів і відношень між ними й виокремленні деякої властивості або відношення.
2.	Автоматизована система управління (керування) (АСУ) – автоматизована система, заснована на комплексному використанні економіко-математичних методів і технічних засобів обробки інформації для розв’язування задач керування виробничо-господарською діяльністю різних ланок народного господарства
3.	Адекватність моделі – правильне відтворення моделлю властивостей, зв’язків і відношень оригінала.
4.	Адреса даних – адреса поля пам’яті, в якому розміщені дані.
5.	Алгоритм – набір інструкцій для виконавця, що дає можливість розв’язати конкретну задачу або клас задач.
6.	Аналогія – подібність в деяких якостях і відношеннях між різними за природою об’єктами. Важливою сферою застосування аналогії є розвинута в моделюванні теорія подібності.
7.	Аналогове моделювання – математичне моделювання, засноване на аналогії (схожості за деякими ознаками) процесів та явищ, що мають різну фізичну природу, але описуються однаковими за виглядом рівняннями, логічними схемами тощо.
8.	Атрибут – властивість (ознака), що містить одну з характеристик даної величини.
9.	Буфер обміну – спеціальна область оперативної пам’яті, яка резервується операційною системою для збереження даних.
10.	Величина – одиниця даних, що представлена своїм ім’ям і своїм значенням.
11.	Випадкова (статистична) вибірка – набір значень деякої характеристики певного процесу, отриманий із множини можливих значень досліджуваної характеристики.
12.	Випадкова змінна – змінна, що набуває довільного значення з певної області значень.
13.	Випадкове число – число, частота повторення якого у вибраній послідовності визначається технікою використання випадкової вибірки з множини допустимих значень.
14.	Вихідні дані – результат виконання програми.
15.	Вхідні дані – дані, які вводяться до програми для обробки або зберігання.
16.	Групування (статистичне) – розчленування елементів статистичної сукупності на окремі групи за певною ознакою.Завдяки групуванню матеріал спостережень набуває впорядкованого (систематизованого) вигляду.
17.	Дані – інформація, подана у вигляді, придатному для обробки (опрацювання) автоматичними засобами за можливої участі людини.
18.	Детермінована модель – модель, що відповідає причинно обумовленому об’єкту (явищу, процесу).
19.	Динамічна модель – модель, в якій досліджується зміна в часі деякої величини.
20.	Динамічні характеристики – характеристики об’єкту, що залежать від часу.
21.	Дискретизація – 1) вимірювання значень неперервної величини через певні (дискретні) проміжки часу; 2) дискретне представлення неперервної величини; 3) квантування.
22.	Дискретна модель – модель, у якій досліджуваний процес подають у вигляді дискретної послідовності подій.
23.	Діаграма – рисунок, що зображує співвідношення між певними величинами; умовне зображення числових величин або їх співвідношень, виконане геометричними побудовами.
24.	Дослідження операцій – комплексна математична дисципліна, що досліджує методами математичного моделювання пошук оптимальної стратегії.
25.	Екологія – наука про відношення рослинних і тваринних організмів і утворюваних ними співтовариств між собою та з навколишнім оточенням. Сучасна екологія, крім того, займається розробкою теоретичних і практичних методів контролю (моніторингу) стану навколишнього середовища.
26.	Електронна таблиця – інтерактивна система обробки даних, яка являє собою прямокутну таблицю, комірки якої можуть містити числові й рядкові типи даних або формули (якими задають залежність значення в даній комірці від вмісту інших комірок).
27.	Закон розподілу – див. Розподіл.
28.	Зворотний зв’язок – вплив вихідної величини деякої системи на вихід цієї самої системи. Може бути позитивним (віддаляє систему від стану рівноваги) і негативним (повертає систему до рівноваги).
29.	Змінна – програмний об’єкт, що має ім’я і значення, яке програма може отримати і змінити.
30.	Знакове моделювання – використання в якості моделі знакових перетворень будь-якого виду: схем, графіків, креслень, формул, наборів символів та інших умовних позначень.
31.	Значення – зміст, що присвоюється даному.
32.	Зображувальна точка – будь-яка точка на площині змінних х, v / ω, яка зображує стан системи, зокрема коливної.
33.	Інтерпретація 1) заг. – представлення, тлумачення; 2) інформат. – трансляція і виконання кожної команди початкової мови машинної програми.
34.	Інтерфейс – сукупність правил, що встановлюють єдині принципи взаємодії пристроїв ЕОМ.
35.	Інтерфейс користувача – програмні й апаратні засоби взаємодії оператора або користувача з програмою або комп’ютером.
36.	Інформатика – наука, що вивчає закони, методи і засоби нагромадження, обробки, збереження, передачі й представлення інформації.
37.	Інформаційна модель – 1) подання у відповідному вигляді процесу циркуляції інформації, що має бути автоматично оброблена в системі керування; 2) подання даних і відношень між ними математичними та програмними засобами; 3) формалізований опис інформаційних структур і операцій над ними.
38.	Інформація – відображення предметного світу з допомогою сигналів (знаків, символів, жестів, звуків тощо), міра (характеристика, ознака) розмаїтості довкілля (об’єктів у ньому).
39.	Кібернетика – наука про керування, а також про одержання, передавання і перетворення інформації в кібернетичних системах.
40.	Кібернетична система – сукупність зв’язаних одне з одним об’єктів (елементів системи), спроможних сприймати, зберігати, переробляти інформацію, а також обмінюватися інформацією.
41.	Коефіцієнти моделі – параметри математичної моделі, що є коефіцієнтами біля змінних
42.	Комп’ютерна модель – це інформаційна модель, реалізована засобами тієї чи іншої комп’ютерної технології.
43.	Комп’ютерне моделювання – моделювання об’єкта (процесу, явища) за допомогою програми, що реалізується обчислювальною системою.
44.	Комплекс – сукупність компонентів, що утворюють у певному розумінні єдине ціле.
45.	Константа – величина, що не змінює своє значення в процесі виконання алгоритму (програми).
46.	Концептуальна модель – змістова структура об’єкту з деякої предметної галузі.
47.	Концепція – набір основних ідей чи теоретичних положень, сукупність взаємопов’язаних уявлень, поглядів стосовно деякої проблеми.
48.	Кореляція (в матем. статистиці) – імовірнісна чи статистична залежність. На відміну від функціональної залежності кореляція виникає тоді, коли залежність однієї ознаки від іншої ускладнюється через наявність ряду випадкових факторів.
49.	Космологія – вчення про всесвіт у цілому.
50.	Критерій подібності – (основне поняття теорії подібності) безрозмірна комбінація фізичних величин – характеристик деякого явища, складена за певними правилами.
51.	Лінійчата діаграма – діаграма, що складається із сукупності горизонтальних смуг і використовується для демонстрування значень окремих груп даних.
52.	Логічна змінна – змінна, яка набуває одного з двох логічних значень – «істина» або «хиба».
53.	Логічна операція – 1) машинна операція, що реалізує функції алгебри логіки; 2) дія над логічними величинами з одержанням логічного значення.
54.	Математична екологія – сучасна наука, що поєднує математичні моделі й методи вирішення проблем екології.
55.	Математична модель – система математичних співвідношень, яка описує об’єкт, процес або явище.
56.	Математичне моделювання – процес побудови і дослідження математичних моделей різних явищ.
57.	Меню – відображуваний на екрані список команд, повідомлень, питань або варіантів відповідей, з яких користувач обирає потрібне, вводячи його номер, букву або вказуючи на нього курсором.
58.	Метод випадкової вибірки (метод Монте-Карло) – загальна назва обчислювальних методів, у яких використовується імовірнісна інтерпретація обчислюваних величин з допомогою випадкових чисел.
59.	Моделювання – особлива форма дослідження, що полягає у вивченні об’єкта не безпосередньо, а на його моделі.
60.	Модель – фізична система (або математичний опис), що відображає істотні властивості або характеристики об’єкта (процесу, явища).
61.	Мозковий штурм – оперативний метод колективного вирішення проблеми на основі стимулювання творчої активності, при якому учасникам обговорення пропонують висловлювати якомога більшу кількість варіантів розв’язання, в тому числі найфантастичніших. Далі із загальної кількості висловлених ідей відбирають найбільш вдалі, які можуть бути використані на практиці; є одним з методів експертного оцінювання.
62.	Надання (присвоювання) – призначення змінній деякого значення.
63.	Налагодження програми – виявлення, локалізація й усунення помилок у програмі.
64.	Натурний експеримент – експеримент з природним об’єктом.
65.	Обчислювальна математика – 1) розділ математики, що включає коло питань, пов’язаних з виконанням обчислень за допомогою ЕОМ; 2) теорія чисельних методів розв’язування типових математичних задач.
66.	Обчислювальна математика – розділ математики, що вивчає методи чисельного розв’язування математичних задач на ЕОМ.
67.	Обчислювальна система – сукупність апаратних засобів обчислювальної техніки і відповідного програмного забезпечення, яка функціонує як одне ціле і призначена для розв’язування певного класу задач.
68.	Обчислювальний експеримент – технологія теоретичних досліджень, заснована на вивченні поведінки і властивостей моделі за допомогою обчислювальної системи.
69.	Операнд – 1) величина у виразі, над якою виконується операція; 2) аргумент операції; частина машинної команди, що визначає об’єкт, над яким виконується операція.
70.	Оптимізація – 1) процес приведення системи в найкращий за даних умов (оптимальний) стан; 2) у досліджені операцій – знаходження екстремуму (максимуму або мінімуму) функції при заданих обмеженнях.
71.	Опція – параметр програми, що задає режим її роботи.
72.	Парадигма – система поглядів, закладена в конкретну технологію.
73.	Параметр – значення, надане змінній або на початку операції, або перед обчисленням виразу програмою.
74.	Подібність фізична – два фізичних процеси подібні, якщо вони якісно однакові, а їхні критерії подібності – попарно рівні. Тоді, знаючи значення величин, які характеризують один об’єкт (модель), можна знайти значення відповідних величин, що характеризують інший (оригінал).
75.	Полігон частот (у математичній статистиці) – один із способів графічного представлення щільності ймовірності випадкової величини. Є ламаною, яка сполучає точки, що відповідають серединним значенням інтервалів групування і частотам цих інтервалів.
76.	Поняття – цілісна сукупність суджень, в яких що-небудь стверджується про відмітні ознаки досліджуваного об’єкта.
77.	Популяція – це група особин одного виду, що існує на певному ареалі і характеризується багатьма спільними ознаками (народжуваність, смертність, тип росту, характер розподілення тощо).
78.	Постановка задачі – початковий етап процесу побудови моделі; на змістовому рівні передбачає виявлення всіх суттєвих факторів і зв’язків між ними і шуканим результатом.
79.	Похибка вимірювання – відхилення результатів вимірювання від дійсного значення вимірюваної величини.
80.	Похибка обчислень – методична помилка, що виникає при обчисленнях на ЕОМ.
81.	Предметна область – частина реального світу, що є середовищем визначення і реалізації конкретного процесу або групи процесів, що автоматизуються.
82.	Прикладна задача – задача, що має частковий, прикладний характер.
83.	Прикладна математика – математика в аспекті її додатків до розв’язання задач, постановка яких найчастіше не пов’язується з потребами самої математики.
84.	Принцип відповідності – твердження, згідно з яким нова теорія, що претендує на охоплення більш широкої області застосування, ніж попередня, має включати останню як граничний випадок.
85.	Програма – алгоритм, записаний мовою програмування, зрозумілою для ЕОМ.
86.	Псевдовипадкове число – число, частота повторення якого у вибраній послідовності визначається технікою використання випадкової вибірки з множини допустимих значень.
87.	Рекурентна формула – формула, що виражає наступні члени послідовності через попередні.
88.	Розподіл ймовірностей – одне з основних понять теорії ймовірностей і математичної статистики. Це функція, яка зіставляє з множиною можливих значень випадкової величини ймовірності цих значень.
89.	Середовище – оточення, в якому функціонує об’єкт.
90.	Середовище для моделювання – сукупність інструментальних засобів, що охоплює весь цикл розробки й функціонування моделі.
91.	Система – сукупність об’єктів і відношень між ними, яка утворює єдине ціле.
92.	Системний підхід – комплексний послідовний розгляд усіх факторів, шляхів і методів розв’язання задачі в їхньому взаємному зв’язку.
93.	Стійкість моделі – здатність обчислювального алгоритму не руйнуватися за певних значень вхідних даних.
94.	Стовпчаста діаграма – діаграма, що складається з вертикальних стовпців і використовується для подання значень величині їх зміни через певні проміжки часу.
95.	Стохастика – синонім до «теорія ймовірностей».
96.	Стохастична модель – математична модель, що містить випадкові (стохастичні) величини.
97.	Структурна схема – умовне зображення процесів, способів організації, аналізу чи схеми розв’язування задачі, за яким використовуються спеціальні графічні позначення для операцій, потоків даних, пристроїв.
98.	Таблиця – спосіб формалізованого подання даних у вигляді двовимірного масиву.
99.	Теорія – система основних ідей у тій або іншій галузі знань.
100.	Теорія подібності – вчення про умови подібності фізичних явищ; спирається на вчення про розмірності фізичних величин і слугує основою фізичного моделювання. Предметом теорії є встановлення критеріїв подібності для різноманітних фізичних явищ.
101.	Тестування моделі – етап створення моделі, полягає в тому, що обчислювальний експеримент спрямовують на підтвердження очевидних і заздалегідь відомих властивостей об’єкту.
102.	Технології 1) промислові – послідовність етапів перероблення природної сировини (руди, нафти тощо) або одержаних з неї напівфабрикатів (металів, комплектуючих до виробів); 2) соціальні – зміни, спрямовані на людину, на перетворення або набуття деяких її властивостей; ці технології за організацією і здійсненням значно складніші за промислові. Кінцевим результатом обох видів технологій є продукт із заданими властивостями.
103.	Точність – 1) міра можливості розрізняти майже рівні значення; 2) характеристика розрядності машинного подання чисел з рухомою крапкою; 3) атрибут даних, що визначає їх повну довжину і довжину дробової часини; 4) властивість програми видавати числові дані в межах припустимих відхилень.
104.	Траєкторія – лінія, яку описує тіло під час свого руху. Траєкторію, обмежену в просторі, називають фінітною (колова, еліптична на відміну від параболічної, гіперболічної).
105.	Тривіальний – позбавлений новизни, не оригінальний.
106.	Умова – правило для вибору однієї з альтернативних гілок алгоритму.
107.	Фазова площина – декартова система координат, в якій на вісі абсцис відкладають зміщення х, а на вісі ординат – його похідну, тобто швидкість руху v (краще величину v / ω).
108.	Фазова траєкторія – лінія, що її описує на фазовій площині (у фазовому просторі) зображувальна точка.
109.	Формалізація – процес подання інформації про об’єкт (процес, явище) у певній формі для формального виконавця.
110.	Функція – 1) змінна величина, значення якої залежить від значень іншої величини (величин); 2) одне з призначень пристрою, програми, системи; 3) у мовах програмування – процедура, внаслідок виконання якої формується деяке значення і виклик якої може бути використаний як операнд у виразі.
111.	Чисельні методи (матем.) – методи наближеного розв’язання математичних задач, що дозволяють звести розв’язання до скінченої кількості арифметичних дій над числами.
112.	Швидкодія – покажчик швидкості роботи ЕОМ та її продуктивності в одиницю часу.

1.	Абрамов С. А., Гнездилова Г. Г., Капустина Е. Н., Селюн М. И. Задачи по программированию. – М.: Наука, 1988.
2.	Авилов В. Физика + Математика + ЭВМ // Квант. – 1985. – № 11.
3.	Алминдеров В., Поповичева О. Международный турнир «Компьютерная физика» // Квант. – 1999. – № 3.
4.	Белонучкин В. Е. Кеплер, Ньютон и все-все-все... – М.: Наука, Гл. ред. физ.-мат. лит., 1990. 128 с. – (Б-чка ”Квант”; Вып. 78)
5.	Брудно А., Каплан Л. Московские олимпиады по программированию. – 2-е изд. – М.: Наука, 1990.
6.	Богданов К. Как быстрее спуститься на лифте в час пик. // Квант. – 2004. – № 1.
7.	Бурсиан Э. В. Задачи по физике для компьютера: Учеб. пособие для студ. физ.-мат. фак. пед. ин-тов. – М.: Просвещение, 1991.
8.	Верлань А. Ф., Распопов В. Б. Основы применения вычислительной техники: Пробное учебн. пособие для 10 кл. ср. шк. – К: Рад. шк., 1986.
9.	Вершинин О. Е. За страницами учебника информатики: Кн. для учащихся 10–11 кл. ср. шк. – М.: Просвещение, 1992.
10.	Вершинин О. Е. Компьютер для менеджера. – М. Высш. шк., 1990.
11.	Водолаженко А. В. Деловые применения компьютеров. (Раздел «Моделирование»). – Харьков: Харьковский педагогический университет, РЦ НИТ, 1994.
12.	Гильде В., Альтрихтер З. С микрокалькуляторм в руках: Пер. с нем. – 2-е изд. – М.: Мир, 1987. – 215 с. – (В мире науки и техники.)
13.	Глушков В. М., Валах В. Я. Что такое ОГАС? – М.: Наука, 1981.
14.	Горстко А. Б. Познакомьтесь с математическим моделированием. – М.: Знание, 1991.
15.	Гулд Х., Тобочник Я. Компьютерное моделирование в физике. Ч 1, 2. – М.: Мир, 1990.
16.	Жалдак М. И. Компьютер на уроках математики: Пособие для учителей. Издание 2-е, переработанное и дополненное. – К.: РУНЦ «ДИНИТ», 2004. – 327 с.
17.	Жалдак М. І. Про лінійне програмування. Сер. У світі математики, вип. 2. – К.: Радянська школа, 1970.
18.	Жалдак М. І., Рамський Ю. С. Чисельні методи математики: Посібник для самоосвіти вчителів. – К.: Радянська школа, 1984.
19.	Информатика: Энциклопедический словарь для начинающих / Сост. Д. А. Поспелов. – М.: Педагогика-Пресс, 1994.
20.	Інформатика та обчислювальна техніка: Короткий тлумачний словник / В. П. Гондюл, А. Г. Дерев’янко, В. В. Матвєєв, Ю. З. Прохур; За ред. проф. В. П. Гондюла. – К.: Либідь, 2000. – 320 с.
21.	Компьютеры, модели, вычислительный эксперимент. Введение в информатику с позиций математического моделирования / Авт. пред. А. А. Самарский. – М.: Наука, 1988.
22.	Лишевский В. П. Рассказы об ученых. – М.: Наука, 1986. – 168 с. (Серия «История науки и техники»).
23.	Кочергин А. Задача о слухах // Информатика и образование. – 1989. – № 5.
24.	Курицкий Б. Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: BHV – Санкт-Петербург, 1997.
25.	Марочник Л. С. Свидание с кометой. – М.: Наука. Гл. ред. физ.-мат. лит., 1985. 208 с. (Библиотечка “Квант”. Вып. 47)
26.	Математическое моделирование / Редакторы Дж. Эндрюс, Р. Мак-Лоун. – М.: Мир, 1979.
27.	Матюшкин-Герке А. Учебно-прикладные задачи в курсе информатики // Информатика и образование, 1992, №№ 3 – 6.
28.	Мичи Д., Джонстон Р. Компьютер-творец. – М.: Мир, 1987.
29.	Моисеев Н. Н. Математик задаёт вопросы… / Приглашение к диалогу /. – М.: Знание, 1974.
30.	Мышкис А. Д. Элементы теории математических моделей. – М.: Физматлит, 1994.
31.	Неуймин Я. Г. Модели в науке и технике. История, теория, практика. Л.: Наука, 1984. 189 с.
32.	Островская Е. М. Моделирование на компьютере. // Информатика и образование. – 1998. – №8.
33.	Пак В. В. Инженер, математик и другие: Простые методы математического моделирования природных и технологических процессов / Донецкий гос. техн. ун-т. – Донецк, 1995.
34.	Першиков В. И., Савинков В.М. Толковый словарь по информатике. – М.: Финансы и статистика, 1991. – 543 с.
35.	Простое и сложное в программировании / Авт. предисл. Е. П. Велихов. – М.: Наука, 1988.
36.	Распопов В. Б. Імітаційні алгоритми // Комп’ютер у школі та сім’ї. – 1999. – № 2.
37.	Румянцев А. Ю., Серветник Т. А. Астрономия: Учебно-методическое пособие / Под ред. А..В. Усовой. – Магнитогорск: МаГУ, 2003. – 309 с.
38.	Самарский А. А., Михайлов А. П. Компьютеры и жизнь (Математическое моделирование). – М.: Педагогика, 1987.
39.	Соколов И. М. Фракталы // Квант. – 1989. – № 5.
40.	Струве О., Линдс Б., Пилланс Э. Элементарная астрономия. – М.: Главн. ред. физ.-мат. лит., 1964. 468 с.
41.	Українсько–Англійсько–Німецько–Російський словник фізичної лексики. / упорядн. В. Козирський, В. Шендеровський. – К.: «Рада», 1996. – 934 с.
42.	Уолфрем С. Современный компьютер. / Сб. научно-популярных статей. Раздел “Научные исследования”. – М.: Мир, 1986.
43.	Федер Е. Фракталы. (Пер. с англ.) – М.: Мир, 1991.
44.	Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. – М.: Мир, 1967. – Т. 1. – 267 с.
45.	Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Задачи и упражнения с ответами и решениями. – М.: Мир, 1969. – 624 с.
46.	Физическая энциклопедия / Гл. ред. А.М. Прохоров. – М.: Сов. энциклопедия: В 4-х томах. – 1988.
47.	Хилькевич С. С., Зайцева О. А. Как построить траекторию? // Квант, 1987. – № 7.
48.	Хургин Я. И. Да, нет или может быть …– 2-е изд. – М.: Наука, 1983.
49.	Хургин Я. И. Ну и что? – М.: Молодая гвардия, 1970.
50.	Шнейдеров В. С. Занимательная информатика или … – СПб.: Политехника, 1994.
51.	Шпилевский А. Фрактальные кластеры // Информатика и образование. – 1989. – № 5.
52.	Эфрос А. Что такое теория протекания // Квант. – 1982. – № 2.