Ранговые коэффициенты корреляции

Ранжирование- это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.

Ранг- это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической из соответствующих номеров мест. Данные ранги называются связными.

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла. Эти коэффициенты могут быть использованы для определения тесноты связи, как между количественными, так и между качественными признаками.

Коэффициент корреляции рангов Спирмена основан на рассмотрении разности рангов значений факторного и результативного признаков:

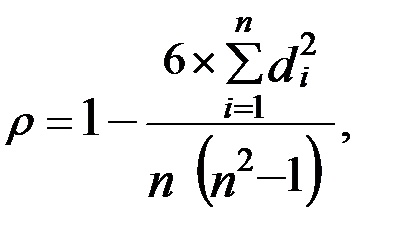
где - квадраты разности рангов; 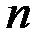- число наблюдений (число пар рангов), число «шесть» (даже в некоторых учебниках это число ошибочно заменено символом стандартного отклонения). Коэффициент Спирмена принимает любые значения в интервале . В основе коэффициента Спирмена лежит коэффициент корреляции.

Если переменная принимает несколько одинаковых значений, то им всем присваивают одинаковый ранг равный средней величине их мест в упорядоченном ряду. Например,

номер по порядку: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10;

: 1; 2; 2; 3; 4; 5; 5; 5; 7; 10;

ранг 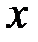: 1; 2,5; 2,5; 4; 5; 7; 7; 7; 9; 10.

Замечание. Вообще говоря в случае повторяющих чисел имеется уточненная формула.

При корреляция признается значимой с достоверностью 95%, если

.

Пример 1. 4.

По группе предприятий (табл. 1.9), выставивших акции на чековые аукционы в 2008 г., определить с помощью коэффициента Спирмена зависимость между величиной уставного капитала и количеством выставленных акций. Так как,

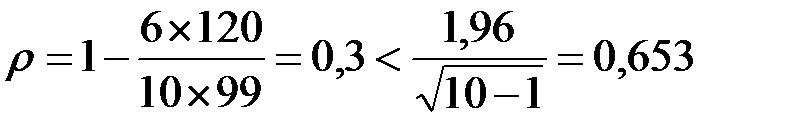
связь не установлена.

Таблица 1. 9

Расчет коэффициента Спирмена.

№ пред- приятия	Уставной капитал, млн. руб.	Число выставленных акций,	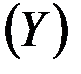Ранги	Разность рангов
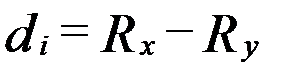
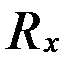
					-8
					-5
Итого

Ранговый коэффициент корреляции Кендалла также может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле:

где 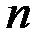- число наблюдений;

- сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Коэффициент изменяется от -1 до +1. Равенство 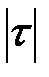=1 указывает на строгую линейную корреляцию.

При с достоверностью 95% наличие корреляции признается значимым, если

.

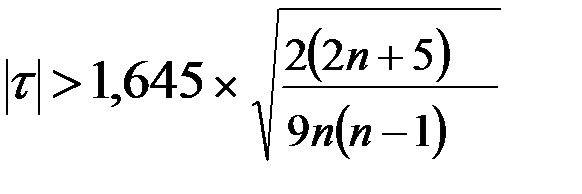Расчет данного коэффициента выполняется в следующей последовательности:

1. Значения 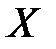ранжируются в порядке возрастания или убывания;

2. Значения 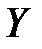располагаются в порядке, соответствующем значениям .

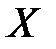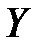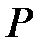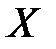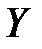3. Для каждого ранга определяется число следующих за ним значений рангов, превышающих его величину. Суммируя, полученные таким образом числа, находим , как меру соответствия последовательностей рангов по и . Величина 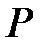учитывается со знаком (+);

4. Для каждого ранга 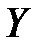определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через и фиксируется со знаком (-);

5. Определяется сумма баллов по всем членам ряда. В приведенном выше примере

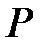= 1 + 8 + 1 + 6 + 4 + 3 + 3 + 2 +1 = 29;

= (-8) + 0 + (-6) + 0 + (-1) + (-1) + 0 + 0 + 0 = -16.

Таким образом:

,

что свидетельствует о практическом отсутствии связи между рассматриваемыми признаками.

Как правило, коэффициент Кендалла меньше коэффициента Спирмена. При достаточно большом объеме совокупности значения данных коэффициентов имеют следующую зависимость:

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) 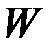(предложили Кендалл и Б. Смит), который вычисляется по формуле:

,

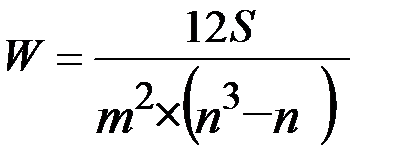где 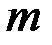- количество факторов, - число наблюдений, - отклонение суммы квадратов рангов от средней квадратов рангов.

При корреляция признается значимой с достоверностью 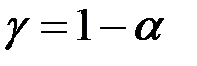, если

,

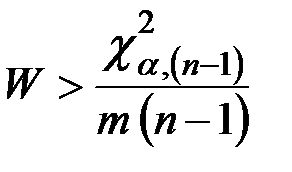где число степеней свободы.

Критические значения - статистики можно определить с помощью программы Microsoft Office Excel. Нажать , выбрать статистическую функцию ХИ2ОБР. Задать вероятность равную уровню значимости (например, 0,05 или 0,01) и число степеней свободы .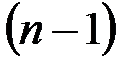

Ранговые коэффициенты Спирмена, Кендалла и конкордации имеют то преимущество, что с их помощью можно измерять и оценивать связи, как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.

Дата добавления: 2014-12-23