Методические указания. Вопросы для самопроверки

СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ И ПРОЦЕССОВ

Вопросы для самопроверки

1. Дайте определение динамического ряда.

2. Перечислите виды рядов динамики.

3. Что такое моментный ряд? Приведите примеры.

4. Что такое интервальный ряд? Приведите примеры.

5. С какой целью анализируются данные рядов динамики?

6. Какие показатели применяются для характеристики изменений уровней ряда динамики?

7. Какой вид средних величин используется для расчета среднего уровня моментного ряда динамики?

8. Как рассчитать средний темп роста и темп прироста уровней

ряда динамики?

9. Какие методы применяют для сглаживания уровней ряда?

10. Объясните термин «экстраполяция».

11. Объясните термин «тренд».

12. Какой вид средней применяется для нахождения среднего уровня интервального ряда динамики?

13. Какой вид средней применяется для нахождения среднего уровня моментного динамики?

ГЛАВА 3. ИНДЕКСНЫЙ МЕТОД АНАЛИЗА

Приступая к изучению темы, следует ознакомиться с общим понятием индекса, который может выступать как показатель изменения явлений не только во времени, но и в пространстве (территориальные индексы). Важно знать основные задачи, которые решаются с помощью индек­сов (индексного метода): обеспечение сопоставимости непосредст­венно несоизмеримых, разнородных в натуральном выражении элементов совокупности с помощью универсальных для них единиц измерения (весов), а также факторный анализ изменения получа­емых в результате этого показателей.

Следует изучить основные виды индексов (индивидуальные, сводные, переменного и постоянного состава), а также способы построения сводных индексов с помощью средней в агрегатной, арифметической или геометрической формах в зависимости от имеющихся данных. Да­лее необходимо рассмотреть методы разложения сводных индексов на субиндексы по факторам для случаев их независимого или по­следовательного изменения (воздействия).

В заключение следует ознакомиться с порядком построения балансов отклонений обобщающих показателей в зависимости от факторных показателей в абсолютном и относительном выражении, способами анализа и оценки таких балансов, выбора оптималь­ного изменения обобщающего показателя.

§ 3.1. Общие понятия

Индекс – относительная величина, получаемая в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или с планом.

Обычно сопоставляемые показатели характеризуют явления, состоящие из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости. Например, промышленные предприятия выпускают разнообразные виды продукции. Общий объем продукции предприятия нельзя получить суммированием количества различных видов продукции в натуральном выражении (например, нельзя складывать количества продукции, выраженные в килограммах и кубических метрах). В качестве меры соизмерения количества разнородных продуктов можно использовать цену, себестоимость или трудоемкость единицы продукции.

В развитии индексной теории в России сложились два направления: синтетическое и аналитическое. Обобщающее или синтетическое направление трактует индекс как показатель среднего изменения уровня изучаемого показателя. В аналитической теории индексы – это показатели изменения уровня результативной величины под влиянием изменения индексируемой величины. Например, величина индекса цен продукции, равная 1,154 может быть истолкована в обобщающем значении как величина, указывающая на то, что цены на продукцию возросли в целом на 15,4% или в 1,154 раза, а в аналитическом значении как показатель того, что в связи с изменением цен стоимость продукции (или размер выручки) увеличилась на 15,4%.

С помощью индексных показателей решаются следующие задачи:

1) характеристика общего изменения сложного экономического показателя (например, затрат на производство продукции, стоимости произведенной продукции и т.д.) или формирующих его отдельных показателей-факторов;

2) выделение в изменении сложного показателя влияния одного из факторов путем элиминирования влияния других факторов (например, увеличение выручки от реализации продукции, связанное с ростом цен или выпуска продукции в натуральном выражении). В качестве самостоятельной можно выделить задачу обособления влияния изменения структуры явления на индексируемую величину (например, при изучении динамики среднеотраслевой себестоимости продукции исследуется влияние изменения в распределении объемов выпуска продукции по предприятиям отрасли).

Способы построения индексов зависят от содержания изучаемых показателей, методологии расчета исходных статистических показателей, имеющихся в распоряжении исследователя статистических данных и целей исследования.

Для удобства восприятия индексов в теории статистики разработана определенная символика. Каждая индексируемая величина имеет свое символическое обозначение. Например, количество единиц данного вида продукции обозначается q, цена единицы изделия- p, себестоимость единицы изделия – z, трудоемкость единицы изделия – t и т.д.

По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы.

§ 3. 2. Индивидуальные индексы

Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности. Индивидуальный индекс обозначается 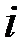.Расчеты индивидуальных индексов просты и выполняются путем вычисления соотношения индексируемой величины, взятой при различных условиях (например, за отчетный и за базисный периоды). Период, с которым производится сравнение, называется базисным. Сравниваемый период называется текущим или отчетным. Данные базисного периода обозначают подстрочным значком «0», а отчетного- «1». Индексы принято вычислять с точностью до 0,001 или до 0,1%.

Пример 3. 1. Рассмотрим вычисление индивидуальных индексов.

Рассчитаем по приведенным данным (табл. 3.1) индивидуальные индексы, т.е. показатели изменения количества произведенной продукции и изменение цен по каждому виду продукции. Для этого надо данные о количестве каждого вида продукции и их ценах отчетного периода выразить в процентах и коэффициентах к соответствующим данным базисного периода.

Таблица 3. 1

Количество выработанной продукции и цены за два периода

Виды изде-лий	Единица измере-ния	Количество продукции, произведенной в базисном периоде, q0	Цена единицы в базисном периоде, руб., p0	Количество продукции, произведенной в отчетном периоде, q1	Цена единицы в отчетном периоде, руб., p1
А Б В	шт. кг м				9,5 10,0 5,0

Индивидуальный индекс количества продукции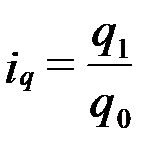

Индивидуальный индекс цен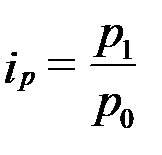

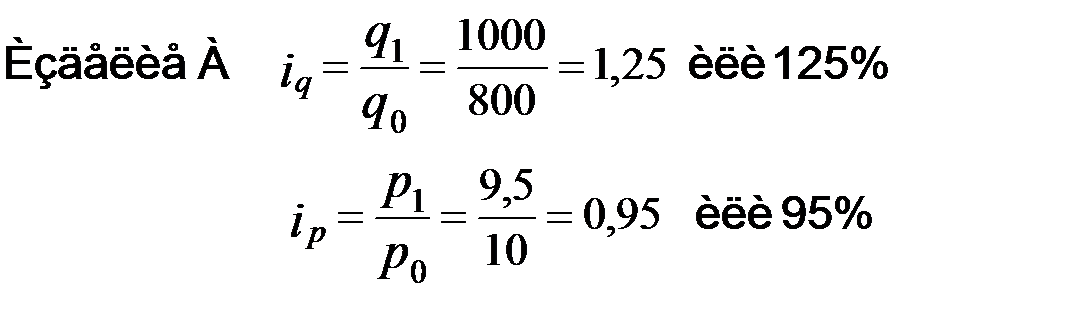
Продукции вида А в отчетном периоде произвели больше в 1,25 раза или на 25% (125% - 100% = 25%). Цены на продукцию вида А выросли в 0,95 раза (т.е. снизились) или снизились на 5% (95% - 100% = -5%).

Продукции вида Б в отчетном периоде произвели больше в 1,1 раза или на 10% (110% - 100% = 10%). Цены на продукцию вида Б выросли в 1,25 раза или на 25% (125% - 100%) = 25%.

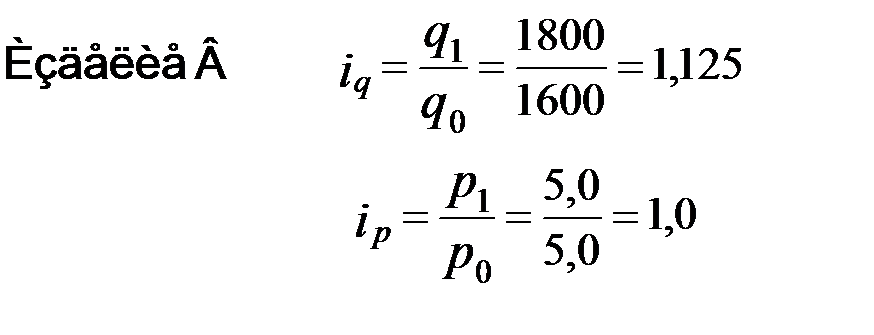
Продукции вида B в отчетном периоде произвели больше в 1,125 раза или на 12,5% (112,5% - 100% = 12,5%). Цены на продукцию вида В выросли в 1,0 раза (т.е. не изменились) или изменение цен равно 0% (100% - 100%) = 0%.

Индивидуальные индексы могут исчисляться в виде индексного ряда за несколько периодов. При этом существуют два способа расчета индивидуальных индексов: цепной и базисный.

При цепном способе расчета за базу отношения принимается индексируемая величина соседнего прошлого периода. В этом случае база расчета в ряду постоянно меняется. Например, цепной индивидуальный индекс количеств:

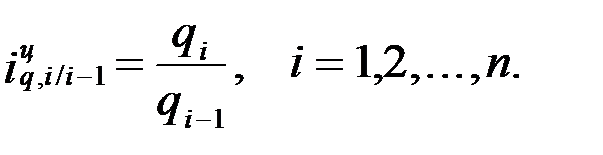
При базисном способе расчета за базу отношения принимается индексируемая величина какого-либо одного периода. В этом случае база расчета в ряду остается постоянной. Например, базисный индивидуальный индекс количеств:

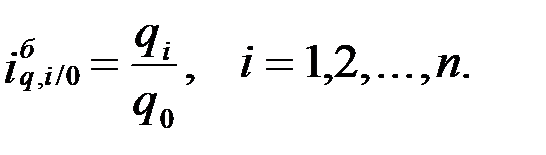
Произведение цепных индексов дает базисный индекс:

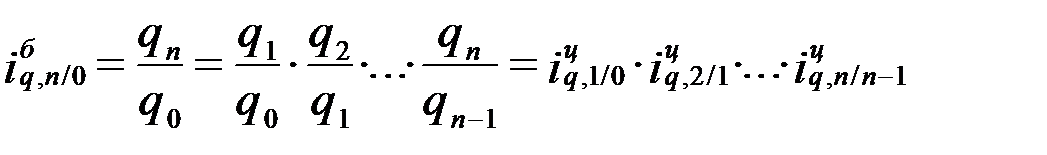
Пример 3. 2.

Рассмотрим расчет индивидуальных цепных и базисных индексов.

Таблица 3. 2

Количество продукции

Год
Количество продукции, тыс.шт.	40,0	38,0	37,5	36,0	38,2	40,2

Индивидуальные цепные индексы:

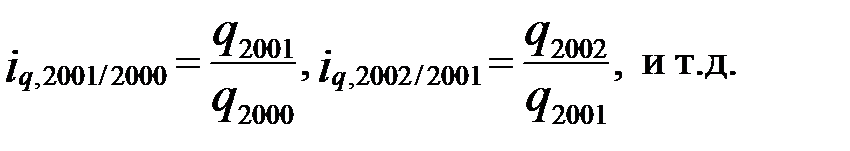
Индивидуальные базисные индексы рассчитаем для базового периода 2000 года:

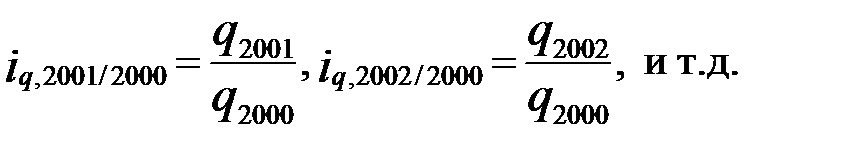
Результаты сведем в табл. 3.3.

Таблица 3. 3

Индивидуальные цепные и базисные индексы

Год
Индексы цепные	-	0,950	0,987	0,960	1,061	1,052
Индексы базисные	-	0,950	0,938	0,900	0,955	1,005

§ 3. 3. Общие индексы

Сводный или общий индекс отражает изменение по всей совокупности элементов сложного явления. Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми, или субиндексами. Например, общий индекс характеризует динамику объема промышленной продукции. К субиндексам в этом случае могут быть отнесены индексы продукции по отдельным отраслям промышленности. Обозначают сводный (общий) индекс символом 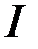. В зависимости от содержания и характера индексируемой величины различают индексы количественных (объемных) показателей (например, индекс физического объема продукции) и индексы качественных показателей (например, индексы цен, себестоимости).

Рассмотрим общие индексы количественных показателей.

Особые приемы построения индексов количественных показателей используют, когда итоги по отдельным элементам несоизмеримы. Различные виды продукции неравноценны по количеству затраченного на них общественного труда и имеют разные потребительные стоимости и различные натуральные единицы измерения. Для получения общего итога необходимо данные по различным видам продукции привести к единой, общей мере. Например, использовать стоимостную оценку продукции. Стоимостную оценку экспорта продукции. Тогда вместо 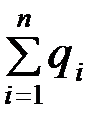получим суммы вида 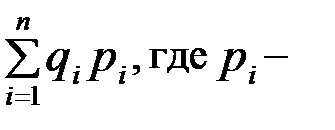цена единицы продукции данного вида, 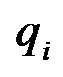- количество продукции 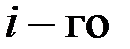вида в натуральном выражении, 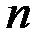- общее число видов продукции.

Такой переход от одних единиц измерения к другим в теории индексов называют соизмерением. При построении индексов количественных (объемных) показателей в качестве соизмерителей применяют те или иные качественные показатели. Например, цену, себестоимость или трудоемкость единицы изделия. Выбор коэффициента соизмерения зависит от цели исследования.

Тогда стоимость всей продукции, выработанной на предприятии в базисном периоде будет равна:

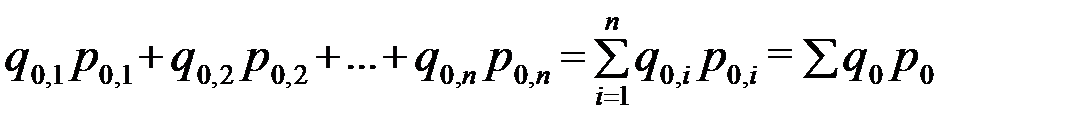
(для упрощения записи, подстрочный значок «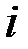» по которому идет суммирование не указывают). Стоимость продукции отчетного периода составит:

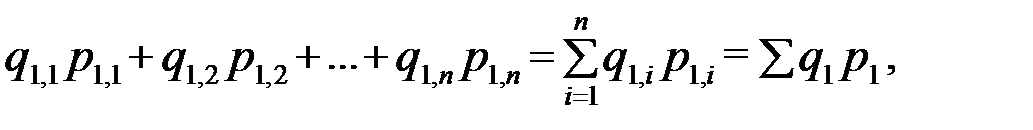
где 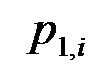- цена продукции 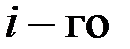вида в отчетном периоде; 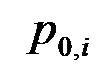- цена продукции 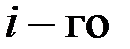вида в базисном периоде; 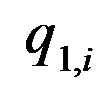- количество продукции 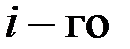вида в отчетном периоде; 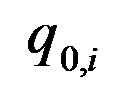- количество продукции 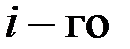вида в базисном периоде;

Если разделить стоимость продукции отчетного периода на стоимость продукции базисного периода, получим индекс стоимости продукции:

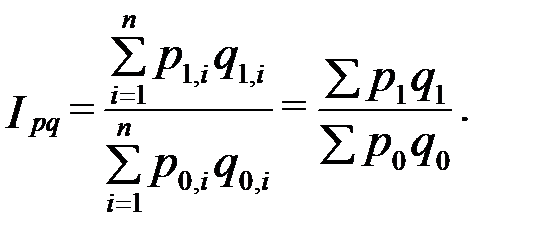
Данный индекс характеризует изменение стоимости продукции, которое зависит от изменения уровня цен и количества выпускаемой продукции в отчетном периоде по сравнению с базисным.

Индекс стоимости не дает представления об изменении количества выпускаемой продукции. Устраним влияние изменения цен, для чего количество продукции, произведенной в отчетном и базисном периодах, умножим на одинаковые для обоих периодов цены:

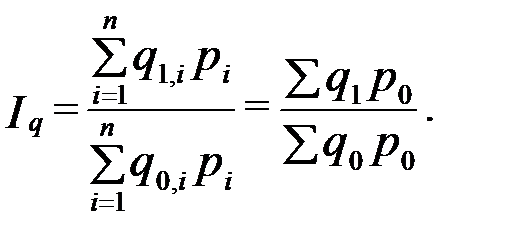
Такой индекс называют агрегатным индексом физического объема.

При вычислении индекса физического объема продукции возможны разные решения в зависимости от выбора коэффициента соизмерения.

Если принять за коэффициент соизмерения цены базисного периода, то индекс физического объема продукции будет иметь следующий вид:

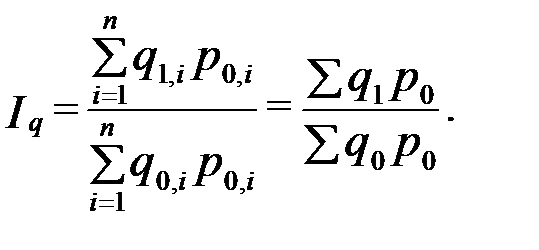
Такой вариант построения агрегатного индекса был предложен Э.Ласпейресом в 1864 г. Обычно в задачах по теории статистики индексы количественных показателей вычисляются с базисными весами, то есть в форме Ласпейреса.

Пример 3. 3.

Таблица 3. 4

Реализация овощей на рынке

Наименование товара	Базисный период	Отчетный период
Количество	цена за 1 кг, руб.	Количество	цена за 1 кг, руб.
Картофель, т
Морковь, ц

Индекс физического объема:

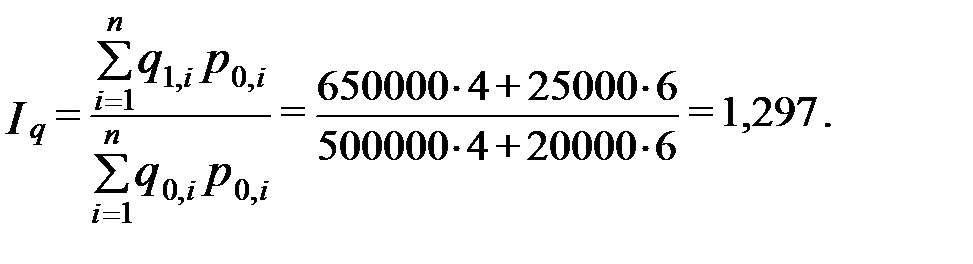
Следовательно, объем реализованной массы в неизменных ценах увеличился на 29,7%.

Вычитая из числителя индекса физического объема его знаменатель, получим прирост товарооборота за счет изменения физического объема продукции .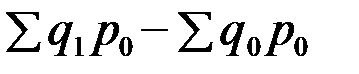

По данным задачи получим:

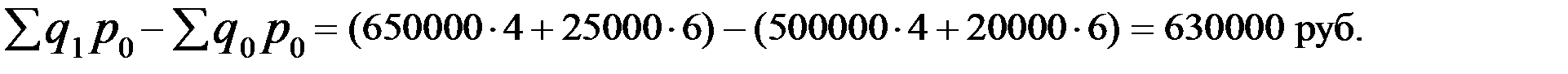Особенностью агрегатного индекса является то, что в числителе и в знаменателе меняется индексируемая величина, значения же другой, являющейся соизмерителем, остаются неизменными.

Если в качестве соизмерителей использовать цены отчетного периода, то индекс физического объема продукции примет вид:

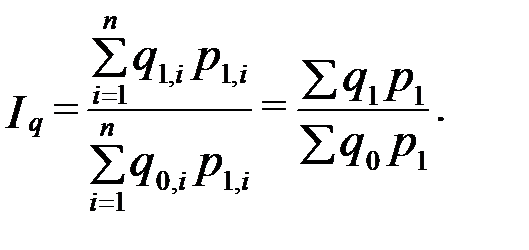
Агрегатный индекс с соизмерителями отчетного периода был предложен в 1874 г. Г. Пааше.

Основываясь на формулах Пааше и Ласпейреса, И. Фишер предложил рассчитывать среднюю геометрическую из двух агрегатных индексов, назвав ее «идеальной формулой»:

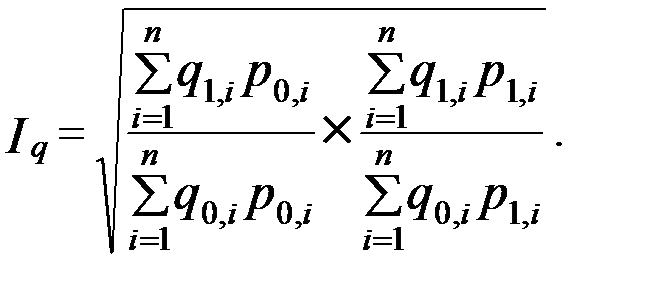
«Идеальность» формулы заключается в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный «обратный» индекс- это обратная величина к величине первоначального индекса, т.е.

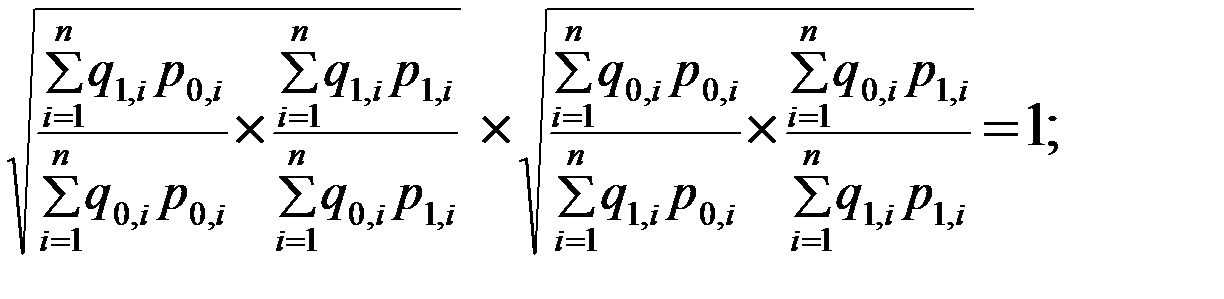
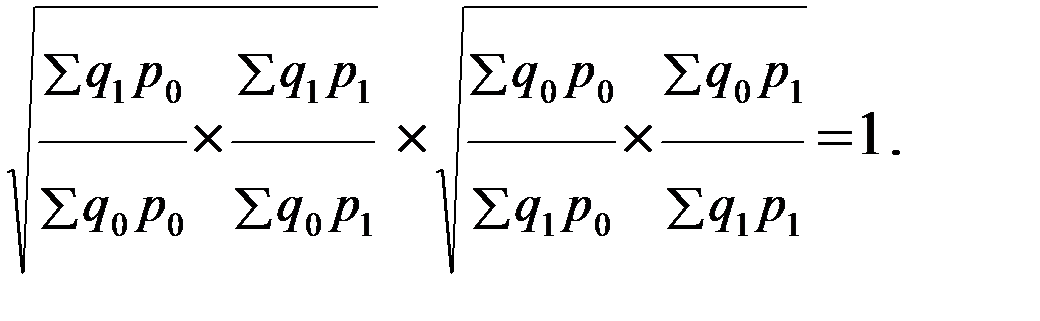
§ 3. 4. Общий индекс физического объема как средняя арифметическая величина из индивидуальных индексов

Пусть известна стоимость продукции каждого вида в базисном периоде 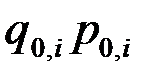и индивидуальные индексы физического объема .

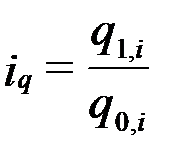Исходной базой построения среднего из индивидуальных индексов служит агрегатная форма индекса Ласпейреса

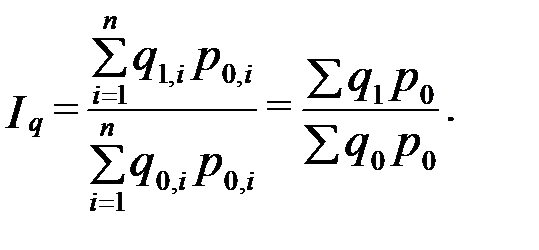
Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:

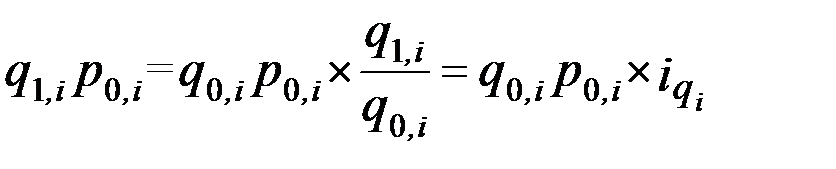
Тогда формула агрегатного индекса физического объема принимает вид:

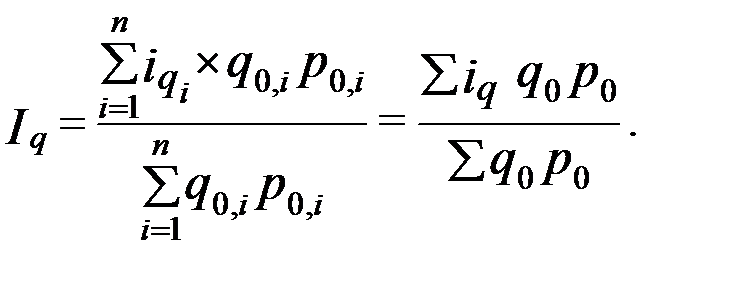
т.е. получим средний арифметический индекс физического объема, где весами служат стоимости отдельных видов продукции в базисном периоде. При выборе весов следует иметь в виду, что средний индекс должен быть тождествен агрегатному, который является основной формой индекса.

Учитывая, что отношение 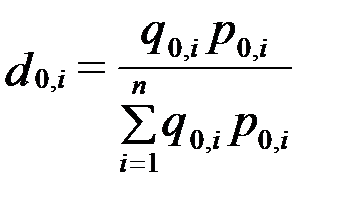характеризует долю данного вида продукции в объеме стоимости всей продукции базисного периода, средний арифметический индекс физического объема будет иметь вид: .

Пример 3. 4.

Таблица 3. 5

Продажа товаров в розничной торговле

Группы товаров	Товарооборот, млн. руб.	Изменение количества, проданных товаров, %
базисный период	отчетный период
Обувь			+15
Трикотажные изделия			+30

Определим общий индекс физического объема товарооборота, используя средний арифметический индекс. Согласно условию, индивидуальные индексы физического объема товарооборота по отдельным видам товаров равны:

Обувь ;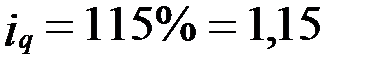

Трикотажные изделия .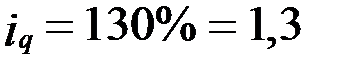

Тогда получим:

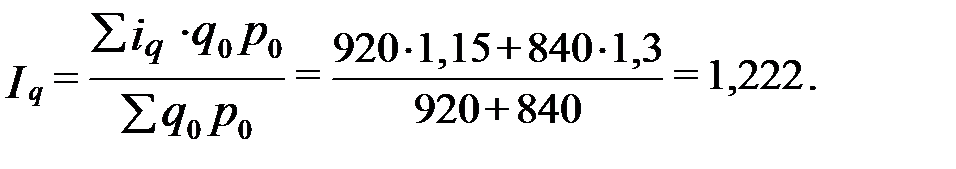
Имеет место рост физического объема реализации на 22,2%.

Общий индекс физического объема продукции не всегда может быть представлен средней величиной из индивидуальных индексов. Этого нельзя сделать в том случае, когда номенклатура изделий в текущем периоде не совпадает с их номенклатурой в базисном периоде, т.е. средние индексы могут быть рассчитаны лишь по сравнимому кругу изделий.

§ 4. 5. Индексы качественных показателей

Наряду с индексами физического объема продукции широко применяются индексы качественных показателей: цен, себестоимости, производительности труда, средней заработной платы и т.д. Качественный показатель характеризует уровень изучаемого результативного показателя в расчете на количественную единицу и определяется как отношение данного результативного показателя к связанному с ним количественному показателю (фактору), на единицу которого он определяется. Например, себестоимость единицы продукции определяется как отношение суммы затрат на производство этого вида продукции к количеству единиц продукции данного вида; средняя заработная плата определяется делением фонда заработной платы на численность работников и т. д.

Формулы индексов качественных показателей рассмотрим на примере расчета индексов цен.

Индивидуальные индексы цен характеризуют относительное изменение уровня цен единицы каждого вида продукции в отчетном периоде по сравнению с базисным 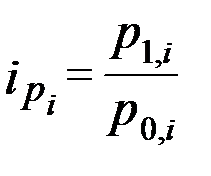. Расчет индивидуальных индексов цен был рассмотрен выше.

Для определения общего изменения уровня цен на продукцию предприятия, включающую различные виды, нужно рассчитать агрегатный индекс цен. Непосредственное суммирование уровня цен разнородной продукции не имеет экономического содержания. Несоизмеримость уровней в таком случае устраняется путем взвешивания цены каждого вида продукции на количество произведенных единиц. Чтобы сравнение отражало только изменение цен, необходимо, чтобы количество продукции фиксировалось в числителе и знаменателе индекса цен на уровне одного из периодов.

Общая формула агрегатного индекса цен записывается так:

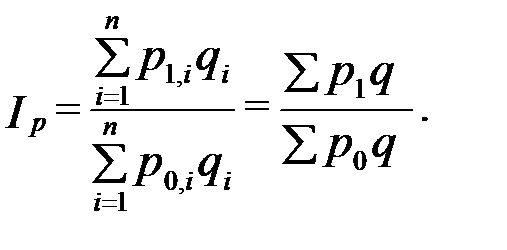
Как и в случае построения агрегатных индексов физического объема, возможен выбор в качестве веса количества продукции отчетного периода (формула Пааше) или количества продукции базисного периода (формула Ласпейреса). Формула агрегатного индекса цен Ласпейреса:

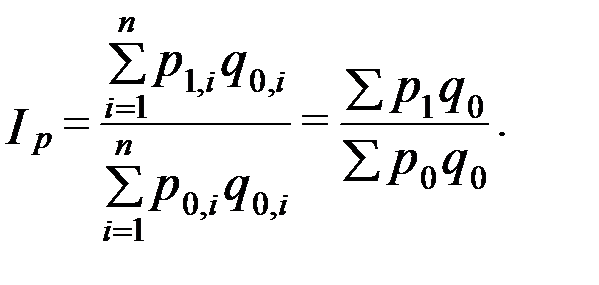
Формула агрегатного индекса цен Пааше:

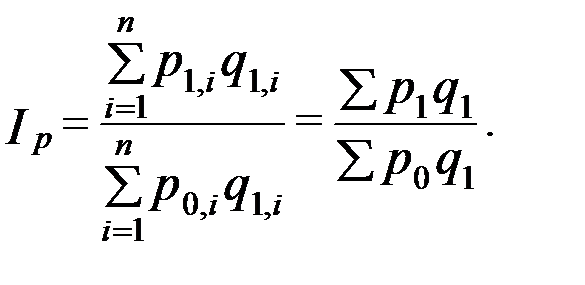
Обычно в задачах по общей теории статистики индексы качественных показателей вычисляются с отчетными весами, то есть в форме Пааше.

Пример 3. 5. Рассмотрим расчет индекса цен (табл. 3.6).

Индекс цен (Пааше):

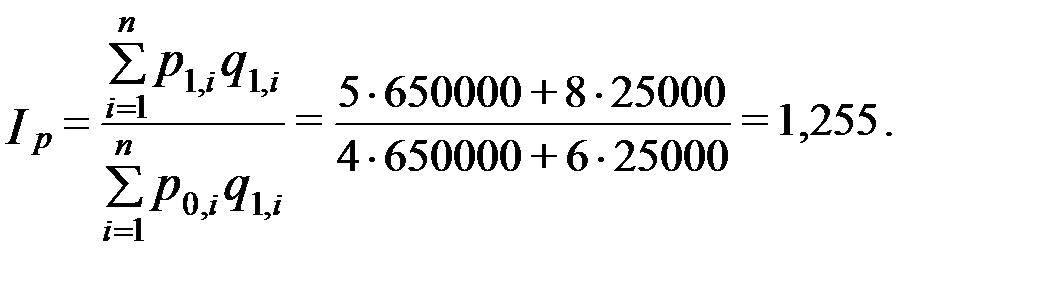
Следовательно, цены выросли в среднем на 25,5% (125,5%-100,0%).

Таблица 3. 6

Реализация овощей на рынке

Наименование товара	Базисный период	Отчетный период
Количество	цена за 1 кг, руб.	Количество	цена за 1 кг, руб.
Картофель, т
Морковь, ц

Вычитая из числителя индекса цен его знаменатель, получим прирост товарооборота за счет изменения цен .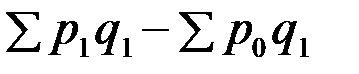

По данным предыдущей задачи получим:

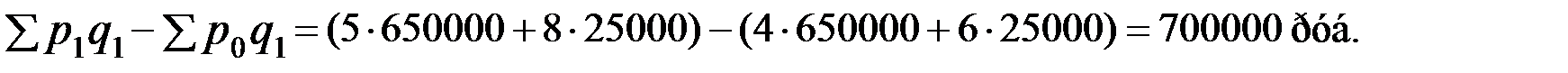
Система индексов строится так, что индекс товарооборота можно исчислить на основе индекса цен и индекса физического объема по формуле:

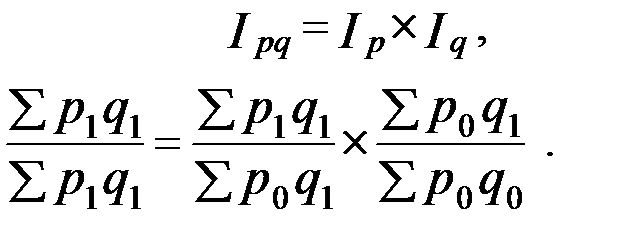
При этом индекс цен вычисляется по методу Пааше, а индекс физического объема по методу Ласпейреса.

Исчислим индекс товарооборота по данным предыдущего примера 7.5:

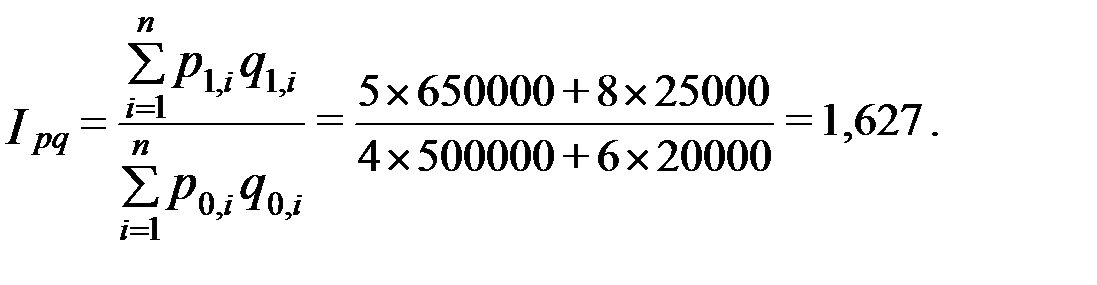
Товарооборот увеличился в 1,627 раза или на 62,7% (162,7%-100%).

Проверим увязку индексов в систему. Отметим, что все индексы вычислялись с точностью до трех знаков после запятой, поэтому равенство выполняется с точностью до нескольких тысячных

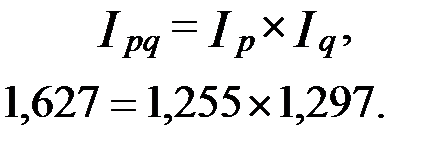
§ 3.6. Средний гармонический индекс

качественных показателей

В статистике торговли широко применяется средний взвешенный гармонический индекс при определении индексов розничных цен. Учет товарооборота ведется в денежном выражении по группам товаров, данные же о количестве проданных товаров в натуральном выражении во многих случаях отсутствуют. Поэтому непосредственно определить условную сумму товарооборота 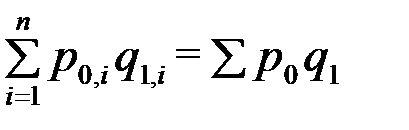невозможно и тогда вместо агрегатной формы индекса Пааше вычисляется средний гармонический индекс с текущими весами

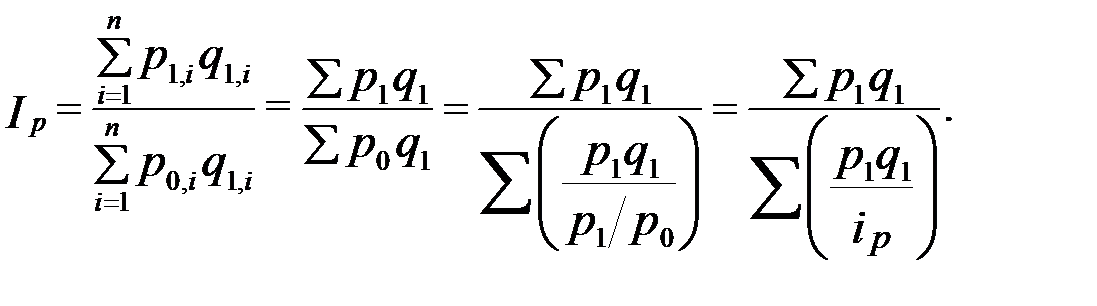
Он алгебраически тождествен формуле Пааше и имеет точно такое же экономическое содержание.

Пример 3. 6.

В отчетном году было продано хлопчатобумажных тканей на 20 млн. руб., шелковых – на 15 млн. руб. и шерстяных – на 30 млн. руб. Исчислите общий индекс цен на эти товары, если известно, что цены были повышены на хлопчатобумажные ткани на 6%, на шелковые ткани на 4% и на шерстяные ткани на 10%.

Решение.

Согласно условию индивидуальные индексы цен равны:

Хлопчатобумажные ткани ;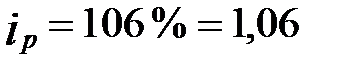

Шелковые ткани ;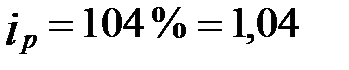

Шерстяные ткани .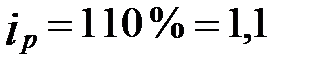

Тогда получим,

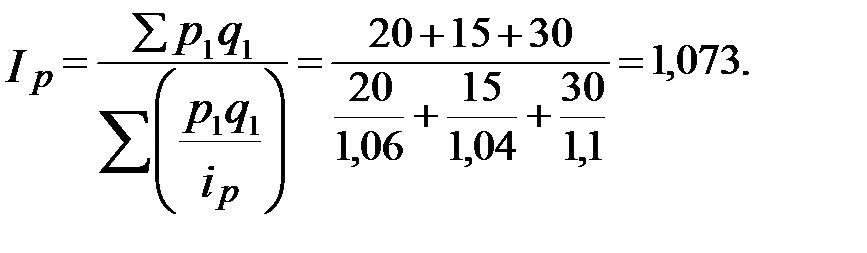
Цены повысились в 1,073 раза или на 7,3% (107,3% - 100%).

В данном случае агрегатный индекс цен представлен в форме среднего гармонического взвешенного индекса. В качестве весов используются фактические объемы товарооборота в отчетном месяце.

§ 3.7. Индексы переменного и постоянного состава.

Дата добавления: 2014-12-23