Методические указания. Вопросы для самопроверки

Вопросы для самопроверки

1. Какая связь называется функциональной?

2. Какая связь называется корреляционной?

3. Какие признаки называются факторными и результативными?

4. В каких пределах изменяется линейный коэффициент корреляции?

5. Как по коэффициенту корреляции определить тесноту и направление связи?

6. Что показывает коэффициент эластичности?

7. В каких пределах изменяется индекс корреляции? Что он показывает?

8. Какая дисперсия характеризует вариацию результативного признака, связанную с вариацией фактор­ного признака, положенного в основу аналитической группировки?

9. Что показывает коэффициент детерминации и как он связан с коэффициентом корреляции?

10. Какая существует связь между линейным коэффициентом

корреляции и коэффициентом регрессии уравнения парной линейной регрессии?

11. С помощью, каких показателей исследуется взаимосвязь качественных признаков?

12. Связь, каких признаков исследуют с помощью ранговых коэффициентов корреляции?

13. Какая дисперсия характеризует вариацию результативного признака, связанную с вариацией фактор­ного признака, положенного в основу аналитической группировки.

14. Какая дисперсия характеризует вариацию результативного признака, связанную с вариацией всех факторных признаков, кроме группировочного, положенного в основу аналитической группировки?

15. Какие виды связей выделяют по аналитическому выражению?

16. Какие виды связей выделяют по форме проявления взаимосвязей.

ГЛАВА 2. РЯДЫ ДИНАМИКИ И ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ

Приступая к изучению темы, следует ознакомиться с содержани­ем понятия ряда динамики. Прежде всего, ряд динамики представ­ляет собой последовательность изменений с течением времени значений определенного обобщающего показателя (уровней ряда) некоторого массового явления (статистической совокупности). Этот обобщающий показатель может быть также рассмотрен как при­знак этого массового явления, а ряд динамики – как статистическая совокупность изменений значений этого признака (процесса) с тече­нием времени. С этой точки зрения ряд динамики представляет собой определенную эмпирическую реализацию (траекторию) возможных значений соответствующего случайного процесса за данный период времени.

Далее следует рассмотреть основные виды рядов динамики (моментные и интервальные), изучить основные их показатели: абсолютные (приросты), относительные (темпы роста, прироста), средние (арифметические, геометрические, хронологические, скользящие и др.).

Затем необходимо изучить понятие тенденции ряда динамики, методы обработки рядов динамики, метод скользящей средней, аналитическое сглаживание, выбор уравнения для аналитического сглаживания, расчет параметров уравнения, элементы интерполяции и экстраполяции динамических рядов.

И, наконец, рассмотреть сезонные колебания, индексы сезонности и сезонные волны.

§ 2.1. Общие понятия

Важной задачей статистики является изучение изменений анализируемых показателей во времени. Эти изменения можно изучать, если иметь данные за ряд моментов или промежутков времени, следующих друг за другом.

Прогнозирование – это оценка будущего на основе всестороннего анализа тенденций развития социально-экономических явлений и их взаимосвязей. Процесс прогнозирования предполагает выявление возможных альтернатив развития в перспективе для обоснованного их выбора и принятия оптимального решения.

Прогнозирование ведется на основе глубокого анализа широкого спектра информации. Но первоначальный этап прогнозирования всегда связан с анализом временных рядов, который позволяет охарактеризовать закономерность изменения явления во времени.

Ряд расположенных в хронологической последовательности значений статистических показателей, представляет собой временной (динамический) ряд. Временной ряд состоит из двух элементов:

1) указываются моменты или периоды времени, к которым относятся приводимые статистические данные;

2) приводятся статистические показатели, которые характеризуют изучаемый объект на определенный момент или за указанный период времени.

Статистические показатели, характеризующие изучаемый объект, называют уровнями ряда. Статистические показатели, приводимые в динамическом ряду, могут быть абсолютными, относительными или средними величинами. Если уровни динамического ряда, представляют собой результат накопленный за определенный промежуток времени то ряд называется интервальным. Если уровни этого ряда относятся к определенной дате, то такой ряд динамики называется моментным динамическим рядом.

Отличительной особенностью интервальных рядов динамики абсолютных величин является возможность суммирования их уровней. В результате суммирования уровней интервального динамического ряда получим накопленные итоги, которые имеют реальное содержание. Сумма уровней моментного ряда динамики не имеет никакого реального содержания.

Ряды динамики относительных и средних величин состоят из производных статистических показателей, полученных в результате сопоставления между собой суммарных абсолютных данных. Рядом динамики относительных величин называется ряд цифровых данных, характеризующих изменение относительных размеров изучаемых явлений во времени. Рядом динамики средних величин называется ряд цифровых данных, характеризующих изменение среднего размера признака во времени.

§ 2.2. Показатели ряда динамики и методы их исчисления

К числу основных задач, возникающих при изучении динамических рядов, относятся следующие:

1) характеристика интенсивности изменений в уровнях ряда от периода к периоду или от даты к дате;

2) определение средних показателей временного ряда за тот или иной период;

3) выявление основных закономерностей динамики исследуемого явления на отдельных этапах и в целом за рассматриваемый период;

4) выявление факторов, обусловливающих изменение изучаемого объекта во времени;

5) прогноз развития явления на будущее.

Динамический ряд представляет собой ряд последовательных уровней, сопоставляя которые между собой можно получить характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики, к числу которых относятся абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста. Если сравнению подлежат несколько последовательных уровней, то возможны два варианта сопоставления:

1) каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения. В качестве базисного уровня выбирается либо начальный уровень динамического ряда или же уровень, с которого начинается какой-то новый этап развития явления. Такое сравнение называется сравнением с постоянной базой.

2) Каждый уровень динамического ряда сравнивается с непосредственно ему предшествующим, такое сравнение называют сравнением с переменной базой.

Показатели динамики с постоянной базой (базисные показатели) характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (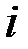 -го) периода. Показатели динамики с переменной базой (цепные показатели) характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени. Уровни динамического ряда будем обозначать как .

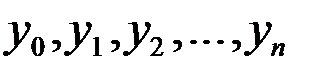Абсолютный прирост определяется как разность между двумя уровнями динамического ряда и показывает на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:

,

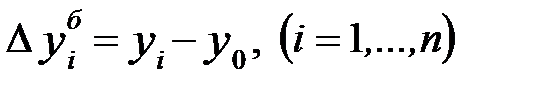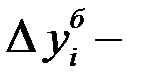базисный абсолютный прирост,

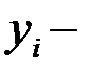уровень сравниваемого периода,

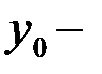уровень базисного периода.

При сравнении с переменной базой абсолютный прирост будет равен:

,

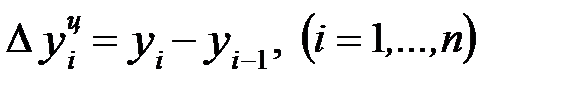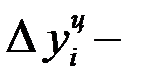базисный абсолютный прирост,

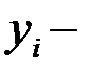уровень сравниваемого периода,

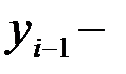уровень непосредственно предшествующего периода.

Абсолютный прирост с переменной базой иначе называют скоростью роста.

Коэффициент роста определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень базисного периода.

При сравнении с постоянной базой .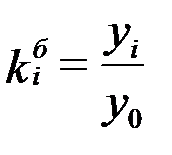

При сравнении с переменной базой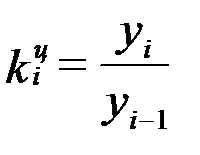

Если коэффициенты роста выражают в процентах, то их называют темпами роста:

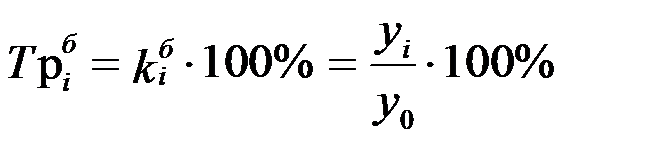или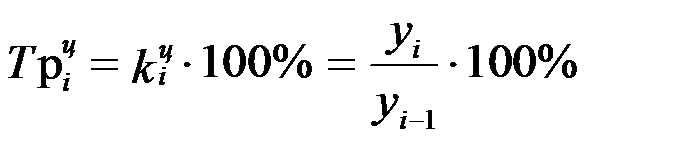

Темп прироста показывает на сколько процентов уровень данного периода больше (или меньше) базисного уровня.

При сравнении с постоянной базой:

.

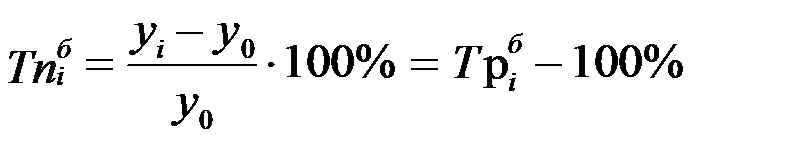При сравнении с переменной базой:

.

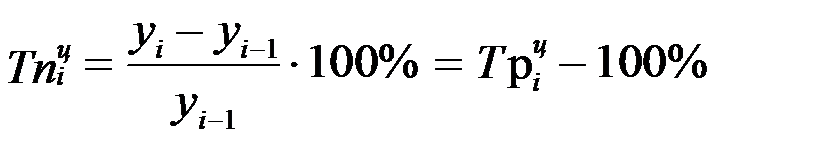Существует взаимосвязь между показателями динамики, вычисленными с постоянной и переменной базой. Так, сумма абсолютных приростов с переменной базой дает общий прирост за исследуемый период:

.

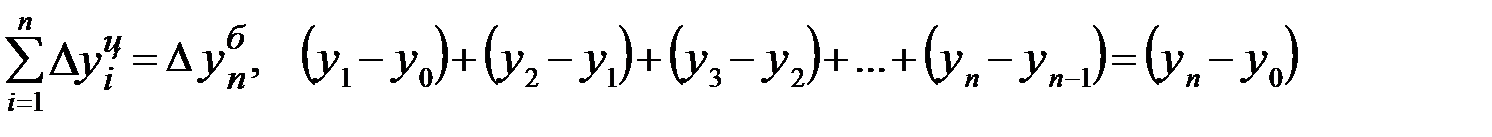При наличии коэффициентов роста с переменной базой соответствующий базисный коэффициент роста находится перемножением цепных коэффициентов роста:

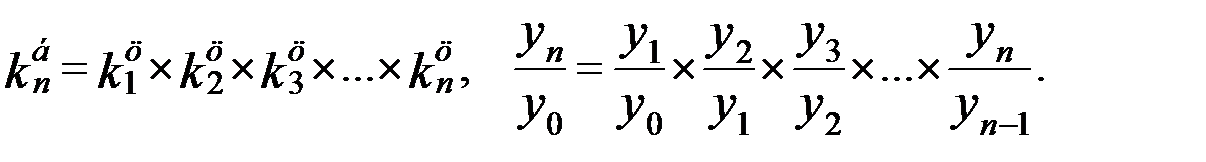
Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением одного процента прироста

,

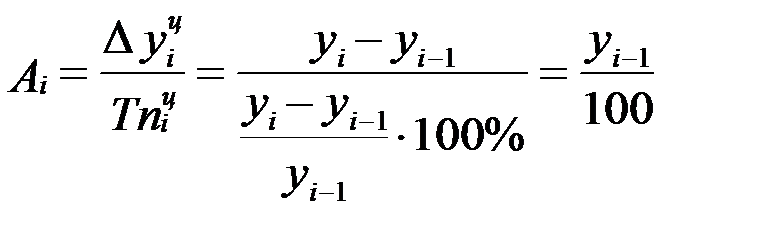т.е. этот показатель рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени.

Рассмотрим пример 2.1 расчета показателей ряда динамики. Имеются данные о количестве зарегистрированных безработных в одной из областей РФ (табл. 2.1.).

Таблица 2. 1

Расчет показателей ряда динамики

Годы
Количество зарегистрированных безработных (человек)
Абсолютный прирост базисный (чел.)	-
Абсолютный прирост цепной (чел.)	-				-2708	-10002
Коэффициент роста базисный	-	1,228	2,282	2,938	2,829	2,425	2,490
Коэффициент роста цепной	-	1,228	1,858	1,287	0,963	0,857	1,027
Темп роста базисный, %	-	122,8	228,2	293,8	282,9	242,5	249,0
Темп роста цепной, %	-	122,8	185,8	128,7	96,3	85,7	102,7
Темп прироста базисный, %	-	22,8	128,2	193,8	182,9	142,5	149,0
Темп прироста цепной, %	-	22,8	85,8	28,7	-3,7	-14,3	2,7
Абсолютное значение одного процента прироста, чел.	-

§ 2.3. Средние характеристики ряда динамики

Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Рассмотрим две категории этих показателей:

1) средние уровни ряда,

2) средние показатели изменения уровней ряда.

Метод расчета среднего уровня ряда динамики зависит от вида временного ряда.

Для интервального ряда динамики абсолютных показателей средний уровень за период определяется по формуле простой средней арифметической

,

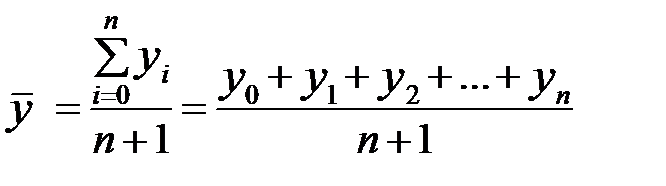где 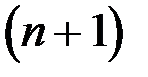- число уровней ряда (нумерация начата с нуля).

Средний уровень моментного динамического ряда определяется несколько иначе. Пусть промежутки времени между датами одинаковы. Предполагается непрерывное линейное изменение уровня в промежутках между двумя датами. Тогда расчет среднего уровня можно представить формулой (которую принято называть средней хронологической):

.

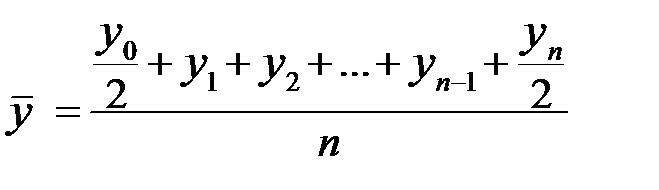Если промежутки времени между датами неодинаковы, то формула средней хронологической имеет вид:

,

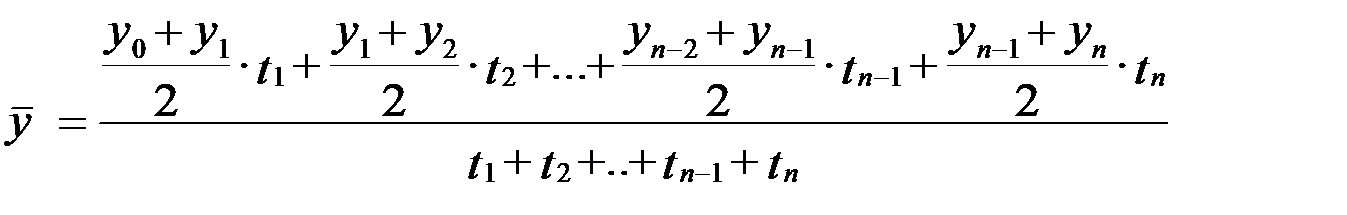где 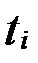- промежуток времени между уровням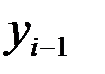и и .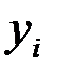

Если предположить, что в течение времени 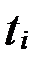уровень ряда 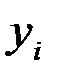остается неизменным, то средний уровень ряда рассчитывается по формуле средней арифметической взвешенной:

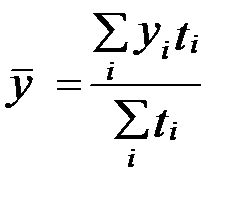
При определении средних уровней временного ряда нужно иметь в виду, что средняя будет достаточно надежной характеристикой ряда динамики, если она характеризует период с более или менее стабильными условиями развития.

Средний абсолютный прирост рассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:

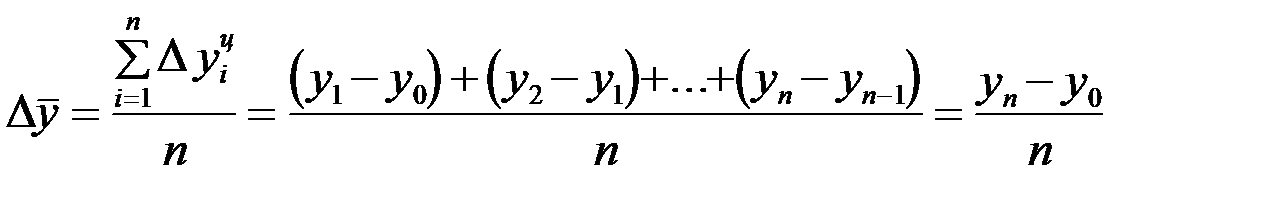
Напомним, что в принятых здесь обозначениях, число уровней ряда равно 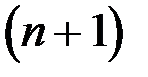, а число аналитических показателей равно .

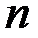Средний коэффициент роста вычисляется по формуле средней геометрической из коэффициентов роста за отдельные периоды:

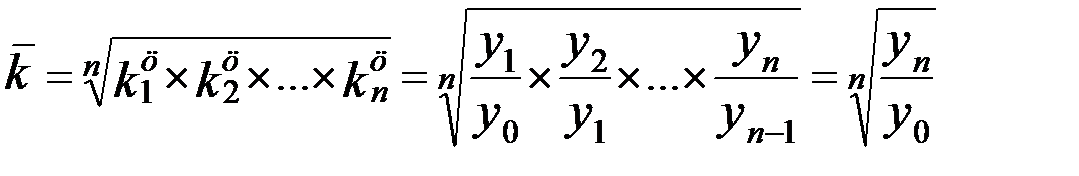
Средний коэффициент роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода изменялись уровни динамического ряда.

Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:

.

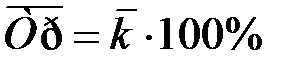Средний темп роста, рассчитанный по данным о конечном и начальном уровнях временного ряда, можно использовать только в случае более или менее равномерного изменения уровней.

§ 2.4. Выявление и характеристика основной тенденции развития (тренда)

Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени.

Уровни ряда динамики формируются под совокупным влиянием множества длительно и кратковременно действующих факторов и в том числе различного рода случайных обстоятельств. Выявление основной закономерности изменения уровней ряда предполагает ее количественное выражение, в некоторой мере свободное от случайных воздействий. Выявление основной тенденции развития (тренда) называется в статистике также выравниванием временного ряда, а методы выявления основной тенденции – методами выравнивания. Выравнивание позволяет характеризовать особенность изменения во времени данного динамического ряда в наиболее общем виде как функцию времени, предполагая, что через время можно выразить влияние всех основных факторов.

Один из наиболее простых приемов обнаружения общей тенденции развития явления – укрупнение интервала динамического ряда. Первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Например, ряд, содержащий данные о месячном выпуске продукции, может быть преобразован в ряд квартальных данных. Вновь образованный ряд может содержать либо абсолютные величины за укрупненные по продолжительности промежутки времени (эти величины получают путем простого суммирования уровней первоначального ряда абсолютных величин), либо средние величины. При этом отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается действие основных факторов изменения уровней (общая тенденция).

Выявление основной тенденции может быть осуществлено также методом скользящей средней. Для определения скользящей средней формируем укрупненные интервалы, состоящие из одинакового числа уровней 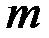. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня динамического ряда на один уровень. Тогда первый интервал будет включать уровни 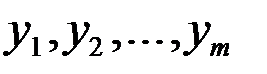; второй – уровни 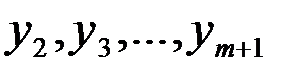и т.д. Интервал сглаживания «скользит» по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяем сумму значений уровней, на основе которых рассчитываем скользящие средние. Полученная средняя относится к середине укрупненного интервала. Поэтому технически удобнее укрупненный интервал составлять из нечетного числа уровней ряда. Нахождение скользящей средней по четному числу уровней создает неудобство, вызываемое тем, что средняя может быть отнесена только к середине между двумя датами. В этом случае необходима дополнительная процедура центрирования средних. При использовании приема скользящей средней сглаженный ряд сокращается по сравнению с исходным рядом на 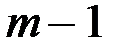уровней. Покажем порядок расчета скользящих средних.

Пример 2.2.

Имеются данные, характеризующие динамику производства продукции предприятия по месяцам (графы 1 и 2 табл. 2.2). Требуется произвести сглаживание ряда, применяя трехмесячную скользящую среднюю.

Решение.

Чтобы рассчитать первую скользящую среднюю, находим сумму валовой продукции за январь, февраль, март (графа 3) и делим ее на 3:

.

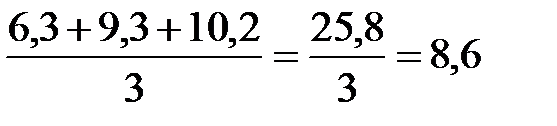Найденную среднюю относим к февралю (т.е. к среднему из трех суммируемых членов – графа 4). Для отыскания второй скользящей средней находим сумму валовой продукции за февраль, март, апрель и делим на 3:

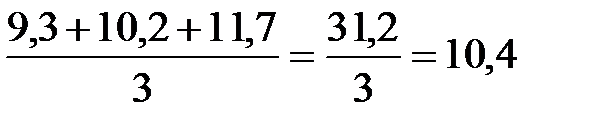
Найденную среднюю относим к марту и т.д.

Результаты подсчета скользящих сумм и средних показаны в графах 3 и 4 таблицы.

Таблица 2. 2

Расчет скользящих средних уровней ряда

Месяц	Объем продукции, млн. руб.	Скользящая сумма трех членов	Скользящая средняя
Январь	6,3	-	-
Февраль	9,3	25,8	8,6
Март	10,2	31,2	10,4
Апрель	11,7	34,5	11,5
Май	12,6	36,0	12,0
Июнь	11,7	38,3	12,8
Июль	14,0	38,3	12,8
Август	12,6	39,6	13,2
Сентябрь	13,0	39,9	13,3
Октябрь	14,3	40,8	13,6
Ноябрь	13,5	42,3	14,1
Декабрь	14,5	-	-

Для того чтобы представить количественную модель, выражающую общую тенденцию изменений уровней динамического, ряда во времени, используется аналитическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной кривой. Предполагается, что она отражает общую тенденцию изменения во времени изучаемого показателя.

При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени 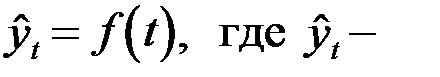уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени .

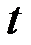Наиболее часто для аналитического выравнивания используются следующие виды трендовых моделей:

1. Линейная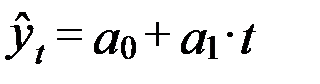
2. Парабола второго порядка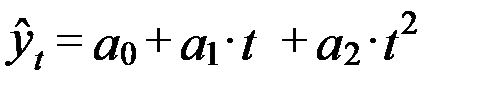
3. Парабола третьего порядка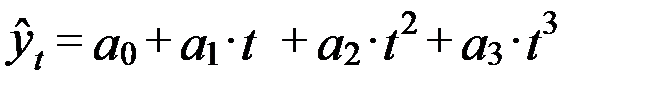
4. Показательная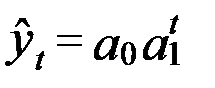
5. Гиперболическая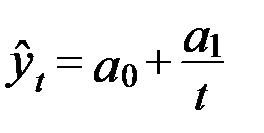
6. Логарифмическая парабола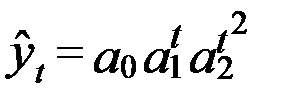
7. Логистическая кривая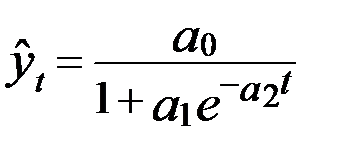
8. Кривая Гомперца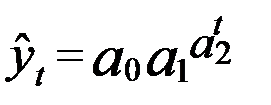

Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться также на результаты предыдущих исследований в данной области.

На практике для этих целей прибегают к анализу графического изображения уровней динамического ряда.

При выборе формы уравнения следует исходить и из объема имеющейся информации. Чем больше параметров содержит уравнение тренда, тем больше должно быть наблюдений при одной и той же степени надежности оценивания.

Выбор формы кривой может осуществляться на основе принятого критерия, в качестве которого может служить сумма квадратов отклонений фактических значений от значений, рассчитанных по уравнению тренда. Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия.

Рассмотрим аналитическое выравнивание ряда динамики по прямой, т.е. аналитическое уравнение вида:

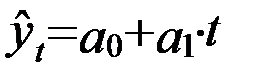
где 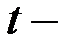порядковый номер периодов или моментов времени.

Параметры 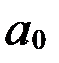и 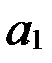прямой рассчитываются по методу наименьших квадратов (МНК). Система нормальных уравнений для нахождения параметров 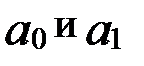в данном случае имеет вид:

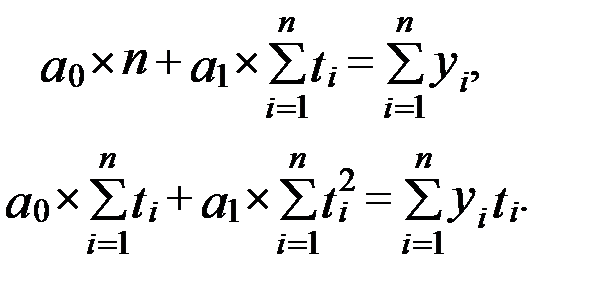
Поиск параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю. При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие ранее этого уровня, обозначаются натуральными числами со знаком минус (-1,-2,-3 и т.д.), а позже – натуральными числами со знаком плюс (+1, +2, +3 и т.д.)

Если число уровней динамического ряда четное, периоды времени верхней половины ряда (до середины) нумеруются -1,-3, -5 и т.д., а нижней-+1,+3,+5, и т.д. Возможна также нумерация с шагом единица:

… -3,5; -2,5; -1,5; -0,5; 0,5; 1,5; 2,5; 3,5; ….

Замечание. Иногда в случае четного числа уровней ряда их ошибочно нумеруют: …, -3, -2, -1, 1, 2, 3,…. При этом нарушают принцип равного шага, так как шаг между -1 и 1 равен 2, а остальные шаги равны единице.

При этом условии 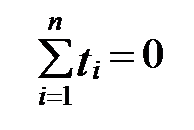и система нормальных уравнений преобразуется следующим образом:

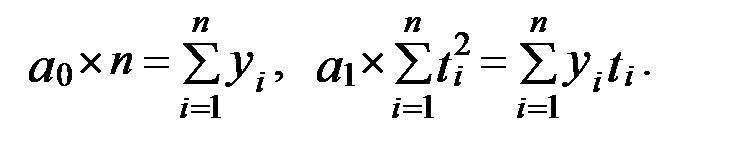
Тогда получим:

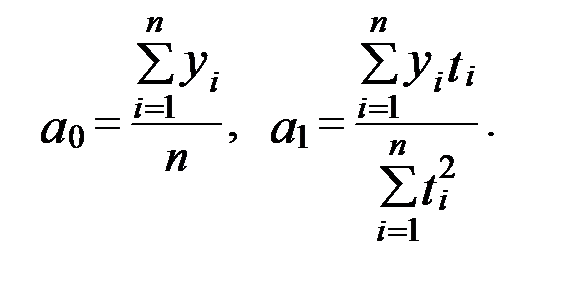
Пример 2. 3. Рассмотрим аналитическое выравнивание ряда динамики по линейной зависимости (табл. 2.3).

Используя итоги граф 2, 4 и 5, определим параметры уравнения прямой

.

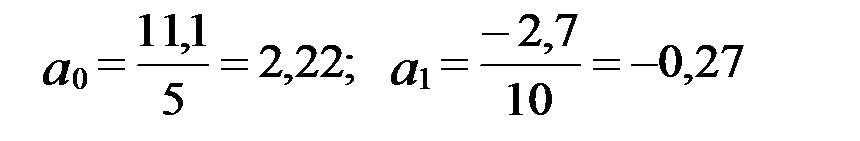Уравнение прямой ряда динамики: .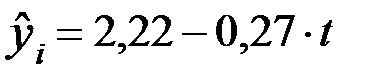

Таблица 2. 3

Строительство жилья

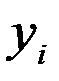
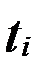
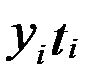
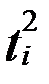
Годы	Построено, млн.кв.м.	Условное время			Выравненные уровни ряда
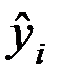
	2,9	-2	-5,8		2,76
	2,4	-1	-2,4		2,49
	2,1				2,22
	1,9		1,9		1,95
	1,8		3,6		1,68
Итого	11,1		-2,7		11,10

Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Возможность экстраполяции обеспечивается двумя обстоятельствами:

1) общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;

2) тенденция развития явления характеризуется тем или иным аналитическим уравнением. Экстраполируя при 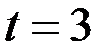, находим уровень 2005 года, равный 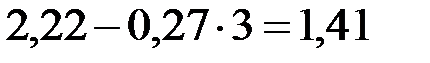млн.кв.м.

При составлении прогнозов оперируют не точечной, а интервальной оценкой, определяя так называемые доверительные интервалы прогноза. Величина доверительного интервала определяется по формуле

,

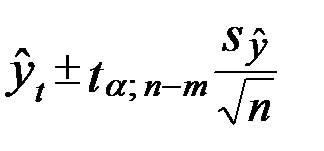где - среднее квадратическое отклонение от тренда;

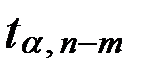- табличное (критическое) значение критерия Стьюдента при уровне значимости ;

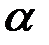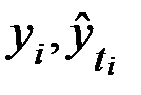- соответственно фактические и расчетные значения уровней динамического ряда;

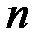- число уровней ряда;

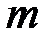- количество параметров в уравнении тренда (для уравнения прямой 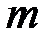= 2).

Критические значения критерия Стьюдента можно определить с помощью программы Microsoft Office Excel. Нажать , выбрать статистическую функцию СТЬЮДРАСПОБР. Задать вероятность равную уровню значимости (например, 0,05 или 0,01) и число степеней свободы .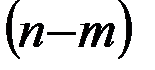

Используя данные, рассчитаем среднюю квадратическую ошибку линейного уравнения тренда: 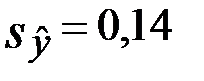млн.кв.м. Величина относительной ошибки составит:

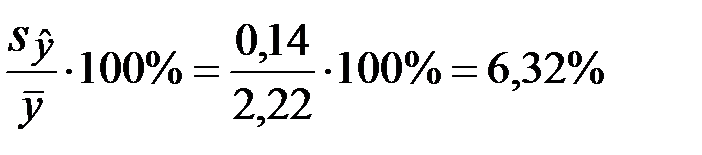
Следует помнить, что прием аналитического выравнивания содержит в себе ряд условностей, связанных, прежде всего, с тем, что уровни, характеризующие тот или иной динамический ряд, рассматриваются как функция времени. В действительности же развитие явлений обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие факторы влияли на развитие, в каком направлении, и с какой интенсивностью. Развитие явлений во времени выступает как внешнее выражение этих факторов, как их суммарное действие, оказывающее влияние на изменение уровня в отдельно взятые промежутки или моменты времени. Выявить основную тенденцию развития явления методом наименьших квадратов можно лишь тогда, когда выяснено, что изменяющиеся во времени процессы протекают на всем рассматриваемом промежутке времени одинаково, что их количественное и качественное изменение происходит под действием одного и того же комплекса основных факторов, определяющих движение данного ряда динамики. Экстраполяция на отдаленные даты подвержена более значительным ошибкам, чем краткосрочная экстраполяция.

§ 2.5. Понятие сезонной неравномерности и ее характеристика

Слагаясь под совместным воздействием систематических и случайных факторов, уровень ряда динамики испытывает также воздействие причин, обусловленных периодичностью колебаний.

В рядах внутригодичной динамики, можно выделить три важнейшие составляющие колеблемости уровней временного ряда: тренд, сезонную и случайную компоненты.

Таким образом, при анализе колеблемости динамических рядов наряду с выделением случайных колебаний возникает и задача изучения периодических («сезонных») колебаний.

В широком понимании, к сезонным, относят все явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодичных изменений, т.е. более или менее устойчиво повторяющиеся из года в год колебания уровней. К сезонным явлениям относят, например, потребление электроэнергии; неравномерность производственной деятельности в отраслях пищевой промышленности, связанных с переработкой сельскохозяйственного сырья; перевозки пассажирским транспортом.

Для исчисления индексов сезонности применяют методы, зависящие от характера общей тенденции ряда динамики. Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности вычисляют непосредственно по эмпирическим данным без их предварительного выравнивания. Для расчета индексов сезонности необходимо иметь помесячные данные минимум за три года.

Для каждого месяца рассчитывается средний за несколько лет уровень 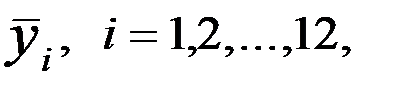затем рассчитывается среднемесячный уровень для всего анализируемого ряда 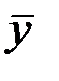(за все месяцы всех рассматриваемых лет). По этим данным определяются индексы сезонности как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда:

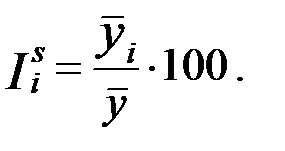
Пример 2. 4. Рассмотрим расчет индекса сезонности, если ряд не содержит явной тенденции.

Таблица 2. 4

Реализация картофеля на рынках города за три года, т:

Год

Месяц

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

Применяя формулу средней арифметической простой 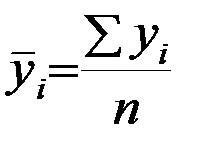, определим среднемесячные уровни за три года. Общее среднее значение равно 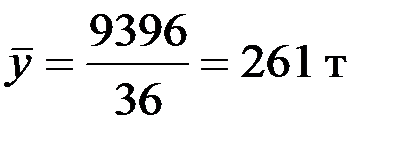. Индексы сезонности рассчитаем по формуле .

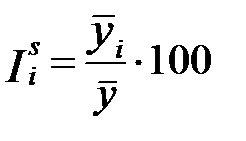Таблица 2. 5

Расчет индексов сезонности

Месяц	Сумма за три года, т	Среднемесячная 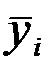за три года	Индексы 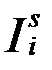сезонности, %
январь			26,3
февраль			27,6
март			28,7
апрель			96,9
май			129,1
июнь			178,5
июль			110,0
август			41,0
сентябрь			243,3
октябрь			201,0
ноябрь			69,7
декабрь			47,9
Итого		261	100,0

Индексы сезонности показывают, что наименьший спрос приходится на январь-февраль, а наибольший – на сентябрь-октябрь.

Ниже построен график сезонной волны реализации картофеля (рис. 2.1).

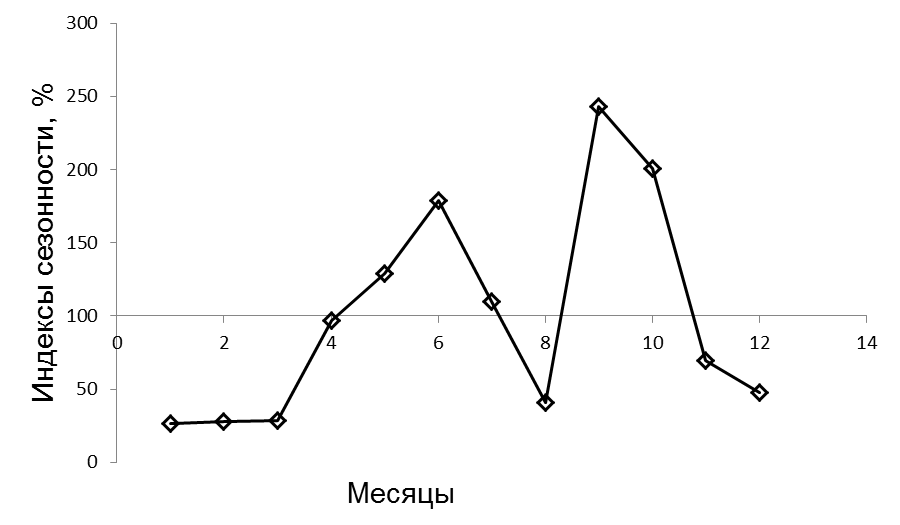
Рисунок 2. 1. Волна сезонности при отсутствии тренда

Когда уровни динамического ряда проявляют тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выравненными. Для расчета индексов сезонности в таких рядах динамики применяется формула

,

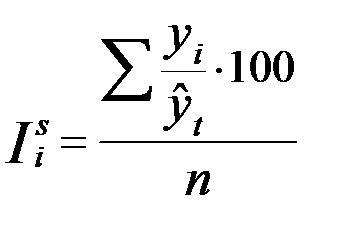где 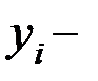фактические ряда;

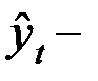уровни ряда, рассчитанные по уравнению тренда;

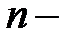число лет.

Пример 2. 5.

Рассмотрим расчет индексов сезонности при наличии тренда.

Таблица 2. 6

Динамике заготовок сельскохозяйственной продукции

области по кварталам за три года:

Квартал	Заготовлено продукции, тыс. руб.
Первый год	Второй год	Третий год
I
II
III
IV

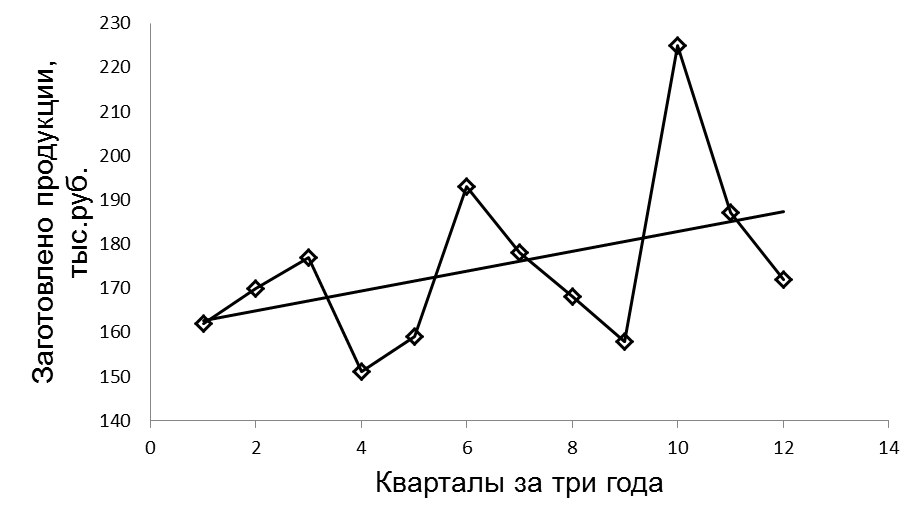
Рисунок 2. 2. Тренд и сезонные колебания

Из графика видна некоторая тенденция роста заготовок. Произведем выравнивание по линейной зависимости.

Определим значения 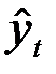по уравнению 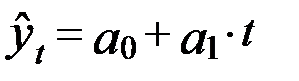. Параметры линейного уравнения рассчитаем по формулам:

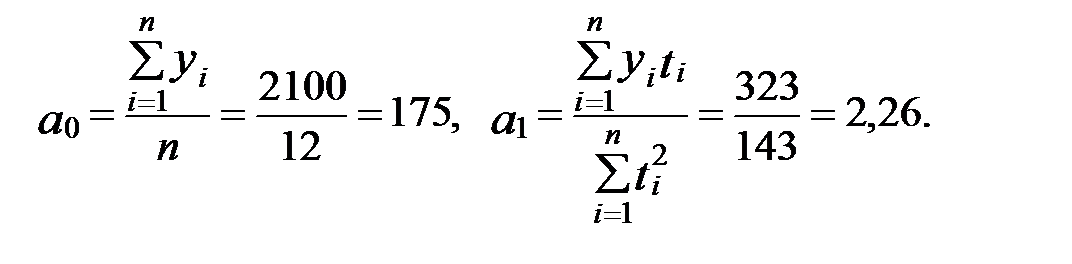
Следовательно, уравнение прямой имеет вид .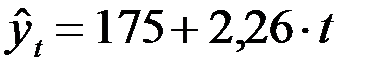

Подставив значения в уравнение прямой рассчитаем значения 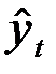(в предпоследнем столбце табл. 2.7). В последнем столбце табл. 6.7 для каждого квартала рассчитаны процентные отношения .

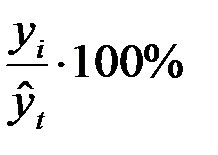Таблица 2. 7

Учет тренда при расчете индексов сезонности

Квартал	Фактические уровни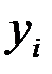
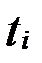
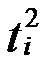
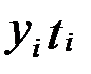
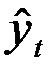
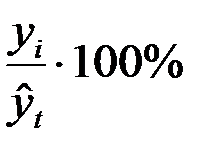
I		-5,5	30,25	-891,0	162,6	99,6
II		-4,5	20,35	-765,0	164,8	103,2
III		-3,5	12,25	-619,5	167,1	195,9
IV		-2,5	6,25	-377,5	169,4	89,1
I		-1,5	2,25	-238,5	171,6	92,7
II		-0,5	0,25	-96,5	173,9	111,0
III		0,5	0,25	89,0	176,1	101,1
IV		1,5	2,25	252,0	178,4	94,2
I		2,5	6,25	395,0	180,7	87,4
II		3,5	12,25	787,5	182,9	123,0
III		4,5	20,25	841,5	185,2	101,0
IV		5,5	30,25	946,0	187,3	91,8
Итого			143,0			-

Затем просуммируем полученные процентные отношения за три года по одноименным кварталам. Разделив поквартальные суммы на число лет, получим индексы сезонности.

Индексы сезонности характеризуют размеры заготовок сельскохозяйственной продукции в зависимости от времени года.

Таблица 2. 8

Расчет индексов сезонности при наличии тренда

Квартал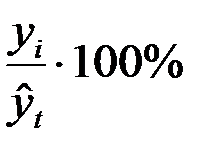
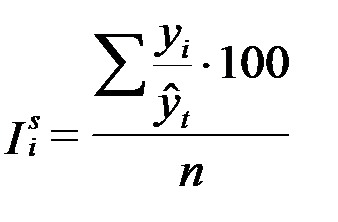
1-й год	2-ой год	3-ий год
I	99,6	92,7	87,4	93,2
II	103,2	111,0	123,0	112,4
III	105,9	101,1	101,0	102,7
IV	89,1	94,2	91,8	91,7

Наибольший удельный вес заготовок приходится на второй квартал.

Дата добавления: 2014-12-23