Верхняя и нижняя сумма Дарбу

Определенный интеграл и его геометрический смысл (задача о площади криволинейной трапеции). Приближенное вычисление определенных интегралов, формулы трапеций и Симпсона.

Пусть функция у = f (x) определена на отрезке [ а, b ]. Разобьем сегмент [ а, b ] произвольным образом на n частей точками .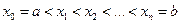

Обозначим через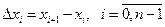

На каждом из сегментов 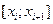выберем произвольные точки 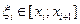и составим интегральную сумму:

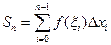Обозначим 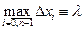. Если $ конечный 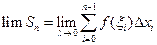, не зависящий от способа разбиения отрезка [ а, b ] и выбора точек 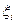, то его значение называется определенным интегралом от функции f (x), его обозначение 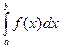, а функция f (x) называется интегрируемой на [ а, b ].

Т1. Если функция f(x) интегрируема на [а, b], то она ограничена (последовательность называется ограниченной, если $ M>0, что для 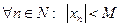) на этом сегменте. Если не ограничена => не интегрируема.

ДОК-ВО

Если функция f (x) не ограничена на [ а, b ], то $ по крайней мере одна точка с Î [ а, b ], в окрестности которой эта функция принимает сколь угодно большие по модулю значения. Тогда хотя бы один из отрезков [ x_i; x_{i +1}] ' c Þ за счет выбора точки 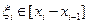произведение 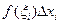можно сделать как угодно большими по модулю Þ 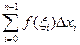может быть сделана как угодно большой, значит не существует конечного предела суммы Þ неограниченная функция не является интегрируемой. ЧТД.

Покажем, что не всякая ограниченная функция является интегрируемой:

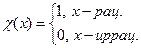
Функция ограничена, покажем, что она не интегрируема.

1) пусть 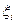– рац.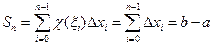

2) пусть 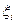– иррац.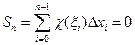

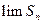зависит от выбора точек => функция не интегрируема.

Пусть функция у = f (x) ограничена на отрезке [ а, b ] и Þ ограничена на каждом из сегментов [ x_i; x_{i +1}], тогда $ m _i и M_i, где

ü 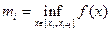– инфимум (точная нижняя грань: мн-во 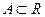наз-ся ограниченным снизу, если 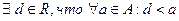(d-нижняя грань мн-ва А). Мн-во всех нижней граней обозначим ч/з D максим.из нижних граней наз-ся точной нижней гранью)

ü 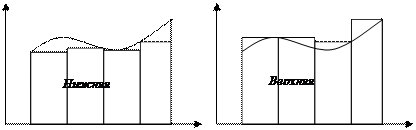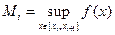– супремум (точная верхняя грань: мн-во 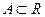наз-ся ограниченным сверху, если сущ-ет 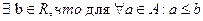(b-верхняя грань мн-ва А). Мн-во всех верхних граней обозначим ч/з А наим.из верхних граней наз-ся точной верхней гранью)

Верхняя сумма Дарбу: 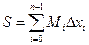Геометрический смысл верхней и нижней суммы Дарбу:

Нижняя сумма Дарбу: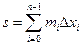

Т(необх. и дост. условие интегрируемости функции на [ а, b ] ). Для того чтобы ограниченная на [ а, b ] функция у = f (x) была интегрируема на этом отрезке Û для " e > 0 $ такое разбиение отрезка [ а, b ], что S – s < e.

Достаточные условия интегрируемости:

1) Если функция f (x) непрерывна на [ а, b ], то она интегрируема на нем.

2) Если функция f (x) монотонна на [ а, b ], то она интегрируема на нем.

3) Если функция f (x) ограничена на [ а, b ] и имеет лишь конечное число точек разрыва (т.е. является кусочно-непрерывной, разрывы I рода), то она интегрируема на [ а, b ].

Геометрический смысл (задача о площади криволинейной трапеции)

Пусть на отрезке [ а, b ] задана непрерывная положительная функция у = f (x).

Криволинейная трапеция – фигура, ограниченная сверху – графиком функции у = f (x), снизу – осью Ox, справа и слева – вертикальными прямыми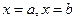

Разобьем отрезок [ а, b ] произвольным образом на n частей точками 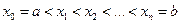и через каждую точку 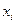проведем вертикальные прямые до пересечения с графиком функции у = f (x).

Обозначим через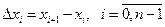

На каждом из сегментов 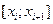выберем произвольные точки 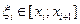и на 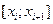построим прямоугольник высотой 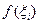, тогда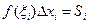

Составим интегральную сумму:

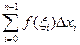= площади ступенчатого тела.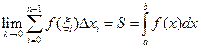

Формулы трапеций. Для приближенного вычисления 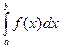, где функция f (x) непрерывна на [ а, b ], делят отрезок [ а, b ] на n равных частей и выбирают шаг вычислений 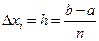. Пусть x_i – точки деления, x_i = a + ih, i = 0.. n.

Формула трапеций:

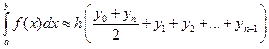
с абсолютной погрешностью

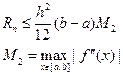
Для достижения заданной точности e шаг вычислений определяется из неравенства:

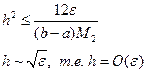
значения h округляется в сторону уменьшения так, чтобы n = (b – a) / h было целым. Установив h, вычисляют интеграл, беря значение подынтегральной суммы хотя бы с одним запасным десятичным знаком.

Формулы Симпсона (параболическая). При применении формулы Симпсона n должно быть четным. Берется [ x₀; x ₂] через три точки (x₀,y₀), (x₁,y₁), (x₂,y₂) проводят параболы и считают

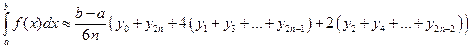
с абсолютной погрешностью

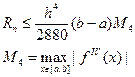
Шаг вычислений определяется из неравенства:

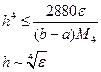h имеет порядок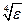

Значения h округляют в сторону уменьшения так, чтобы n = (b – a) / h было целым четным числом.

ЗАМЕЧАНИЕ: так как определение M ₂ и M ₄, вообще говоря, затруднительно, то на практике h подбирают исходя из здравого смысла, грубой прикидки. Затем шаг уменьшают вдвое и заново проводят вычисления. Если новый результат совпадает с полученным в сохраняемых нами десятичных знаках, то вычисления заканчиваются.

Для вычисления абсолютной погрешности формулы Симпсона можно применять принцип Рунге:

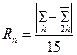
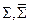– результаты вычисления по формуле Симпсона соответственно с шагом h и 2 h.

Не обязательно Свойства 1° если функции f (x) и j (x) интегрируемы на [ а, b ], то функция a f (x) + b j (x) также интегрируема на [ а, b ]: 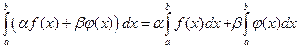2° будем считать по определению 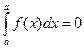3° если функция f (x) интегрируема на [ а, b ], то она интегрируема и на [ b, а ]: 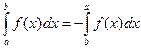4° если функция f (x) интегрируема на " двух из отрезков [ а, b ], [ а, c ], [ c, b ], то она интегрируема и на третьем отрезке: 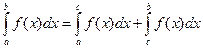5° если функция f (x) интегрируема на [ а, b ], то | f (x)| также интегрируема и на [ b, а ]. При этом: 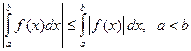Обратное утверждение неверно, т.е. из интегрируемости | f (x)| не следует интегрируемость f (x): 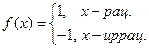| f (x)| = 1 интегрируема, но f (x) не интегрируема. 6° если функция f (x) интегрируема на [ а, b ] и f (x) > 0, то 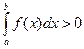7° [теорема о двусторонней оценке] если функция f (x) интегрируема на [ а, b ] и m £ f (x) £ M, то 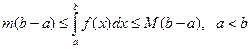8° [теорема о среднем] если функция f (x) непрерывна на [ а, b ], то $ точка c Î(а, b):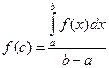

Дата добавления: 2015-01-03