Лемма Неймана-Пирсона

Л.: оптимальным критерием К* для проверки двух простых гипотез H₀: Ө=Ө₀, H₁: Ө=Ө₁, при заданном уровне значимости α является критерий К*, критическим множеством для которого является W^*:

W* = { 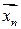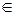χ_n│ },

где const C определяют исходя из условия:

С: P(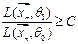) = α

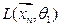, -значение функций правдоподобия.

С помощью этой леммы можно построить оптимальный критерий проверки двух простых гипотез. Статистическая гипотеза Н₀ основывается на принципе в соответствии с которым маловероятные события считаются невозможными, т.е., если выборка попадает в критическое множество с малой вероятностью, то естественно предположить, что утверждение, которое привело к этому маловероятному событию не соответствует истине и отклонить его.

За основную гипотезу естественно принять утверждение, отклонение которого, когда оно действительно является верным, приводит к более тяжелым последствиям, нежели его принятия при справедливости альтернативного. Основную гипотезу формулируем так, чтобы она противоречила данным, иначе нет смысла ее формулировать.

Общая схема проверки параметрических гипотез выглядит так: Н₀: Ө=Ө₀

1. сначала формулируют альтернативную гипотезу Н₁ исходя из условий задачи

2. задают уровень значимости α (по умолчанию 0,05)

3. определяется выборочное распределение статистики при условии, что гипотеза Н₀ является верной

4. по заданным уровню значимости α и объему выборки n определяется критическое множество критерия К в зависимости от вида альтернативной гипотезы

5. по выборке 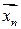=(x₁,x₂,…,x_n) вычисляют наблюдаемое значение статистики U_{наблюдаемое} =U()

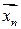6. делается статистическое решение: если U_{наблюдаемое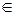} критическому множеству W, следовательно, выборка попадает в критическое множество(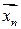 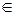W), то основная гипотеза отклоняется в пользу альтернативной. Делается вывод, что на заданном уровне значимости основная гипотеза неверна. Если выборка не принадлежит критическому множеству(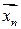 W), то говорят, что выборочные данные не противоречат основной гипотезе.

Критерий («Хи-квадрат»)

Одним из наиболее широко применяемых на практике является критерий согласия, применяемый для проверки гипотез о виде распределения генеральной совокупности, для проверки гипотез об однородности выборок, о независимости признаков и т.д. Критерий согласия с основной гипотезой Н₀ принято называть критерием, в которых необходимо проверить только согласие выборочных данных с выдвинутой гипотезой. В таких критериях часто не формулируется альтернатива, подразумевая под ней все остальное. При применении этого критерия для проверки гипотезы о виде распределения в качестве меры расхождения эмпирического и теоретического (предполагаемого) законов распределения используют статистику 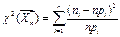, где n-объем выборки, r- число не пересекающихся множеств (для дискретных случайных величин) /интервалов (для непрерывных случайных величин) , на которые разбиты вся область возможных значений предполагаемой случайной величины, n_i-эмпирическая частота попадания в , p_i- вероятность того, что случайная величина попадет в множество (интервал) .

Закон распределения этой статистики при n (объем выборки)→∞ независимо от вида закона распределения случайной величины имеет теоретическое -распределение с числом степеней свободы k=r-l-1, где l- число параметров теоретического распределения, например, для нормального закона распределения N(a,σ) l=2, для экспоненциального Е(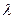) l=1. В целом для практики хватает n=

Общая схема проверки гипотезы Н₀: F(x, θ₁, θ₂, …)=F_T(x, θ₁, θ₂, …)

1. задается уровень значимости α;

2. по выборке 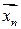находят значения оценок неизвестных параметров 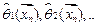используя для этого, как правило, оценки максимального правдоподобия

3. область возможных значений случайной величины Х разбивают на r непересекающихся множеств , подсчитывают их эмпирические частоты при этом

4. используя предполагаемый закон распределения Х подсчитывают вероятности . Если непрерывная случайная величина, то .

Замечание: критерий использует тот факт, что случайная величина имеет распределение близкое к стандартному нормальному N(0,1) .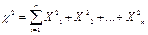

Чтобы это утверждение выполнялось достаточно, чтобы для всех множеств выполнялось условие 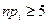для конечных объемов выборок. Если для некоторых не выполняется, то объединяем с соседними.

5. по заданным значениям α и n определяют критическое множество W критерия : )

6. по выборке 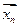вычисляют наблюдаемое значение статистики

7. принимается статистическое решение: если выборка , то основная гипотеза отклоняется, как не согласующаяся с данными выборки, в противном случае принимается и делается вывод, что данные не противоречат основной гипотезе.

Статистикой в мат. статистике называют любую функцию случайной выборки y(x₁,x₂,..,x_n).

15. Метод максимального правдоподобия. Точечное и доверительное оценивание параметров гауссовского распределения.

Дата добавления: 2015-01-03