
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон дисперсії поверхневого плазмон-поляритону
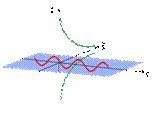
ППП є власною модою для межі розділу вакуум-ТТ (рис. 1):
|
| Рис. 1ППП на поверхні розділу двох ТТ |
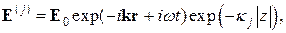 де
де 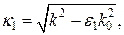
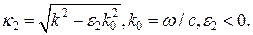
Для немагнітних систем рівняння Максвела можна звести до вигляду 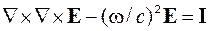 (де І – фугкція, що описує джерело). Якщо G — розв’язок цього рівняння з d-подібною правою частиною
(де І – фугкція, що описує джерело). Якщо G — розв’язок цього рівняння з d-подібною правою частиною 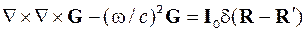 , то
, то 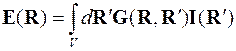 . Запишемо ел. поле через фотонний пропагатор (електродинам. функцію Гріна)
. Запишемо ел. поле через фотонний пропагатор (електродинам. функцію Гріна) 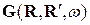 , що описує розповсюдженя фотона від точки джерела R’ до точки спостереження R:
, що описує розповсюдженя фотона від точки джерела R’ до точки спостереження R: 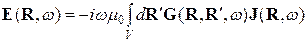 (1). Для двох напівпросторів зі пласкою межею розподілу він має вигляд
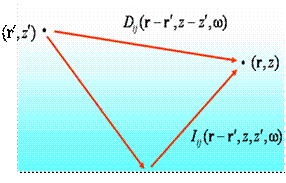
(1). Для двох напівпросторів зі пласкою межею розподілу він має вигляд 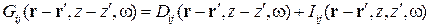 (див. Рис. 2).
(див. Рис. 2).
|
| Рис. 2 |
В площині хОу система однорідна, а вздовж осі Оz ні. Тому запишемо наявні функції в так званому k-z представленні, де вони розкладені в ряд Фур’є у площині хОу. Тоді матимемо
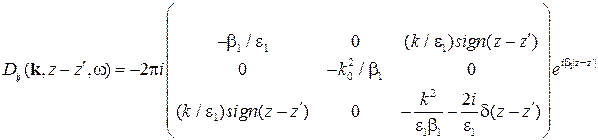 (2),
(2),
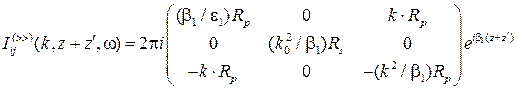 (3), де
(3), де 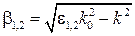 ,
,
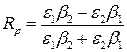 ,
, 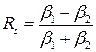 . Власними називають коливання, що можуть бути в системі за відсутності джерел. Для точкового джерела з (1) маємо
. Власними називають коливання, що можуть бути в системі за відсутності джерел. Для точкового джерела з (1) маємо 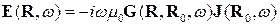 . Тоді умовою виникнення власних коливань є:
. Тоді умовою виникнення власних коливань є: 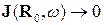 ,
, 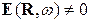 . Очевидно, це можливо лише за
. Очевидно, це можливо лише за 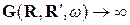 (4). Структура G визначається тензорами Dij та Iij. З (2) і (3) очевидно, що умова (4) може виконуватись лише якщо
(4). Структура G визначається тензорами Dij та Iij. З (2) і (3) очевидно, що умова (4) може виконуватись лише якщо 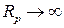 , або, що те саме,
, або, що те саме, 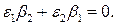 Підставляючи в останнє рівняння вирази у явному вигляді маємо дисперсійне рівняння
Підставляючи в останнє рівняння вирази у явному вигляді маємо дисперсійне рівняння 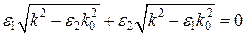 , де
, де 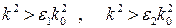 .
.
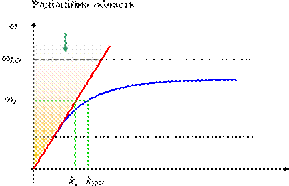
На рис. 3 показано дисперсійну залежність поверхневих хвиль (пряма показує розповсюдження світла у вакуумі).
|
Рис. 3 Закон дисперсії (залежність 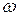 від від 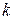 )для поверхневих хвиль
(крива)і е-м хвилі у вакумі (пряма) )для поверхневих хвиль
(крива)і е-м хвилі у вакумі (пряма)
|
Поверхневі нормальні моди безпосередньо не можуть взаємодіяти (а значить збуджуватись) з об'ємною електромагнітною хвилею, що розповсюджується у діелектричному середовищі або металі, оскільки їхні дисперсійні співвідношення зв'язують такі значенні частот та хвильових векторів радіаційних мод, де не виконується одночасно закони збереження енергії та імпульсу. Це добре видно на дисперсійній залежності: для збудження поверхневої хвилі із частотою 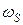 треба мати хвильовий вектор
треба мати хвильовий вектор 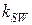 , а оптичний промінь має лише
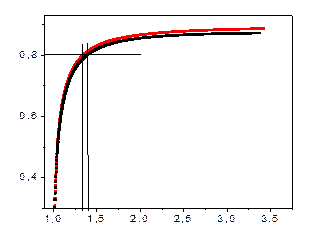
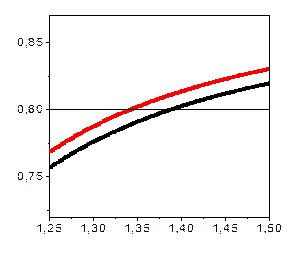
, а оптичний промінь має лише 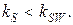 Тобто не існує такого кута падіння за якого електромагнітна хвиля зовнішнього випромінювання збуджувала б поверхневий плазмон-поляритон. При ПППР стан поверхні впливає на оптимальний кут збудження ППП, зсуваючи дисперсійну характеристику (рис. 4 і його збільшений варант рис. 5), а це в результаті веде до зсуву резонансної кривої (рис. 6)
Тобто не існує такого кута падіння за якого електромагнітна хвиля зовнішнього випромінювання збуджувала б поверхневий плазмон-поляритон. При ПППР стан поверхні впливає на оптимальний кут збудження ППП, зсуваючи дисперсійну характеристику (рис. 4 і його збільшений варант рис. 5), а це в результаті веде до зсуву резонансної кривої (рис. 6)
|
| Рис. 4 |
|
| Рис. 5 |
|
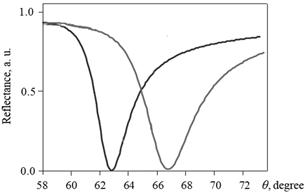
| Рис. 6 |
 41.Параметри, що впливають на збудження та розповсюдження ППП.
41.Параметри, що впливають на збудження та розповсюдження ППП.
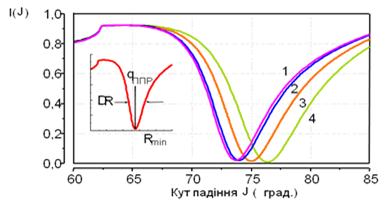
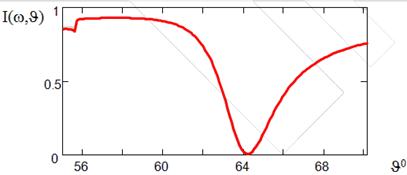
Крива ПППР має наступний вигляд де зображено графік інтенсивності відбитого світла. Мінімуму відповідає кут максимально ефективного збудження ПППР. Невеликий провал зліва має місце через те, що в дисперсійній залежності 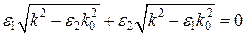 підкореневі вирази змінюють знак. Наступний рисунок демонструє зсув резонансної кривої при зміні товщини шару білка на досліджуваній поверхні (див. пункт іі з питання Методи збудження і реєстрації поверхневих хвиль) (кривим відпов. товщини 0, 1, 5 і 10 нм).
підкореневі вирази змінюють знак. Наступний рисунок демонструє зсув резонансної кривої при зміні товщини шару білка на досліджуваній поверхні (див. пункт іі з питання Методи збудження і реєстрації поверхневих хвиль) (кривим відпов. товщини 0, 1, 5 і 10 нм).
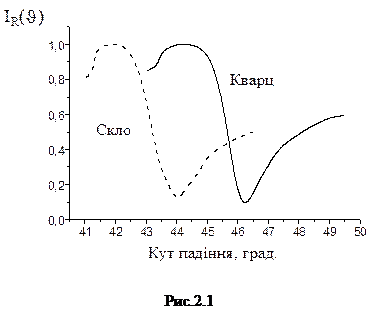 Таким чином, наявність дефектів на поверхні (у випадку, що розглядається такими дефектами виступають молекули білків) призводить до зсуву мінімуму резонансної кривої у бік більших кутів. Розглядаючи фактори, що можуть впливати на чутливість і точність вимірювання концентрації молекул у розчині (або концентрації тестованих молекул у біологічних рідинах – наприклад – крові) можна виділити такі їхні групи: -плівка де формується поверхнева хвиля; - поверхневий молекулярний шар; - математичні методи обробки результатів вимірювання спектрів відбиття. Насправді, розв'язки коректно сформульованих проблем можуть істотно поліпшити чутливість, селективність та точність вимірювання ППР при адсорбції на робочу поверхню шару біологічних молекул. Зауважимо, що особливістю метода ПППР є детектування зміни ефективного коефіцієнта заломлення Dn в шарі товщиною d, що відбувається на металічній поверхні перетворювача в результаті адсорбції молекул на поверхню, або в результаті протікання на цій поверхні реакції молекулярної взаємодії. Така зміна фізичних параметрів середовища, що досліджується, призводить до зсуву мінімуму кривої ППР який відповідає геометричним умовам найбільш повного перетворення енергії падаючого випромінення в поверхневий плазмон-поляритонний стан – класичний приклад резонансного поглинання. Ефективність ППР сенсора може бути охарактеризованою константою перетворення
Таким чином, наявність дефектів на поверхні (у випадку, що розглядається такими дефектами виступають молекули білків) призводить до зсуву мінімуму резонансної кривої у бік більших кутів. Розглядаючи фактори, що можуть впливати на чутливість і точність вимірювання концентрації молекул у розчині (або концентрації тестованих молекул у біологічних рідинах – наприклад – крові) можна виділити такі їхні групи: -плівка де формується поверхнева хвиля; - поверхневий молекулярний шар; - математичні методи обробки результатів вимірювання спектрів відбиття. Насправді, розв'язки коректно сформульованих проблем можуть істотно поліпшити чутливість, селективність та точність вимірювання ППР при адсорбції на робочу поверхню шару біологічних молекул. Зауважимо, що особливістю метода ПППР є детектування зміни ефективного коефіцієнта заломлення Dn в шарі товщиною d, що відбувається на металічній поверхні перетворювача в результаті адсорбції молекул на поверхню, або в результаті протікання на цій поверхні реакції молекулярної взаємодії. Така зміна фізичних параметрів середовища, що досліджується, призводить до зсуву мінімуму кривої ППР який відповідає геометричним умовам найбільш повного перетворення енергії падаючого випромінення в поверхневий плазмон-поляритонний стан – класичний приклад резонансного поглинання. Ефективність ППР сенсора може бути охарактеризованою константою перетворення 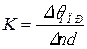 (1.3) що визначається ступенем перетворення інформації про процес біохімічної взаємодії, що відбувається на поверхні (зміна Dn) у відповідний вихідний сигнал приладу (зсув кута ППР DqППР). Зрозуміло, що чим ефективніше будуть відбуватись процеси збудження ППП, тим з більшою точністю можна реєструвати зміни характеристик резонансної системи при введенні на робочу поверхню тестованих молекул. Очевидно, що факторами, що зменшують ефективність збудження ППП є неідеальність поверхні, характеристики підкладинки на яку нанесено металічну плівку, та наявність уявної частини діелектричної функції при заданій частоті. На ці фактори можуть впливати такі технологічні процеси, як відпалювання золотої плівки, можливість застосування перехідних шарів та пасивування поверхні. На Рис.2.1 показані криві ППР для плівок золота з підшаром хрому, що нанесені при температурі 200С на скляну та кварцову підкладинку. Звідси видно, що зменшення коефіцієнту заломлення підкладинки призводить не тільки до зсуву кривої ППР у бік більших кутів, а також до ефективного зменшення напівширини кривої, що автоматично призводить до більш точного визначення положення її мінімуму.
(1.3) що визначається ступенем перетворення інформації про процес біохімічної взаємодії, що відбувається на поверхні (зміна Dn) у відповідний вихідний сигнал приладу (зсув кута ППР DqППР). Зрозуміло, що чим ефективніше будуть відбуватись процеси збудження ППП, тим з більшою точністю можна реєструвати зміни характеристик резонансної системи при введенні на робочу поверхню тестованих молекул. Очевидно, що факторами, що зменшують ефективність збудження ППП є неідеальність поверхні, характеристики підкладинки на яку нанесено металічну плівку, та наявність уявної частини діелектричної функції при заданій частоті. На ці фактори можуть впливати такі технологічні процеси, як відпалювання золотої плівки, можливість застосування перехідних шарів та пасивування поверхні. На Рис.2.1 показані криві ППР для плівок золота з підшаром хрому, що нанесені при температурі 200С на скляну та кварцову підкладинку. Звідси видно, що зменшення коефіцієнту заломлення підкладинки призводить не тільки до зсуву кривої ППР у бік більших кутів, а також до ефективного зменшення напівширини кривої, що автоматично призводить до більш точного визначення положення її мінімуму.

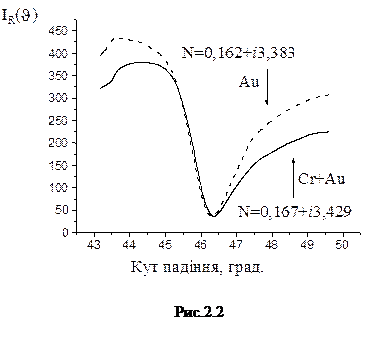 Іншим суттєвим фактором є проблема адгезії (прилипання) золотої плівки на кварцову підкладинку. Для збільшення адгезії використовують адгезійний шар хрому на який вже наносить ся плівка золота. Але оскільки шари хрому і золота дуже тонкі, таку систему Cr+Au можна розглядати як деяку плівку з ефективним комплексним коефіцієнтом заломлення. При цьому застосування адгезійного шару хрому призводить до невеликого розширення кривої ППР. Але зсуву мінімуму кривої при цьому майже не відбувається (див. Рис.2.2). Зауважимо, що збільшення уявної частини ефективного коефіцієнта заломлення призводить до збільшення коефіцієнта екстинкції, що погіршує ефективність перетворення (коефіцієнтом екстинкції називають величину що дорівнює сумі коефіцієнтів поглинання (відношення потоку випромінювання, що поглинуте тілом до потоку випромінювання, що падає на об'ємний зразок) та розсіяння (відношення потоку випромінювання, що розсіяне тілом до потоку випромінювання, що падає на дане тіло) середовища. Зрозуміло, що коефіцієнт екстинкції тим більший, чим більше значення уявної частини коефіцієнта заломлення).
Іншим суттєвим фактором є проблема адгезії (прилипання) золотої плівки на кварцову підкладинку. Для збільшення адгезії використовують адгезійний шар хрому на який вже наносить ся плівка золота. Але оскільки шари хрому і золота дуже тонкі, таку систему Cr+Au можна розглядати як деяку плівку з ефективним комплексним коефіцієнтом заломлення. При цьому застосування адгезійного шару хрому призводить до невеликого розширення кривої ППР. Але зсуву мінімуму кривої при цьому майже не відбувається (див. Рис.2.2). Зауважимо, що збільшення уявної частини ефективного коефіцієнта заломлення призводить до збільшення коефіцієнта екстинкції, що погіршує ефективність перетворення (коефіцієнтом екстинкції називають величину що дорівнює сумі коефіцієнтів поглинання (відношення потоку випромінювання, що поглинуте тілом до потоку випромінювання, що падає на об'ємний зразок) та розсіяння (відношення потоку випромінювання, що розсіяне тілом до потоку випромінювання, що падає на дане тіло) середовища. Зрозуміло, що коефіцієнт екстинкції тим більший, чим більше значення уявної частини коефіцієнта заломлення).
Чисельні моделювання і розрахунки показують, що зміна абсолютного значення коефіцієнта заломлення металічного покриття практично не впливає на величину константи перетворення К. Разом з тим зміни коефіцієнта екстинкції призводять до експоненціальної залежності зсуву резо-нансного кута DqППР як це показано на Рис.2.3. Тобто, для збільшення чутливості метода необхідно застосовувати такі технологічні процедури, що призводили б до зменшення коефіцієнта екстинкції металічної плівки.
Таким чином технологічні обробки металічної плівки можуть призводити до збільшення коефіцієнту перетворення, що дає покращення чутливості датчика ППР. Також див. останній абзац пит. Закон дисперсії поверхневого плазмон-поляритону (рисунки зміни дисперсійної кривої).
|
|
Дата добавления: 2015-01-03; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!