Решение задач 25—33 из учебника

Задача 25. При решении данной задачи ребятам предстоит освоить правила новой игры — игры «ползунок». Поэтому, проходя по классу, постарайтесь проконтролировать соблюдение всеми игроками правил игры, при необходимости возвращайте ребят к листу определений. Возможно, стоит в первых партиях турнира в каждой группе назначить контролёра (или двух), которые будут следить за соблюдением правил игры. Другой вариант — сыграть на доске несколько тренировочных партий.

Если вам приходилось играть в игру «ползунок» на поле 3 × 3, то вы, скорее всего, заметили, что Второй выигрывает здесь гораздо чаще, чем Первый. На самом деле Второй в этой игре имеет выигрышную стратегию: следуя определённым правилам, он может выиграть всегда, как бы ни играл Первый (мы ещё много будем говорить о выигрышных стратегиях в дальнейшем, в том числе и в игре «ползунок» на поле 3 × 3). Если вы хотите, чтобы члены группы были в равном положении, предложите ребятам перед началом каждой партии кидать жребий, кто будет Первым (с помощью кубиков, спичек или игры «камень—ножницы—бумага», например). Поскольку в игре «ползунок» ничьих не бывает, заполнять турнирную таблицу будет немного легче, чем для игры «крестики-нолики», и победителя будет легко определить, даже если у двух игроков наберётся одинаковое число очков. Если же число очков будет одинаковым сразу у троих игроков (в группе из трёх человек или у троих из четверых), то для определения победителя придётся проводить дополнительные партии.

Задача 26. Для решения задачи от учащихся требуется лишь понимание правил игры «ползунок». Напомните ребятам, что нужно каждый новый отрезок проводить красным или зелёным карандашом в зависимости от того, кто делает ход. Необходимые поля ребята найдут на вкладыше.

Очень важно, чтобы решение задачи закончилось проверкой. Главное условие — последняя позиция в цепочке действительно должна быть заключительной. Для этого на поле должна получиться ломаная, которую уже нельзя продолжить. Также нужно проверить, чтобы при переходе от каждой позиции к следующей добавлялся ровно один отрезок. Наконец, стоит просмотреть всю цепочку, проверяя, соответствует ли очерёдность хода цвету появившегося отрезка и соответствует ли следующая позиция предыдущей (все отрезки предыдущей позиции должны повториться и на следующей и сохранить цвет).

Задача 27. Здесь предстоит построить цепочку позиций игры «ползунок» с заданной заключительной позицией. Как и при решении задачи 7, учащийся может двигаться от начала к концу, следя за тем, чтобы на поле на каждом ходе появлялся только такой отрезок, который есть в заключительной позиции (учитывая и цвет), или от конца к началу, убирая по одному отрезку с одного из концов ломаной. В обоих случаях учащийся должен следить за очерёдностью хода, чтобы при каждом переходе от одной позиции к другой появлялся (или исчезал) отрезок соответствующего цвета. Несмотря на внешнюю похожесть этой задачи и задачи 7, данная задача оказывается существенно сложнее — это связано со спецификой игры «ползунок». В отличие от игры «крестики-нолики», где значки, которые игроки ставят на поле, никак не должны быть связаны между собой, в игре «ползунок» каждый следующий отрезок должен присоединяться к уже нарисованной ломаной. Учитывая, что отрезок должен быть ещё и определённого цвета, мы приходим к тому, что в данной задаче в качестве первого хода Первого нельзя брать любой из красных отрезков в заключительной позиции. В противном случае мы сталкиваемся с тем, что цепочку игры в некоторый момент нельзя продолжить и привести к заключительной позиции. Перебирая все возможные первые ходы Первого (красные отрезки в заключительной позиции) и пытаясь строить с каждым из них цепочку партии игры, мы приходим к выводу, что цепочку V позволяет построить лишь один из них — вертикальный верхний. Далее вплоть до шестой позиции вариантов при выборе следующего хода ни у Второго, ни у Первого нет. Таким образом, в данной задаче (в отличие от задачи 7) существуют лишь две подходящие цепочки V (см. ответ ниже).

Описанные выше особенности игры «ползунок» объясняют то, что данную задачу проще решать с конца, отбрасывая постепенно отрезки соответствующих цветов, ведь вариантов при выборе отрезка, который можно отбросить, существенно меньше (собственно один или два варианта).

Здесь мы уже не напоминаем учащемуся в условии о необходимости проверки, но это не значит, что она не нужна. Например, можно провести парную проверку, попросив ребят поменяться тетрадями. Полезно при этом предварительно спросить ребят, на что именно нужно обратить внимание при проверке.

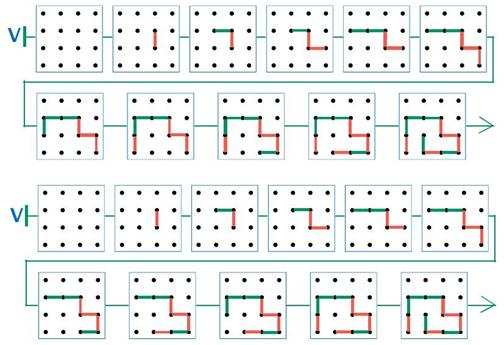
Ответ: два возможных варианта цепочки V:

Задача 28. Необязательная. Наиболее естественный путь решения этой задачи — экспериментальный. Надо предложить детям рисовать на черновике (например, на таком же поле на листе вырезания) несколько вариантов партий с заданным началом. Учащиеся, по сути дела, будут пользоваться методом случайного перебора вариантов. В этих попытках партии иногда будут заканчиваться ещё до одиннадцатого хода, в отдельных случаях одиннадцатый ход может быть не последним — ведь останутся возможные ходы. В ходе таких экспериментов дети могут понять закономерности игры и требуемый ход будет найден. Учителю здесь, как обычно, отводится роль консультанта, проверяющего точность следования правилам игры «ползунок».

Для того чтобы быстро проверить решение или подтолкнуть затрудняющегося в решении ученика, помогут некоторые математические (точнее, геометрические) соображения. Понятно, что если отвлечься от раскрашивания отрезков в красный и зелёный цвета, то задача будет сведена к тому, чтобы дополнить имеющиеся 3 звена (из четвёртой позиции цепочки) до ломаной из 11 звеньев, которую уже нельзя продолжить. Ломаная линия из 11 звеньев проходит через 12 точек (потому что сама себя она не пересекает). Это значит, что на нашем поле она не пройдёт через 4 точки из 16 точек поля. Таким образом, задача сводится к тому, чтобы построить ломаную, которую нельзя дальше продолжить, которая включает заданный отрезок из 3 звеньев и не проходит через какие-либо 4 точки поля. Можно сделать это по-разному, например так:

Такие рассуждения дают нам не только решение задачи, но и подход к более широкому кругу вопросов, возникающих вокруг данной задачи. Например, возможна ли вообще такая партия игры «ползунок» на поле 4 × 4, в которой выигрывает Второй? Да, если мы сможем построить ломаную из чётного числа звеньев. Сколько ходов вообще может быть в игре на поле 4 × 4? Например, может ли быть 20 ходов? Нет, так как точек на поле всего 16, а значит, ломаная может состоять не более чем из 15 ходов-звеньев.

Вы можете обсуждать вышеперечисленные вопросы, а можете совсем их не касаться. Однако приведённые рассуждения могут вам помочь в тот момент, когда у ребёнка работа над задачей застопорится. Если вам хотелось бы не подсказывать ему решение, а лишь навести на мысль, то достаточно замечаний типа: «Ты захватил в ползунок слишком много точек поля, поэтому ходов получилось больше, чем требуется. Попробуй оставить в стороне какие-то точки». Или что-то в этом роде в зависимости от ситуации.

Решений в данной задаче достаточно много. Поучительно сравнить решения, полученные разными ребятами, и выделить в них общее.

Ответ: одна из возможных цепочек:

Задача 29. Возможных партий игры «камешки» по таким правилам не так уж и много, всего 6. В двух из них выигрывает Второй:

5 — 4 — 0 и 5 — 1 — 0.

В остальных выигрывает Первый:

5 — 4 — 1 — 0; 5 — 4 — 3 — 0; 5 — 4 — 3 — 2 — 1 — 0; 5 — 2 — 1 — 0.

Для начала можно составить любую партию по таким правилам, затем определить в ней победителя и записать её в соответствующее окно. Однако в отличие от подобной задачи 13 такую партию не всегда можно легко переделать так, чтобы изменился победитель, поэтому подумать ребятам всё-таки придётся. Один из вариантов решения — игровой: поиграть с соседом в подобную игру и экспериментальным путём составить партии. Этот вариант также хорош для ребят, любящих составлять честные партии, в которых игроки не поддаются друг другу.

Другой вариант решения — метод перебора. Лучше всего начать такой перебор по первому ходу Первого и закончить его, как только найдутся две подходящие партии. Проще исследовать партии, где Первый берёт сразу несколько камешков, например 4. Тогда на втором ходу выигрывает Второй, цепочку получившейся партии можно записать во второе окно. Если Первый берёт на первом ходу 3 камешка, то дальше игра также идёт без вариантов и выигрывает Первый.

Задача 30. Сложность этой задачи в том, что ребятам необходимо учесть одновременно два условия: выиграть должен Первый и произойти это должно именно на седьмом ходу, поскольку длина цепочки задана. Хорошо, если ребята уже видят связи между длиной цепочки, числом ходов, сделанных в партии, и выигрышем определённого игрока. Действительно, в цепочке 8 позиций, значит, сделано 7 ходов, из них 4 крестика и 3 нолика. На последнем ходу, конечно, поставлен крестик. Как и в некоторых других задачах, здесь можно двигаться как от начала цепочки к концу, так и наоборот. Двигаясь с конца, ребята просто расставляют 4 крестика и 3 нолика в заключительной позиции, так чтобы было 3 крестика в ряд и не было других рядов из трёх одинаковых значков (ни крестиков, ни ноликов), а затем убирают по одному значку в соответствии с очерёдностью хода, начиная с одного из трёх крестиков, стоящих в ряд (3 крестика подряд должны появиться только на последнем ходу). Двигаться от начала здесь несколько сложнее, ведь придётся постоянно следить, чтобы игра не закончилась раньше или позже. Сложность подобной ситуации компенсируется лишь тем, что здесь Второй может подыгрывать Первому: поддаваться или просто плохо играть, не замечая своих выгодных ходов. Естественно, ребятам, которые хотят во что бы то ни стало построить честную партию (в которой оба игрока стремятся выиграть), мешать не надо, но им будет несколько сложнее.

Задача 31. Необязательная. В курсе 2 класса таких задач было довольно много. В курсе 3 класса задача на поиск русского слова с таким же мешком букв встречается впервые, поэтому напомним особенности подобных задач. Эти задачи отчасти из курса информатики и отчасти из курса русского языка. При этом формальное информатическое (или математическое) решение, состоящее в полном переборе всех слов, имеющих такой мешок букв, детям осуществить будет довольно сложно. Так, из 5 разных букв (как в слове ОТСЕВ, например) можно составить 120 разных цепочек букв. Поэтому, решая такие задачи, дети всё-таки больше угадывают слова, чем по-настоящему перебирают. При этом они интуитивно используют некоторые лингвистические соображения: например, какие сочетания букв более популярны в языке, а какие, наоборот, можно сразу отбрасывать. Поэтому вы, скорее всего, столкнётесь с тем, что кто-то из детей довольно легко решает такие задачи. Это как раз те дети, у которых языковая интуиция развита хорошо. А некоторым такие задачи будут даваться с трудом, при этом помочь им, не подсказав нужного слова, будет довольно затруднительно. Один из вариантов — предложить полный перебор, но подсказав первую букву искомого слова (тогда перебор существенно уменьшится). Другой вариант работы с подобной задачей — предложить подумать над ней дома или оставить её на будущее. В любом случае такие задачи лучше предлагать по желанию, вполне допустимо, если ребёнок решит её частично (для каких-то слов).

Ответ:

ОТСЕВ — СОВЕТ

ТЯПКА — ПЯТКА

АДРЕС — СРЕДА

СМОЛА — МАСЛО

Задача 32. Здесь ребята вспоминают особенности работы с конструкцией повторения. Если кто-то запутался, посоветуйте ему отмечать, сколько раз выполнены внутренние команды каждой конструкции повторения, ставя пометку около соответствующей конструкции, каждый раз доходя до слова КОНЕЦ. Также можно попросить в этой задаче ставить пометку на поле после выполнения каждой конструкции повторения целиком. Тогда в случае ошибки ребёнок (и вы) сможете понять, при выполнении какой части программы ошибка допущена. При правильном решении положение Робика на поле после выполнения программы совпадает с положением в начальной позиции.

Ответ: позиция Робика после выполнения программы Ю:

Задача 33. Необязательная. Задача имеет много разных решений, но именно от этого многообразия ребёнок и может растеряться. Первый вопрос: с какого условия начать? Наиболее конкретную информацию даёт последнее утверждение, ставим пятой бусиной вопросительный знак. Теперь поищем другие утверждения, связанные с вопросительным знаком, их два: третье и предпоследнее. Ставим точку в любое окно, идущее раньше вопросительного знака, а тире в любое окно, идущее позже. У нас есть утверждение, связанное с точкой, читаем его и ставим закрывающуюся скобку позже точки. Куда бы мы до этого ни поставили точку, место для закрывающейся скобки можно найти всегда. Оставшиеся утверждения никак не связаны с уже поставленными знаками, они не задают конкретных мест для оставшихся знаков, а говорят лишь о порядке между ними. Эти утверждения указывают на то, что двоеточие идёт из оставшихся знаков позже всех, поэтому ставим его в последнем свободном окне, три оставшихся знака расставляем как угодно.

Урок «Игра «сим»

Эта игра, хотя и использует в качестве поля игры окружность, лишь в малой степени является геометрической (в отличие, например, от игры «ползунок»). «Сим» — это игра, скорее, комбинаторная. Математики и другие профессионалы, использующие математический аппарат, имеют определённое представление о том, когда та или иная задача или метод её решения являются геометрическими, алгебраическими, аналитическими, комбинаторными, вероятностными и т. д. В последнее время в математике часто говорят о нелинейных задачах. Вырисовывается некоторый класс алгоритмических, информатических задач. Хотя эти различия и не входят в школьный курс, но они могут оказаться вам полезными при анализе стиля, в котором дети пытаются решать задачи, и почему задачи одного типа получаются у одних детей, а другого типа — у других.

В отличие, например, от игры «крестики-нолики», игра «сим» может для большинства оказаться незнакомой. Кроме того, по сравнению со всеми предыдущими играми здесь сложнее определить заключительную позицию, особенно если одноцветный треугольник в ходе игры так и не возник. Действительно, в игре «камешки» заключительная позиция видна всегда, в игре «крестики-нолики» отсутствие ряда из трёх одинаковых значков и наличие свободных клеток говорят о возможности продолжения игры. О том же в игре «ползунок» говорит наличие свободных точек, с которыми может быть соединён хотя бы один из концов ползунка. В игре «сим», если точек на окружности больше четырёх, дети могут не заметить того, что какие-то точки ещё не соединены, и закончить игру преждевременно. Обратите на это внимание учеников. Обсудите с ними, сколько всего отрезков может выходить из одной точки (на один меньше, чем всего точек). Таким образом, простой проверкой того, остались ли ещё возможные ходы, является пересчёт отрезков, выходящих из каждой точки (пересчитать их несложно).

Дата добавления: 2015-01-03