Степенные средние. Методика их расчета

К Степенным средним относятся:

1. средняя арифметическая

2. средняя гармоническая

3. средняя геометрическая

Запишем формулы степенных средних, придавая К значения: -1,0,1,2.

При К = -1 получим среднюю гармоническую величину:

При К = 0 получим среднюю геометрическую величину:

Для раскрытия неопределенности прологарифмируем обе части степенной средней:

и подставим К = 0, получим

т.е. неопределенность типа 0 / 0.

Для ее раскрытия используем правило Лопиталя и найдем (lim (ln X)) как предел отношения производных по k числителя и знаменателя в правой части равенства

При k ® 0

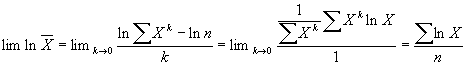
Таким образом, при k= 0,

после потенцирования

При К = 1 получим среднюю арифметическую:

При К= 2 среднюю квадратическую:

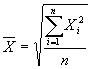
и т.д. для любой степени.

Приведенные выше формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются.

Однако, когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетных формулах степенных средних. В этом случае они называются формулами взвешенных средних и имеют и имеют следующий вид:

средняя гармоническая:

средняя геометрическая:

средняя арифметическая:

средняя квадратическая:

где f i - частота повторения индивидуального значения признака (его вес)

Весом может быть частость, т.е. отношение частоты повторения индивидуального значения признака к сумме частот:

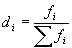
Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. И чем больше показатель степени К, тем больше и величина соответствующей средней:

Это свойства степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних.

30. Структурные средние: мода и медиана. Графическое определение структурных средних

Для характеристики структуры совокупности применяются особые показатели - структурные средние. К таким показателям относятся мода и медиана.

Модой (Мо) называется чаще всего встречающийся вариант.

В дискретном ряду мода- это варианта с наибольшей частотой. В интервальном ряду модой считают центральный вариант модального интервала, т.е. того интервала, который имеет наибольшую частоту (частотность).

Мода для нтервального ряда:

где хм - нижняя граница модального интервала,

д/ - величина модального интервала, /w - частота, соответствующая модальному интервалу.

4 /v/ - частота, предшествующая модальному интервалу, /д/ - частота интервала, следующего за модальным.

Медиана (Me) - это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньше, чем средний вариант, а другая - больше.

Для ранжированного ряда (т.е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом, членов медианой является варианта, расположенная в центре ряда. (Например, данные о стаже работы семи продавцов: 1,2,2,3,5,7,10 - медианой является 4-ая варианта — З г.)

Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных вариант. Например: в бригаде продавцов из 6 человек распределение по стажу работы следующее: 1,3,4,5,7,9 - медиана = (4+5)/2 = 4,5г.

Для интервального вариационного ряда:

Медианный интервал - это интервал, где сумма накопленных частот составляет половину (или больше) всей суммы частот ряда.

Дата добавления: 2014-12-23