
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка качества модели. Прогнозирование
|
|
|
|
Построение тренда методом наименьших квадратов.
Аналитическое выравнивание
Этот метод позволяет построить модель основной тенденции как функцию от времени t (тренд). Коэффициенты модели рассчитываются методом наименьших квадратов.
Задача аналитического выравнивания сводится к следующему – определение на основе фактических данных формы (вида) гипотетической функции 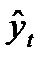 = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выравненных) уровней.
= f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выравненных) уровней.
К качестве моделей наиболее часто применяются функции (таблица 61).
Таблица 61
Функции для модели тренда
| Название функции | Вид функции | Формула |
| Прямая линия | 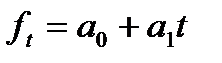 (2) (2)
| |
| Парабола 2-го порядка | или | 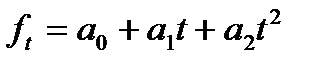
|
| Парабола 3-го порядка | 5 BnGq5yrlDcKN1iCLXP73F0cAAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAA AAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACU AQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA5hxlsZsDAACJ CAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAbJjPed0A AAAHAQAADwAAAAAAAAAAAAAAAAD1BQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAP8G AAAAAA== " path="m,435c130,262,260,90,389,90v129,,251,360,388,345c914,420,1132,77,1212,e" filled="f"> | 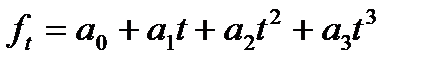
|
| Гипербола | 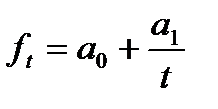
| |
| Показательная | 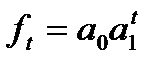
| |
| Степенная | 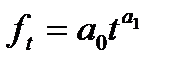
|
Тип модели определяется графически или с помощью абсолютного прироста и темпа роста. Если абсолютные приросты (цепные) приблизительно одинаковы, то берется линейная модель. Если темпы роста приблизительно одинаковы, то берется степенная (возрастает) или гиперболическая (убывает).
Параметры модели ai рассчитываются методом наименьших квадратов, суть которого состоит в том, чтобы сумма квадратов отклонений фактических данных и полученных по модели должна быть минимальна.
При нахождении минимума функции получается системы нормальных уравнений. Для упрощения расчетов показатель времени t задается так, чтобы сумма по времени равнялась 0 (отчет времени с середины ряда динамики). Например:
Уровни t
четное нечетное
y1 -5 -2
y2 -3 -1
y3 -1 0
y4 1 1
y5 3 2
y6 5 ∑t =0
∑t=0
После такого задания времени системы нармальных уравнений для моделей примут вид:
Для линейной модели:
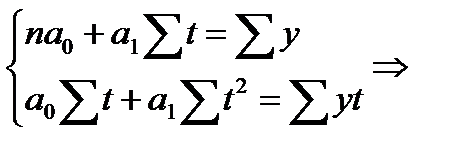
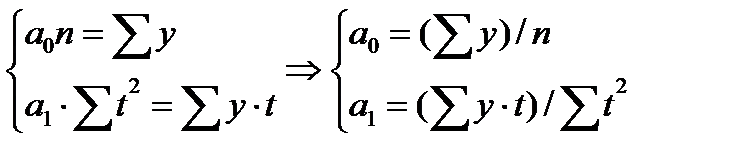 (85)
(85)
Для параболы:
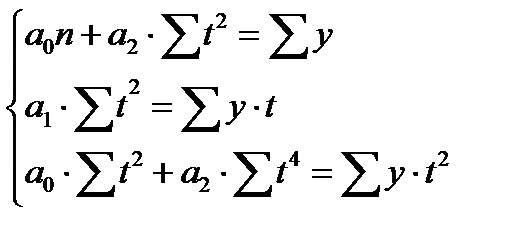 (86)
(86)
Для характеристики качества модели определяют
1) стандартную ошибку модели:
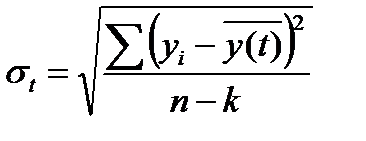 (87)
(87)
n – число уровней
k – число параметров модели.
2) относительную ошибку модели, характеризующую среднюю степень разброса фактических данных вокруг модели:
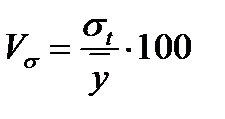 (88)
(88)
Если Vσ < 15%, то модель является хорошей, ее можно использовать для прогнозирования. Для построения прогноза по тренду необходимо в полученную модель подставить будущее значение времени.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 821; Нарушение авторских прав?; Мы поможем в написании вашей работы!