Непрерывность функции. Точки разрыва

ПЕРВЫЙ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

Приведем без доказательства два важных предела, играющих важную роль во многих вопросах математических исследований.

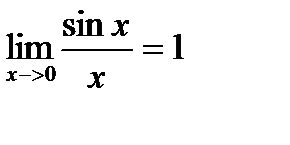
-первый замечательный предел.

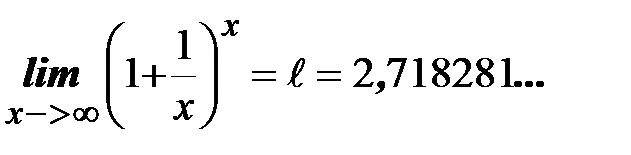
-второй замечательный предел.

Здесь e -иррациональное число.

Если во втором пределе заменить 1/x=a, то a®0 при x®¥, и тогда

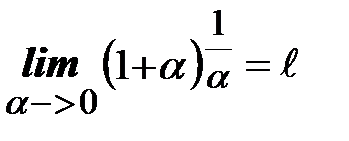
Введем обозначение ln a = log e a. ln a называется натуральным логарифмом. Тогда

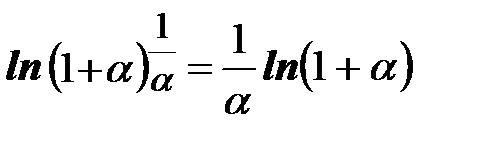
и последний предел можно написать в виде

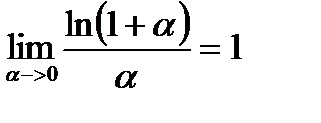
С помощью этих формул вычисляются многие пределы:

Пример 1. Вычислить предел

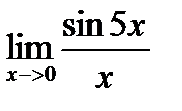
Решение.

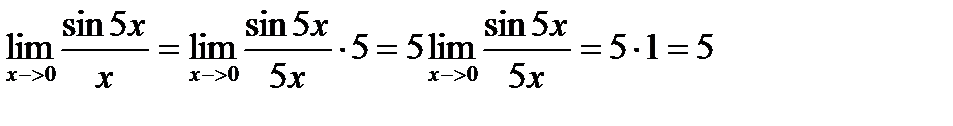
Пример 2. Вычислить предел

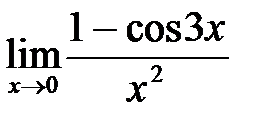
Решение.

Пример 3. Найти предел

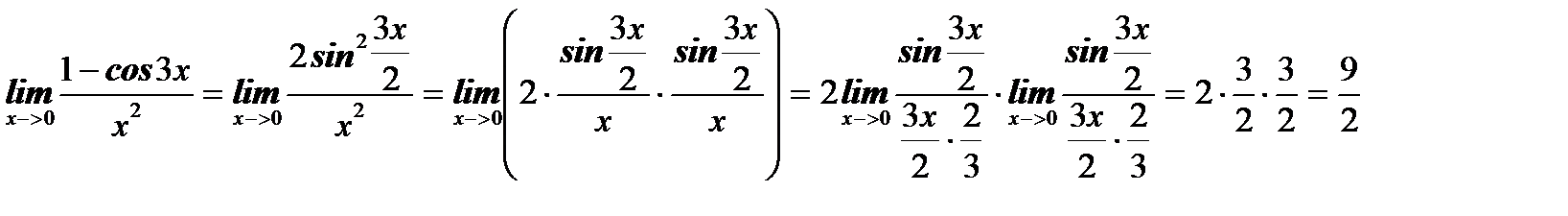
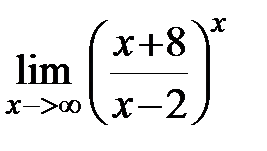
Решение.

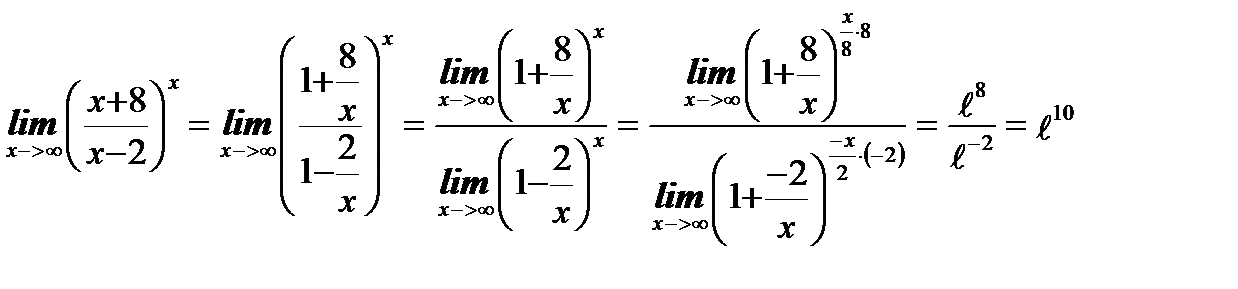
Вычислить пределы функций:

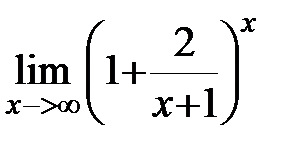
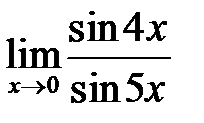1. 2.

Ответ. 1. 4/5; 2. e².

С понятием предела функции тесно связано важное понятие математики - непрерывность функции:

Определение. Говорят, что функция y=f(x) непрерывна в точке x=x₀, если выполняется соотношение:

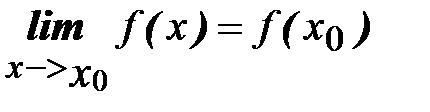
(т.е. предел функции при x®x₀ совпадает со значением функции в этой точке).

Если это соотношение не выполняется, то говорят, что функция y=f(x) имеет разрыв в этой точке (разрывна).

Так, например, все элементарные функции непрерывны в любой точке, где они определены:

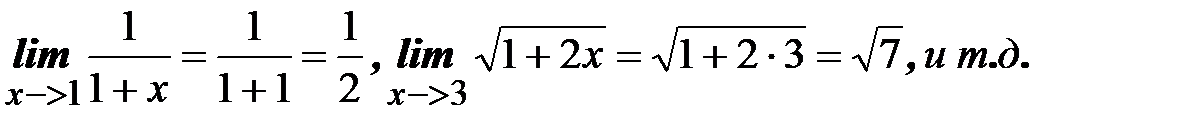
Примером разрывной функции может быть следующая

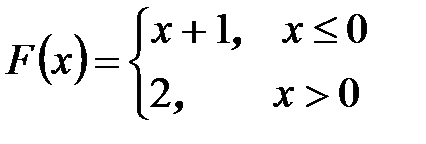
Эта функция разрывна в точке х=0, т.к. f(0)=1, а предел этой функции при х®0 не существует.

Понятие непрерывности функции в точке можно выразить, используя понятие приращения. А именно: приращением Dx₀ в точке x₀ называется разность Dx₀ =x-x₀ => x= x₀+Dx₀.

Приращением функции Dy называется разность Dy = f(x)-f(x₀), которую можно записать следующим образом:

Dy = f(x)-f(x₀)=f(x₀+Dx₀)-f(x₀).

Если x® x₀, приращение аргумента Dx₀ стремится к нулю:

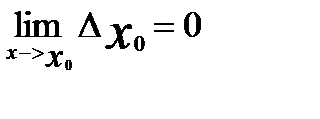
Пусть функция y=f(x) непрерывна в точке x=х₀.Тогда

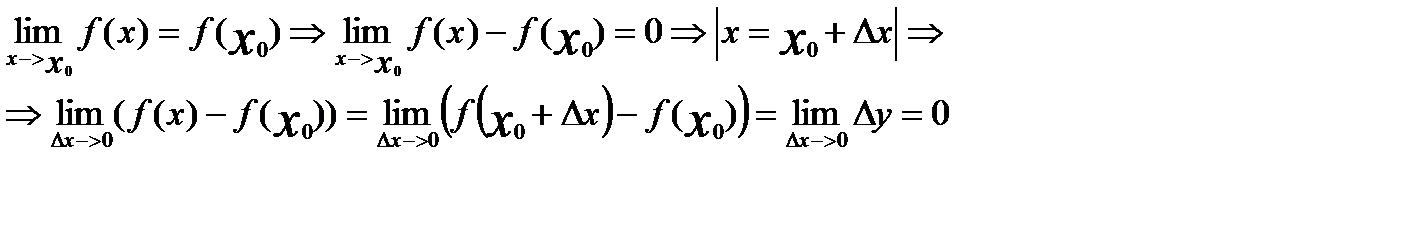
Т.е. можно дать эквивалентное определение: Функция y=f(x) называется непрерывной в точке x=x₀,если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Из определения непрерывности вытекает, что в точке непрерывности

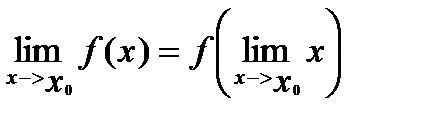
т. е. можно менять местами знаки функции и предела.

Теорема. Если две функции f(x) и g(x) определены и непрерывны в точке

x=x₀,то в этой же точке будут непрерывны функции:

f(x)+g(x); f(x)-g(x); f(x)g(x); f(x)/g(x) (где g(x₀)¹0).

Эта теорема непосредственно вытекает из теоремы о пределе суммы, произведения и частного двух функций.

Определение. Функция y=f(x) называется непрерывной на отрезке [a,b], если она непрерывна в каждой точке этого отрезка.

В точке a она непрерывна справа, т.е.

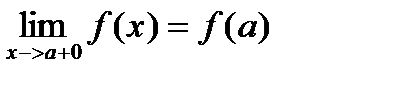
а в точке b непрерывна слева:

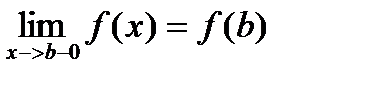
Отметим здесь некоторые свойства функций, непрерывных на отрезке:

1.Если y=f(x) непрерывна на отрезке [a,b], то она достигает своего наибольшего и наименьшего значения на этом отрезке.

2.Если y=f(x) непрерывна на отрезке [a,b] и на концах его принимает значения разных знаков, то на отрезке найдется хотя бы одна точка, в которой f(x)=0.

ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ

Определение. Точка x₀ разрыва функции y=f(x) называется точкой разрыва первого рода, если существуют конечные левый и правый пределы

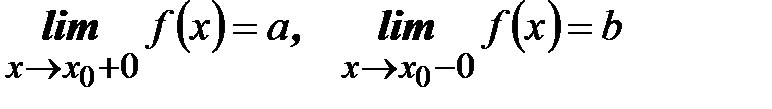
и они не равны между собой. Величина a-b называется скачком

функции в точке x₀.

Пример

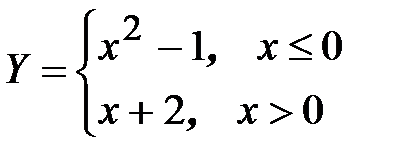
Рассмотрим точку x=0

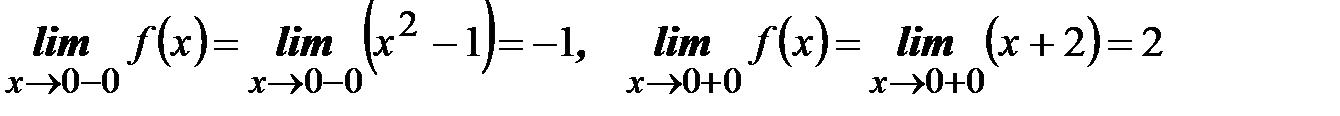
т.е. точка -0 является точкой разрыва первого рода.

Определение. Точка x₀ называется устранимой точкой функции y=f(x), если существуют конечные левые и правые пределы f(x) в этой точке, они равны между собой, но не равны значению функции в этой точке.

Пример.

Рассмотрим точку x=0

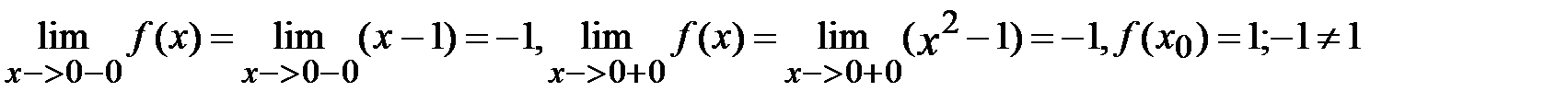
Определение. Если точка x₀ разрыва функции f(x) не является точкой разрыва первого рода или устранимой, она называется точкой разрыва второго рода.

Пример. F(x)=1/x. Рассмотрим точку x=0. Эта точка не входит в область определения функции. Найдем пределы слева и справа.

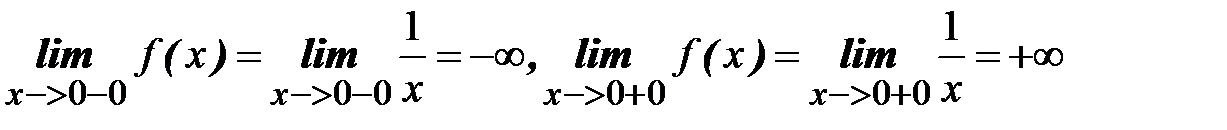
Точка x=0 является точкой разрыва, оба предела равны ¥, следовательно, она является точкой разрыва второго рода.

Пример. Исследовать на непрерывность функцию y=1/(x-1)(x-2) на отрезке [3/2,10].

Решение. Данная функция является элементарной дробно-рациональной функцией, Следовательно она непрерывна во всех точках области определения. Точки x=1и x=2 не входят в область определения функции, точка x=1Ï [3/2,10]. Рассмотрим точку x=2:

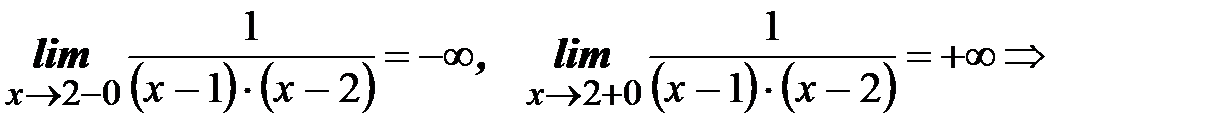
=>Точка x=2 является точкой разрыва второго рода.

Исследовать на непрерывность функции

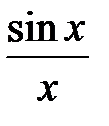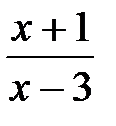1.y= 2.y= 3.y=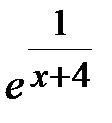

Ответы. 1. Точка x=0 является точкой устранимого разрыва.

2. Точка x=3 является точкой разрыва 2-го рода.

3. Точка x=-4 является точкой разрыва 2-го рода.

Дата добавления: 2014-12-23