
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры для самостоятельного решения
|
|
|
|
Пользуясь формулами дифференцирования, найти производные следующих функций:
 ответ:
ответ: 
 ответ:
ответ: 
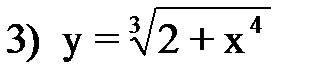 ответ:
ответ: 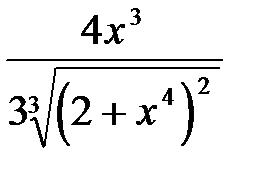
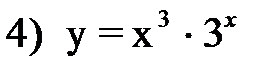 ответ:
ответ: 
 ответ:
ответ: 
 ответ:
ответ: 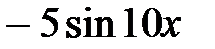
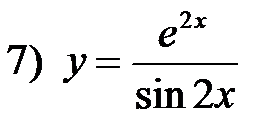 ответ:
ответ: 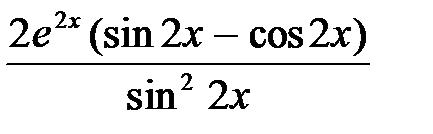
ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Дифференциал функции столь же часто используемое понятие в математике как и производная.
Пусть имеем функцию y=f(x), определенную на интервале (a,b) и непрерывную в точке  . Тогда приращению аргумента
. Тогда приращению аргумента  х отвечает приращение
х отвечает приращение
 у=
у=  f(x0)=f(x0+
f(x0)=f(x0+  x)-f(x0),
x)-f(x0), 
бесконечно малое вместе с  x. Большую роль имеет вопрос: существует ли для
x. Большую роль имеет вопрос: существует ли для  y такая линейная однородная относительно
y такая линейная однородная относительно  х бесконечно малая А
х бесконечно малая А  x (A=const), что их разность оказывается, по сравнению с
x (A=const), что их разность оказывается, по сравнению с  х бесконечно малой высшего порядка малости.
х бесконечно малой высшего порядка малости.
 y=A
y=A  x+
x+  (
( x) (1)
x) (1)
Где о( х) есть величина, стремящаяся к нулю при
х) есть величина, стремящаяся к нулю при  х
х 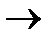 0 быстрее чем
0 быстрее чем  х.
х.
При А  0 наличие равенства (1) показывает, что бесконечно малая А
0 наличие равенства (1) показывает, что бесконечно малая А  х эквивалентна бесконечно малой
х эквивалентна бесконечно малой  у, назовем ее главной частью приращения
у, назовем ее главной частью приращения  у.
у.
Пример.
Рассмотрим функцию у=х3, найдем ее приращения:
 y=(x+
y=(x+  x)3-x3=3x2
x)3-x3=3x2  x+(3x+
x+(3x+  x)(
x)( x)2
x)2
т.е. в данном случае А=3х2, а  ,
,
т.е.  (
( x)=(3x+
x)=(3x+  x)(
x)( x)2.
x)2.
Если равенство (1) выполняется, то выражение А  x называется дифференциалом функции и обозначается символом dy или df(x0)
x называется дифференциалом функции и обозначается символом dy или df(x0)
(в этом обозначении указывается на исходное значение х).
Доказывается, что для того чтобы функция y=f(x) в точке x0 имела дифференциал, необходимо и достаточно, чтобы она была дифференцируема в точке х0 (т.е. имела в этой точке конечную производную 
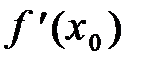 ). При этом А=
). При этом А= 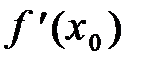 и формула (1) имеет вид:
и формула (1) имеет вид:
 (1a)
(1a)
Итак дифференциал всегда равен
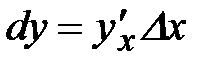 (2)
(2)
Вопрос: Чему равен дифференциал аргумента?

Приращение аргумента(независимой переменной)тождественно равно дифференциалу аргумента.
dx=  x - дифференциал аргумента.
x - дифференциал аргумента.
Если для независимой переменной х имеем dx=  x, то из (2) получим
x, то из (2) получим 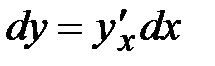 , и следовательно,
, и следовательно,
 производная функции.
производная функции.
Производная функции равна частному дифференциалов функции и аргумента.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 431; Нарушение авторских прав?; Мы поможем в написании вашей работы!