Среднее квадратическое отклонение

Дисперсия

Среднее линейное отклонение

Размах вариации

R=Xmax-Xmin – разница между максимальным и минимальным значением совокупности.

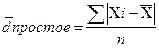
X_i– i-тое значение признака в совокупности,

n – число единиц в совокупности

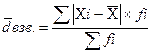
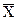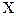- -среднее

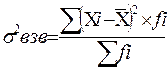
σ=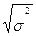

При расчете дисперсии возможно применять способ моментов.

По способу моментов дисперсия рассчитывается по след. формуле:

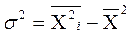
X_i²-средний квадрат значения признака в совокупности.

Показатели размера вариации дают ответ об уровне засоренности в совокупности.

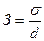
З должна быть≤1,25. Если З>1, 25, то совокупность считается засоренной.

К показателям интенсивностивариации относят коэффициент вариации:

V=

По размаху вариации судят об однородности совокупности.

Если V<30%, то совокупность однородная, если 30% ≤ V ≥ 60%, совокупность средняя, если V > 60%, то совокупность неоднородная.

В том случае, если данные ряда распределения представлены в виде аналитической группировки, рассчитывается общая межгрупповая и внутригрупповые дисперсии.

Общая дисперсия определяет вариацию признака во всей совокупности под влиянием всех факторов, обуславливающих эту вариацию.

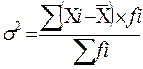
Межгрупповая дисперсия характеризует систематическую вариацию, то есть различия в величине изучаемого признака, возникающего под влиянием признака фактора, положенного в основании группировки.

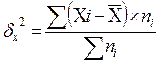, где

X_i и n_i – средние величины численности по отдельным группам.

Внутригрупповая дисперсия отражает случайную вариацию, то есть вариацию, происходящую под влиянием неучтенных факторов.

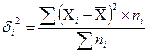
На основании внутригрупповой дисперсии рассчитывается средняя из внутригрупповых дисперсий:

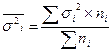
Правило сложения дисперсий:

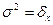
Например, имеются данные о дневной выработке рабочих второго и третьего разряда. Рассчитать внутригрупповую, межгрупповую и общую дисперсии и проверить расчеты по правилу сложения дисперсий.

Второй разряд	Третий разряд
W(X)	X²i	W(X2)	X²2
3,2	10,24	3,9	15,21
4,2	17,64
3,5	12,25	4,8	23,04
5,1	26,01
4,5	20,25	5,4	29,16
6,6	43,56
4,8	23,04
	65,78		154,62

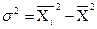
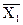
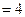
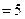
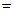
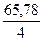
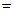
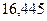
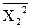
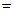
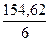
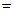
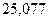
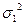
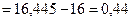
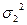
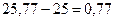
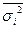
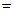
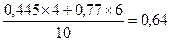
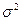
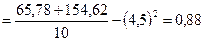
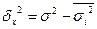
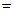
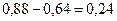
3. Оценка характера распределения предполагает не только оценку однородности, но и оценку симметричности. Симметричным называют распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра, равны между собой.

Степень ассиметричности характеризует коэффициент ассиметрии:

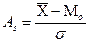
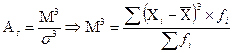
При нормальном распределении коэффициент ассиметрии равен 0, если коэффициент ассиметрии больше 0, то в наличии правосторонняя ассиметрия, если меньше 0, то левосторонняя ассиметрия.

В целом коэффициент ассиметрии может изменяться от –3 до +3.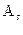

-3≤ ≥3

Если коэффициент ассиметрии показывает нормальное распределение

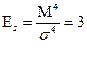
Момент четвертого порядка:

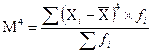
Если Es>0, то распределение островершиное, если Es<0, то плосковершинное.

Выборочной наблюдение

1. Понятие о выборочном наблюдении

2. Способы формирования выборочной совокупности

3. Определение объема выборки и оценка полученных результатов

1.Выборочное наблюдение-это не сплошное наблюдение, при котором обследованию подвергаются величины изучаемой совокупности, отобранные случайным способом.

К основным задачам выборочного наблюдения относят:

1) статистическую проверку гипотез;

2) решение производственных и управленческих задач;

3) отраслевые социально-экономические исследования;

4) разрешение задач в сфере предпринимательской деятельности.

Выборочное наблюдение имеет следующие преимущества перед сплошными:

1) осуществление материальных, финансовых, трудовых ресурсов;

2) сокращаются сроки получения итоговых данных;

3) данный метод дает возможность исследовать процессы,которые не подлежат изучению сплошным методом;

4) повышается точность расчетов.

При проведении выборочного наблюдения вводятся следующие понятия и символы:

1) генеральная совокупность-это совокупность единиц из которых производится отбор

2) выборочная совокупность- это совокупность единиц, отобранных для обследования

3) объем совокупности для генеральной N, для выборочной -n

4) число единиц совокупности для генеральной -M, для выборочной-m

5) доля единиц, обладающих признаком

6) средний размер признака

7) дисперсия

	генеральная	выборочная
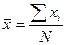
3) 4) 5)   6)     7)	N M W=M/N	n m p=m/n 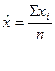  7)

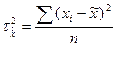
2. Способы отбора групп в выборочнеой совокупности по виду делятся на индивидуальные групповые и комбинированные.

По возможности участия единиц совокупности в отборе, способы подразделяются на повторный и бесповторный.

По процедуре отбора, способы делятся на случайный, механический, типический, серийный и комбинированный.

При осуществлении выборки определяется вероятность возникновения ошибки.

Согласно теореме Чебышева фактическая ошибка не должна превзойти t-кратную ошибку.

На практике, пользуемся правилом 5-ти и 1%-ой ошибки.

Для определения вероятности ее возникновения пользуемся следующей таблицей

t
p					0,997

При повторном отборе и случайном способе формирования выборочной совокупности средняя ошибка определяется по следующей формуле:

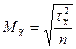
Для доли единиц совокупности расчет ведется по следующей формуле:

Предельная ошибка определяется по формуле:

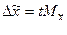
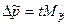
При бесповторном отборе средняя ошибка определяется по следующей формуле:

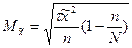
Для доли средняя ошибка рассчитывается

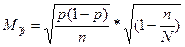
Предел ошибки определяется по тем же самым формулам.

3.Для соблюдения уравнения вероятности возникновения ошибки в выборочной совокупности целесообразно рассчитать число единиц выборочной совокупности.

При повторном отборе число единиц выражается по формуле:

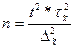
Если данные вырадены в долях, то расчет производится по формуле:

При бесповторном отборе число единиц рассчитывается по формуле:

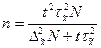
Если данные выражены в долях:

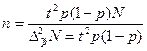
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных выборочного наблюдения.

Чтобы перенести данные на генеральную совокупность, формируют следующее неравенство:

Дата добавления: 2014-12-23