Дисперсия альтернативного признака

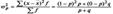
Подст-в в формулу дисперсии q = 1 - р, получим

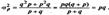
Среднее квад-ое отклонение альтерн-ого признака

Коэффициент вариации представляет собой выраженное в процентах

отношение среднего квадратического отклонения к средней арифметической:: V=

σ / X‾ *100

Общая дисперсия σ² измеряет вариацию признака по

всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она

равна среднему квадрату отклонений отдель­ных значений признака х от общей

средней х и может быть вычислена как простая дисперсия

Межгрупповая дисперсияδ

² характеризует систематиче­скую вариацию результативного признака,

обусловленную влия­нием признака-фактора, положенного в основание группиров­ки.

Она равна среднему квадрату отклонений групповых (част­ных) средних X‾i

от общей средней X‾:

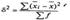
Внутригрупповая (частная) дисперсия σ² i

отражает случай­ную вариацию, т.е. часть вариации, обусловленную влиянием

не­учтенных факторов и не зависящую от признака-фактора, поло­женного в

основание группировки. Она равна среднему квадрату отклонений отдельных

значений признака внутри группы х от средней арифметической этой группы

х) (групповой средней) и может быть исчислена как простая дисперсия

или как взвешенная дисперсия по формулам, соответственно:

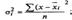
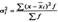
На основании внутригрупповой дисперсии по каждой груп­пе, т.е. на основании

σ² i можно определить общую среднюю извнутригрупповых

дисперсий:

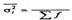
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней

из внутригрупповых и межгрупповой дисперсий:

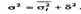
Внутригрупповые дисперсии показывают вариации выработ­ки в каждой группе,

вызванные всеми возможными фактора­ми (техническое состояние оборудования,

обеспеченность ин­струментами и материалами, возраст рабочих, интенсивность

труда и т.д.), кроме различий в квалификационном разряд.

Средняя из внутригрупповых дисперсий отражает вариацию выработки,

обусловленную всеми факторами, кроме квалифика­ции рабочих, но в среднем по

всей совокупности. Межгрупповая дисперсия характеризует вариацию

групповых средних, обусловленную различиями групп рабочих по квали­фикационному

разряду. Общая дисперсия отражает суммарное влияние всех

возмож­ных факторов на общую вариацию среднечасовой выработки изделий всеми

рабочими цеха.

Поэтому в статистическом анализе широко используется эм­пирический

коэффициент детерминации (ή ²) — показатель,

пред­ставляющий собой долю межгрупповой дисперсии в общей дис­персии

результативного признака и характеризующий силу влия­ния группировочного

признака на образование общей вариации:

ή ²=δ² / σ²

Эмпирический коэффициент детерминации показывает долю вариации результативного

признака у под влиянием факторного признака х (остальная часть

общей вариации у обуславливается вариацией прочих факторов). При

отсутствии связи эмпирический коэф равен 0, а при функциональной связи –

единице. Эмпирическое корреляционное отношение — это корень

квад­ратный из эмпирического коэффициента детерминации: _v

ή=√ δ² / σ² оно

показывает тесноту связи между группировочным и ре­зультативным признаками.

Эмпирическое корреляционное отношение ή, как и ή

², может принимать значения от 0 до 1. Если связь отсутствует,

то корреляционное отношение равно нулю, т.е. все групповые средние будут равны

между собой, межгрупповой вариации не будет. Значит, группировочный при­знак

никак не влияет на образование общей вариации. Если связь функциональная, то

корреляционное отношение будет равно единице. В этом случае дисперсия групповых

средних равна общей дисперсии, т.е. внутригрупповой вариации не будет.

Дата добавления: 2014-12-23