
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Преобразуем эмпирический вариационный ряд в интервальный, для этого сначала находим ширину интервала
|
|
|
|
Преобразуем эмпирический вариационный ряд в интервальный, для этого сначала находим ширину интервала, по известной формуле, ранее используемой нами в 1-ом задании
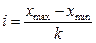 ,
,
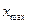 и
и 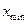 – максимальное и минимальное значение группировочного признака. По нашим данным
– максимальное и минимальное значение группировочного признака. По нашим данным
xmax = 9.3 (млрд.руб.),
xmin= 1.2 (млрд.руб.).
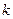 – количество групп, по условию количество групп равно 5.
– количество групп, по условию количество групп равно 5.
Тогда ширина интервала будет
I = (xmax – xmin)/k = (9.3-1.2)5 = 1.6
Теперь можем написать интервальный ряд
Таблица 2.2 – Интервальный ряд
| Объем реализации продукции, работ, услуг, млрд. руб. | Количество предприятий |
| [1,2 – 2.8] | |
| (2,8 – 4,4] | |
| (4,4 – 6] | |
| (6 – 7,6] | |
| (7,6 – 9.3] | |
| Итого |
Определим среднюю величину объема реализации продукции, работ, услуг по интервальному ряду, для этого воспользуемся расчетной таблицей 2.3
Таблица 2.3 – Расчетная таблица
| Группы по объему реализации продукции, работ, услуг, млрд. руб. X | Количество предприятий f | Центр
интервала

| 
|
| 1.2-2-8 | |||
| 2.8-4.4 | 3,6 | 14,4 | |
| 4.4-6 | 5,2 | 20,8 | |
| 6-7.6 | 6,8 | 20,4 | |
| 7.6-9.3 | 8,45 | 25,35 | |
| Итого | - | 92,95 |
Тогда получаем, что средняя величина объема реализации продукции, работ, услуг по интервальному ряду, равна
X0 = ∑xt*f/∑f = 92.95/20 = 4.647
Определяем среднюю величину объема реализации продукции, работ, услуг по интервальному ряду по способу моментов, найдем по формуле
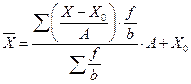 .
.
Для удобства воспользуемся расчетной таблицей 2.4
Таблица 2.4 – Расчетная таблица
Объем реализации продукции, работ, услуг,
млрд. руб.

| Кол-во пред-приятий f |  ,
X0 = 4.77 ,
X0 = 4.77
| 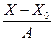 ,
A = 2 ,
A = 2
|  ,
b= 2 ,
b= 2
| 
|
| -2,77 | -1,385 | -4,155 | |||
| 3,6 | -1,17 | -0,585 | -1,17 | ||
| 5,2 | 0,43 | 0,215 | 0,43 | ||
| 6,8 | 2,03 | 1,015 | 1,5 | 1,5225 | |
| 8,45 | 3,68 | 1,84 | 1,5 | 2,76 | |
| Итого | - | - | -0,6125 |
Средняя величина объема реализации продукции, работ, услуг по интервальному ряду по способу моментов равна
X0=∑((x-x0)/A*f/b)/∑f/b) *A+X0 = -0.6125/10*2 + 4.77 = 4.89.
Для расчета моды по интервальному ряду воспользуемся следующей формулой
 ,
,
где 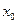 – нижняя граница модального интервала;
– нижняя граница модального интервала;
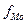 ,
, 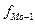 ,
,  – частота соответственно модального, предшествующего модальному и следующего за модальным интервалов.
– частота соответственно модального, предшествующего модальному и следующего за модальным интервалов.
M0 = 4.77 + 1.6*((6-0)/((6-0) + (6-4))) = 5.9
Для расчета медианы по интервальному ряду воспользуемся следующей формулой
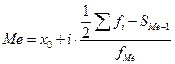 ,
,
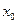 – нижняя граница медианного интервала
– нижняя граница медианного интервала
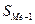 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
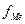 – частота медианного интервала.
– частота медианного интервала.
Для определения медианного интервала рассчитаем накопленные частоты по таблице 2.5
Таблица 2.5 – Расчетная таблица
| Объем реализации продукции, работ, услуг, млрд. руб. | Количество предприятий | Сумма
частот
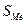
|
| [1,2 – 2.8] | ||
| (2,8 – 4,4] | ||
| (4,4 – 6] | ||
| (6 – 7,6] | ||
| (7,6 – 9.3] | ||
| Итого |
Получили, что медианным интервалом является интервал (2.8 – 4.4), так как Sme = 10. Тогда рассчитаем медиану по интервальному ряду
Me = 2.8 + 1.6*(1/2*20-6)/4 = 4.4
Исчислим все показатели вариации, в т.ч. дисперсию по всем известным формулам, для чего воспользуемся таблицей 2.6
Таблица 2.6 – Расчетная таблица
Объем реализации продукции, работ, услуг,
млрд. руб.

| Кол-во пред-приятий f |  ¯
X = 4.647
¯
X = 4.647
| 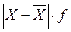
| 
| 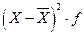
| 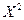
| 
|
| 2,647 | 15,882 | 7,00661 | 42,039654 | ||||
| 3,6 | 1,047 | 4,188 | 1,09621 | 4,384836 | 12,96 | 51,84 | |
| 5,2 | 0,553 | 2,212 | 0,30581 | 1,223236 | 27,04 | 108,16 | |
| 6,8 | 2,153 | 6,459 | 4,63541 | 13,906227 | 46,24 | 138,72 | |
| 8,45 | 3,803 | 11,409 | 14,4628 | 43,388427 | 71,4025 | 214,208 | |
| Итого | - | 40,15 | - | 104,94238 | - | 536,928 |
продолжение таблицы 2.6
 ,
X0 = 4.77 ,
X0 = 4.77
| 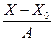 ,
A = 2 ,
A = 2
|  , ,
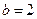
| 
| 
| 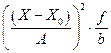
|
| -2,77 | -1,385 | 1,91823 | -4,155 | 5,754675 | |
| -1,17 | -0,585 | 0,34223 | -1,17 | 0,68445 | |
| 0,43 | 0,215 | 0,04623 | 0,43 | 0,09245 | |
| 2,03 | 1,015 | 1,5 | 1,03023 | 1,5225 | 1,5453375 |
| 3,68 | 1,84 | 1,5 | 3,3856 | 2,76 | 5,0784 |
| - | - | - | -0,6125 | 13,155313 |
Показатели вариации равны
1. Размах вариации
R = xmax – xmin = 8.45 – 2 = 6.45 (млрд. руб.);
2. Среднее линейное отклонение
d0 = ∑ |x – x0|*f/∑f = 40.15/20 = 2.01 (млрд. руб.).
3. Дисперсию рассчитаем несколькими способами
3.1. σ2 = ∑ (x-x0)2*f/∑f = 104.942/20 = 5.247
3.2. σ2 = ∑X2*f/∑f – (∑X*f/∑f)2 = 536.928/20 – (4.647)2 = 5.247
3.3. По способу моментов
σ2 = [(∑((X-X0)/A)2*f/b)/ ∑f/b – ((∑((X-X0)/A)*f/b)/ ∑f/b)2]*A2 =
= (13.15/10 – 0.0037)* 22 = 5.247
4. Среднее квадратическое отклонение
σ = 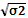 =
= 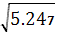 = 2.291 (млрд. руб.).
= 2.291 (млрд. руб.).
5. Коэффициент вариации
ν = σ/x0*100 =2.291/4.77*100 = 48.03%
Можно сделать вывод, что в среднем индивидуальное значение объема реализации продукции, работ, услуг отклоняется от средней величины на 2,01 млрд. руб., а коэффициент вариации говорит о большом разбросе индивидуальных значений объема реализации продукции, работ, услуг от средней. Следовательно, совокупность значений объема реализации продукции, работ, услуг можно назвать неоднородной.
Задание № 3
Используя данные (таблица 3.1) и учитывая, что они получены путем выборочного случайного бесповторного наблюдения из 1000 предприятий отрасли, определить с вероятностью 0,997 в каких пределах будет находиться средняя численность работающих на предприятии в отрасли.
исследовать уровень выполнения норм выработки рабочими предприятия:
1) с вероятностью до 0,997 определить, в каких пределах будет находиться средний процент выполнения норм выработки всеми рабочими предприятия.
2) с вероятность до 0,954 определить, в каких пределах будет находиться доля рабочих, не выполняющих нормы выработки, в целом по предприятию.
Необходимо учитывать, что выработка производилась случайным бесповторным способом из 1000 рабочих предприятия.
Таблица 3.1 – Исходные данные для задания № 3
| № пп | Среднесписочная численность работающих, чел. |
| ИТОГО |
1) Определим по выборке среднесписочную численность работающих
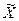 = ∑x/n = 9742/20 = 487.1;
= ∑x/n = 9742/20 = 487.1;
Предельная ошибка выборки находится по формуле
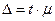
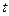 – определяем по таблице, для заданного уровня вероятности, так как
– определяем по таблице, для заданного уровня вероятности, так как 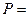 0,997, то
0,997, то 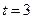 ;
;
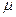 – средняя ошибка выборки, которая для случайной бесповторной выборки рассчитывается по следующей формуле
– средняя ошибка выборки, которая для случайной бесповторной выборки рассчитывается по следующей формуле
 .
.
Найдем среднюю ошибку для нашей выборки:
1) найдем 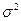 – оценку дисперсии генеральной совокупности по выборке
– оценку дисперсии генеральной совокупности по выборке
σ2 = ∑(x- 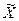 )2/ n-1 = 965959.8/19 = 50839.99;
)2/ n-1 = 965959.8/19 = 50839.99;
2)  – объемы соответственно выборки и генеральной совокупности.
– объемы соответственно выборки и генеральной совокупности.
Тогда средняя ошибка равна
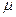 =
= 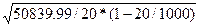 = 49.91;
= 49.91;
Следовательно, предельная ошибка выборки равна
Δ = 3* 49.91 = 149.73.
Можем записать, в каких пределах будет находиться средняя численность работающих на предприятии в отрасли
487.1 – 49.91 ≤ ср. численность работающих ≤ 487,1 + 49,91;
437,19 ≤ ср. численность работающих ≤ 537,01.
С вероятностью 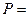 0,997 можем утверждать, что средняя численность работающих на предприятии в отрасли будет находиться на интервале от 437,19 до 537,01 человек.
0,997 можем утверждать, что средняя численность работающих на предприятии в отрасли будет находиться на интервале от 437,19 до 537,01 человек.
Задание № 4
Динамика объема товарной продукции на предприятии характеризуется данными, приведенными в таблице 4.1. Определить цепные и базисные показатели динамики: абсолютный прирост, темп роста, темп прироста, вес одного процента прироста, средний абсолютный прирост, средний темп роста, средний темп прироста.
С помощью метода аналитического выравнивания установить общую тенденцию (определить тренд) изменения объема товарной продукции. Сделать выводы.
Таблица 4.1 – Исходные данные для задания № 4
| Годы | ||||||
| Товарная продукция, млрд. руб. |
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 654; Нарушение авторских прав?; Мы поможем в написании вашей работы!