VI. Показательная модель

V. Степенная модель.

IV. Гиперболическая модель.

Уравнение гиперболической регрессионной модели определяется как 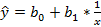. Чтобы свести уравнение к линейному виду, производим замену 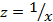. Составим матрицу
.

x	z = 1/x	y	ŷ
		0,00157		-848,636
		0,000344		1873,019
		0,000337		1888,74
		0,000294		1985,65
		0,000283		2009,961
		0,000281		2013,136
		0,000252		2078,504
		0,000251		2080,327
		0,000241		2101,698
		0,000223		2141,98
		0,000178		2241,671
		0,000171		2258,617
		0,00017		2260,353
		0,000145		2316,534
		0,000143		2319,566
		0,000142		2321,465
		0,000141		2325,417
		0,000134		2339,163
		0,000131		2346,89
		0,00013		2348,553
		0,000118		2376,184
		0,000107		2399,476
		0,000107		2400,289
		0,000103		2409,607
		9,93E-05		2417,024
		9,74E-05		2421,041
		8,26E-05		2454,017
		7,01E-05		2481,841
		6,47E-05		2493,797
		5,06E-05		2525,117

По формуле находим В 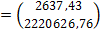, отсюда получаем уравнение 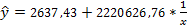. Построим график, на котором изобразим корреляционное облако и уравнение регрессии:

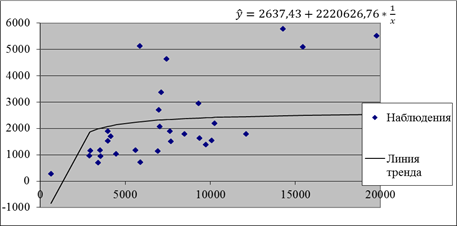
Уравнение степенной регрессионной модели выглядит следующим образом 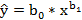. Прологарифмируем его и получим 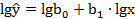. Матрица Х преобразится в
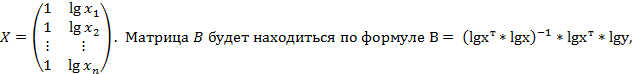где 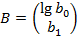. Чтобы получить b_o, нужно 10 возвести в степень lg^bo.

x	lgx	y	lgy	ŷ
		2,804139		2,418301	271,8340246
		3,463146		2,97359	930,6340671
		3,472171		3,052309	946,4518248
		3,532372		2,830589	1059,066922
		3,548881		3,061452	1092,225365
		3,551084		2,962369	1096,728693
		3,599119		3,174932	1199,656346
		3,600537		3,273001	1202,838969
		3,617525		3,22763	1241,608494
		3,651472		3,0086	1322,869537
		3,74904		3,058426	1587,259975
		3,768046		3,708166	1644,607094
		3,770042		2,847573	1650,747952
		3,840106		3,051153	1881,504708
		3,844229		3,429268	1896,04559
		3,846832		3,313445	1905,285356
		3,852297		3,526081	1924,830488
		3,871865		3,663983	1996,468846
		3,883264		3,274158	2039,424406
		3,885757		3,173186	2048,941368
		3,929419		3,246252	2223,006949
		3,969975		3,46568	2397,909847
		3,971461		3,205746	2404,57646
		3,988871		3,134814	2484,038324
		4,003245		3,183839	2551,620773
		4,011232		3,33726	2589,964438
		4,083037		3,247973	2961,621344
		4,154485		3,761025	3384,358351
		4,189209		3,704751	3611,096759
		4,296029		3,740126	4408,316906

Матрица В:

B=	0,160059
	0,811031

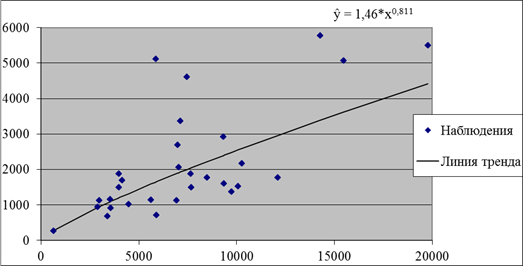
Таким образом, находим b_o = 1,455635 и b₁ = 0,811. Подставляем коэффициенты в уравнение и получаем ŷ = 1,46 * x^0,811. Построим график, содержащий уравнение регрессии, описывающее степенную модель:

Уравнение показательной регрессионной модели имеет вид 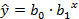, модель строится аналогично степенной. Прологарифмировав уравнением, получаем 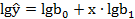. Матрицы X, Y, B, B’ будут выглядеть следующим образом: .

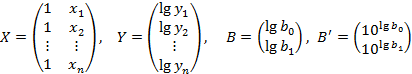x	y	lgy	ŷ
			2,418301	774,7677
			2,97359	1013,847
			3,052309	1021,207
			2,830589	1076,032
			3,061452	1093,007
			2,962369	1095,343
			3,174932	1150,731
			3,273001	1152,506
			3,22763	1174,443
			3,0086	1222,326
			3,058426	1397,43
			3,708166	1439,648
			2,847573	1444,265
			3,051153	1632,085
			3,429268	1644,909
			3,313445	1653,122
			3,526081	1670,661
			3,663983	1736,921
			3,274158	1778,185
			3,173186	1787,487
			3,246252	1968,394
			3,46568	2172,499
			3,205746	2180,759
			3,134814	2282,086
			3,183839	2372,596
			3,33726	2425,795
			3,247973	3019,053
			3,761025	3902,718
			3,704751	4493,125
			3,740126	7491,398

Воспользовавшись формулами, получаем 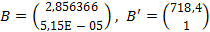. Подставим b₁ и b₀ в уравнение и получаем ŷ = 718,4 * 1^x. Построим график:

Дата добавления: 2014-12-24