РЕШЕНИЕ. Для проверки гипотезы H0 о принадлежности генеральной совокупности нормальному виду распределения необходимо строить интервальный вариационный ряд

Для проверки гипотезы H₀ о принадлежности генеральной совокупности нормальному виду распределения необходимо строить интервальный вариационный ряд, т.к. нормальное распределение является непрерывным. Для этого нужно вычислить размах выборки, который равен разнице между максимальным и минимальным элементами выборки. Кроме того, нужно рассчитать точечные оценки математического ожидания и cреднеквадратического отклонения (СКО).

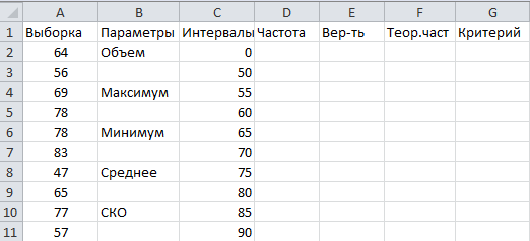
Открываем электронную таблицу и вводим данные выборки в ячейки А2-А41, делаем подписи для расчетных параметров в соответствии с рисунком:

сумма

Вычисляем параметры по выборке. Для этого вводим в ячейку В3: «=СЧЁТ(A2:A41) (=COUNT(A2:A41))»

(здесь и далее кавычки вводить не надо, функции можно вводить с помощью мастера функций из категории «Статистические», как в лабораторной работе № 2, ссылки на ячейки можно ввести щелкнув мышью по ячейке).

В В5 вводим: «=МАКС(A2:A41)( =MAX(A2:A41))»,

в В7: «=МИН(A2:A41)( =MIN(A2:A41))»,

в В9: «=СРЗНАЧ(A2:A41)( =AVERAGE(A2:A41))»,

в В11: «=СТАНДОТКЛОН(A2:A41)( =STDEV(A2:A41))».

Видно, что весь диапазон значений элементов лежит на интервале от 47

до 88. Разобьем этот интервал на интервалы группировки:

[0; 50], (50; 55], (55; 60], (60; 65], (65; 70], (70; 75], (75; 80], (80; 85], (85; 90]. Для этого вводим в ячейки С2-С11 границы интервалов:

ячейка	С2	С3	С4	С5	С6	С7	С8	С9	С10	С11
число

Для вычисления частот пi используем функцию ЧАСТОТА

(FREQUENCY из категории «массив»).

Для этого в D3 вводим формулу

«=ЧАСТОТА(A2:A41;C3:C11) (FREQUENCY(A2:A41;C3:C11))».

В Calc значения частот появятcя сразу для всех интервалов.

В Excel: обводим курсором ячейки D3-D11, выделяя их и нажимаем F2, а затем одновременно Ctrl+Shift+Enter. В результате в ячейках D3-D11 окажутся значения частот.

Для расчета теоретической вероятности pi = F(bi) - F(ai)

вводим в ячейку Е3 разницу между функциями нормального распределения (функция НОРМРАСП (NORMDIST) категории «Статистические»

с параметрами:

«Х» – значение границы интервала, «Среднее» - ссылка на ячейкуВ9, «Стандартное_откл» - ссылка на В11, «Интегральная» - 1.

В результате в Е3 будет формула:

=НОРМРАСП(C3;$B$9;$B$11;1)-НОРМРАСП(C2;$B$9;$B$11;1)

( =NORMDIST(C3;B9;B11;1)-NORMDIST(C2;B9;B11;1))

Автозаполняем эту формулу на Е3-Е10, перемещая нижний правый

угол Е3 до ячейки Е10.

В последней ячейке столбца Е11 для соблюдения условия нормировки вводим дополнение предыдущих вероятностей до единицы. Для этого вводим в Е11: «=1-СУММ(E3:E10)» (можно без нормировки)

Для расчета теоретической частоты n_i′ = np_i вводим в F3 формулу: «=E3*$B$3», автозаполняем ее на F3-F11.

Для вычисления элементов суммы 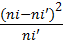критерия Пирсона

вводим в G3 значение «=(D3-F3)*(D3-F3)/F3» и автозаполняем его на

диапазон G3-G11.

Находим значение критерия 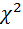и критическое значение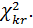

Для этого вводим в F12 подпись «Сумма», а в F13 подпись «Критич.».

Вводим в соседние ячейки формулы –

в G12: «=СУММ(G3:G11) (=SUM(G3:G11))»,

а в G13: «=ХИ2.ОБР.ПХ(0,05;6) (=CHIINV(0,05;6))»,

здесь параметр α= 0,05 взят из условия, а степень свободы (k-r-1)=(9-2-1)=6, так как k=9 – число интервалов группировки, а r=2, т.к. были оценены два параметра нормального распределения: математическое ожидание и СКО.

Видно, что 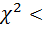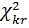, следовательно гипотеза H₀ принимается, то есть можно считать, что ЧСС у данной группы больных распределена по нормальному закону распределения.

Наглядно увидеть это можно, построив графики плотностей эмпирического и теоретического распределений.

Ставим курсор в любую свободную ячейку и вызываем мастер диаграмм (Вставка/Диаграмма). Выбираем тип диаграммы «График» и вид «График с маркерами» самый левый во второй строке, нажимаем «Далее».

Ставим курсор в поле «Диапазон» и удерживая кнопку CTRL обводим мышью область ячеек D3-D11 а затем F3-F11. Переходим на закладку «Ряд» и в поле «Подписи оси Х» обводим область С3-С11. Нажимаем «Готово». Видно, что графики достаточно хорошо совпадают, что говорит о соответствии данных нормальному закону.

Задание. Проверить по критерию Пирсона на уровне значимости α = 0,02 статистическую гипотезу о том, что генеральная совокупность, представленная выборкой, имеет нормальный закон распределения.

Данные взять из задания 4 лабораторной работы № 1.

Вариант Выборка

1. 45 52 49 48 42 51 54 54 50 47 56 53 59 57 50

45 50 46 55 46 54 55 64 67 51 49 47 47 55 40

2. 48 43 52 42 38 57 47 47 51 52 55 53 50 46 53

50 49 58 53 44 51 49 53 51 51 48 45 46 49 54

3. 65 81 76 84 81 80 78 86 85 83 75 85 83 80 77

69 73 78 75 75 91 79 74 67 68 78 80 81 81 81

4. 75 82 79 78 72 81 84 84 80 77 86 83 89 87 80

75 80 76 85 76 84 85 94 97 81 79 77 77 85 70

5. 78 73 82 72 68 87 77 77 81 82 85 83 80 76 83

80 79 88 83 74 81 79 83 81 81 78 75 76 79 84

6. 70 59 57 62 49 63 59 60 57 66 64 57 59 58 59

56 62 56 57 63 59 55 58 62 61 60 59 59 61 63

7. 39 41 35 41 42 38 41 41 36 45 40 39 41 41 40

42 45 39 39 35 41 36 36 39 41 43 40 41 38 44

8. 15 31 26 34 31 30 28 36 35 33 25 35 33 30 27

19 23 28 25 25 41 29 24 17 18 28 30 31 31 31

9. 25 32 29 28 22 31 34 34 30 27 36 33 39 37 30

25 30 26 35 26 34 35 44 47 31 29 27 27 35 20

10. 59 60 65 50 55 64 66 63 55 62 60 58 67 58 65

63 59 57 65 56 66 59 59 60 61 65 59 50 64 63

11. 40 41 37 37 40 42 39 43 38 41 45 44 48 43 28

39 41 39 38 44 37 41 42 45 40 43 35 44 44 44

12. 54 59 55 57 44 42 52 55 49 53 51 50 61 59 53

46 47 44 52 49 48 56 40 52 46 46 45 52 59 57

Дата добавления: 2014-12-24