Часть 2. Интервальное оценивание

Точечные оценки являются лишь приближенным значением неизвестных параметров генеральной совокупности. Чтобы получить представление о точности и надежности оценки используют интервальную оценку параметра.

Интервальной оценкой параметра θ называется числовой интервал (a,b) который с заданной вероятностью p покрывает неизвестное значение параметра θ.

Такой интервал (a,b) называется доверительным, а вероятность p доверительной вероятностью. Вместо нее часто задают величину α =1- p, называемую уровнем значимости.

Рассмотрим теперь методы интервального оценивания.

Если выборка объема п представляет случайную величину, распределенную нормально, то доверительный интервалы для математического ожидания:

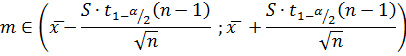
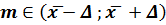
Для дисперсии:

где 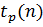и 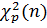- квантили распределения Стьюдента и хи-квадрат,

=1- p.

Электронная таблица Excel (Calc), содержащая встроенные статистические функции позволяет легко и быстро найти доверительные интервалы для математического ожидания и дисперсии. Рассмотрим решение этой задачи.

Возвращаемся на лист 1 электронной таблицы с данными

примера и для них вычислим доверительные интервалы при р =0,95.

Вводим данные согласно рисунку:

Для вычисления величины служит функция «ДОВЕРИТ»(«CONFIDENCE») категории «Статистические» с тремя параметрами «Альфа» - уровень значимости =1- p,

«Станд_откл» - среднеквадратическое отклонение S,

«Размер» - объем выборки п.

Таким образом, вводим в Н3 функцию:

=СРЗНАЧ(А1:А25)-ДОВЕРИТ(I1;СТАНДОТКЛОН(А1:А25);25)

(=AVERAGE(A1:A25)-CONFIDENCE(I1;STDEV(A1:A25);25))

а в ячейку I3 функцию:

=СРЗНАЧ(А1:А25)+ДОВЕРИТ(I1;СТАНДОТКЛОН(А1:А25);25)

(=AVERAGE(A1:A25)+CONFIDENCE(I1;STDEV(A1:A25);25))

Для вычисления доверительного интервала для дисперсии следует отметить, что функция вычисления квантили распределения хи-квадрат

(обратного распределения хи-квадрат) называется «ХИ2ОБР» («СHIINV»)

(категория «Статистические») и имеет два параметра:

первый «Вероятность» содержит доверительную вероятность р,

второй – степень свободы п -1.

Для вычисления левой границы доверительного интервала для дисперсии

в ячейку Н4 вводим запись:

=ДИСП(A1:A25)*24/ХИ2ОБР(0,025;24)

(=VAR(A1:A25)*24/CHIINV(0,025;24))

Для вычисления левой границы доверительного интервала для дисперсии

а в ячейку I4 запись:

=ДИСП(A1:A25)*24/ХИ2ОБР(0,975;24)

(=VAR(A1:A25)*24/CHIINV(0,975;24))

.

Получаем значения границ доверительных интервалов.

Задание 2 к лабораторной работе №2.

1. Для выборки вашего варианта (задание 1) вычислить доверительные интервалы для математического ожидания и дисперсии при = 0,01.

2. Изменяя значение уровня значимости 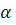сделать вывод о его влиянии на ширину интервала. Вывод записать.

Контрольные вопросы:

1. Что называют точечной оценкой параметра распределения?

2. Дайте определения таким понятиям как: выборочная средняя, выборочная дисперсия, стандартное отклонение, мода, медиана, ассиметрия, эксцесс, процентиль.

3. Что называют интервальной оценкой?

4. Что такое доверительный интервал?

5. Как вычисляется доверительная вероятность и уровень значимости?

Дата добавления: 2014-12-24