Звено 8

Y(S) =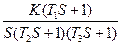

а) K = 10, Т1 = 0.1, T2=0.5, T3=1

- переходные процессы с помощью преобразования Лапласа;

Для начала исследования переходного процесса с помощью преобразования Лапласа необходимо получить обратное преобразование Лапласа передаточной функции звена и представить его графически.

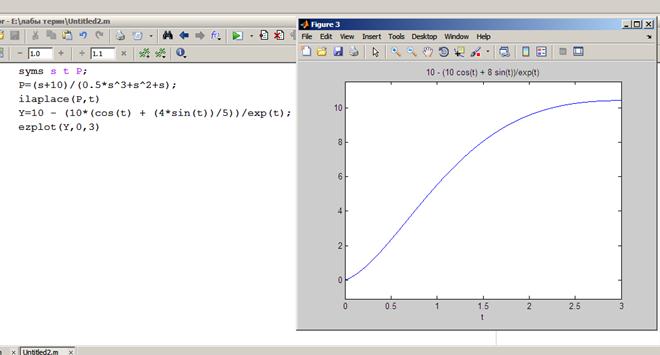
- реакция звена на единичное ступенчатое воздействие;

Для вычисления реакции звена на единичное ступенчатое воздействие используется функция step().

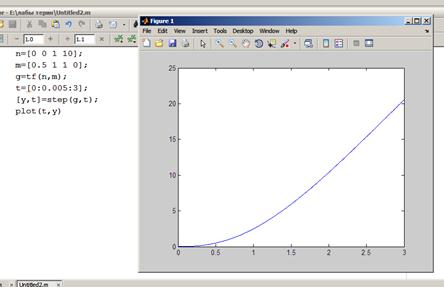
- амплитудно-частотная и фазочастотная характеристики;

АЧ и ФЧ характеристики строятся с помощью функции bode().

- амплитудно-фазовая характеристика;

АФ характеристику называют диаграммой Найквиста.

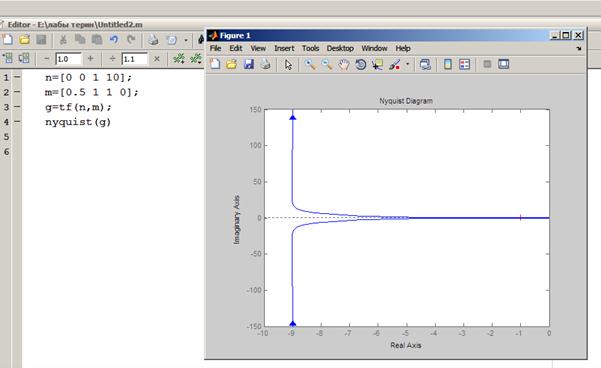
- диаграмма Никольса;

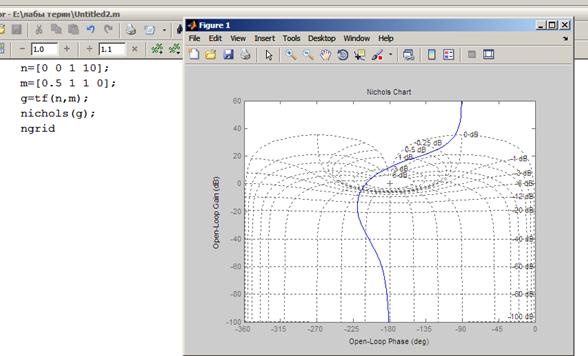
- показатели качества переходного процесса (вид переходного процесса и его длительность, величину перерегулирования);

Нули и полюса

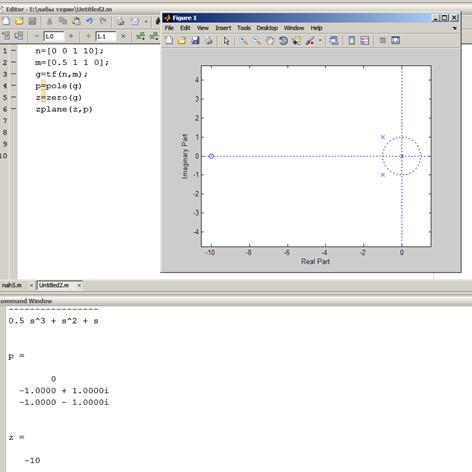
Функция feedback(),

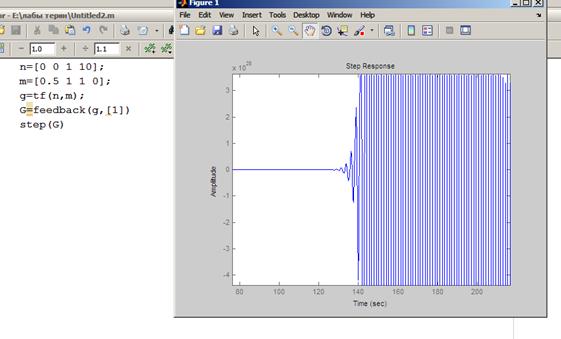
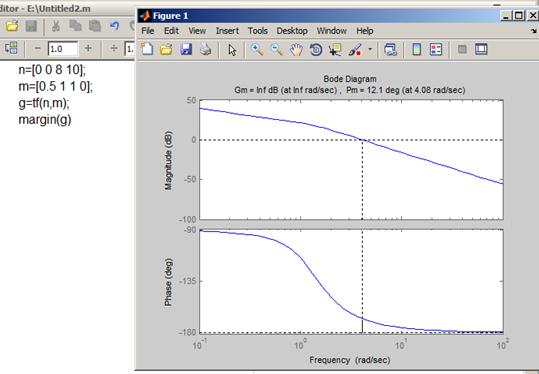
Длительность переходного процесса t=5.5 сек., величина перерегулировании А=1,05.

- запас устойчивости по амплитуде и фазе;

Функция margin().

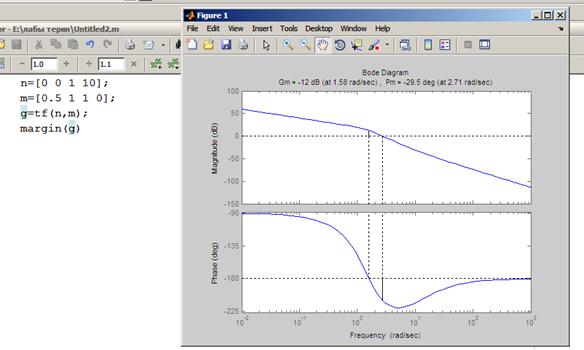
б) K = 10, T1=0.8, T2=0.5, T3=1.

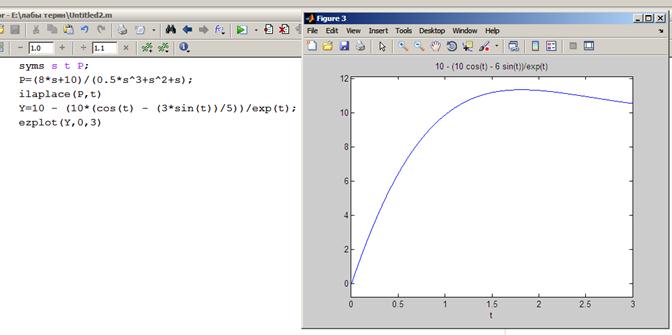
- переходные процессы с помощью преобразования Лапласа;

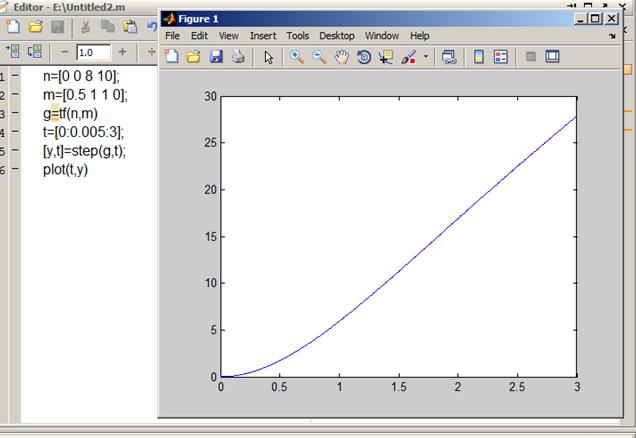
- реакция звена на единичное ступенчатое воздействие;

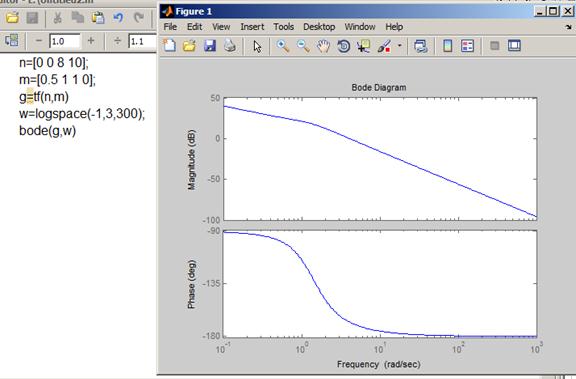
- амплитудно-частотная и фазочастотная характеристики;

- амплитудно-фазовая характеристика;

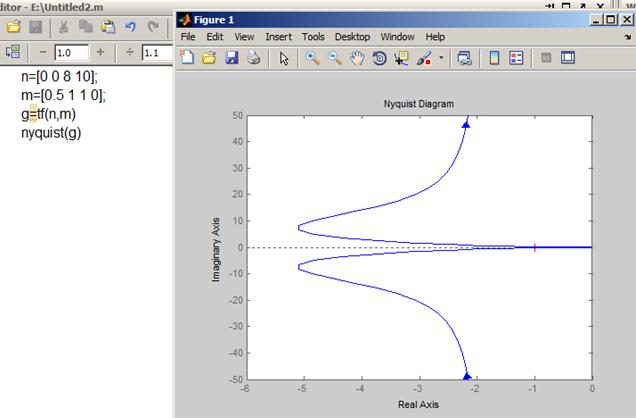
- диаграмма Никольса;

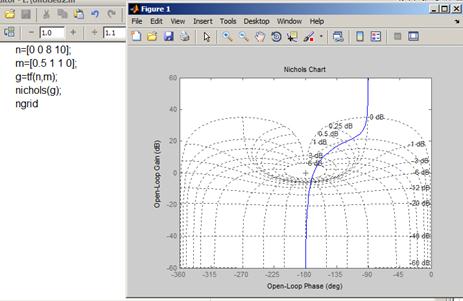
- показатели качества переходного процесса (вид переходного процесса и его длительность, величину перерегулирования);

Нули и полюса

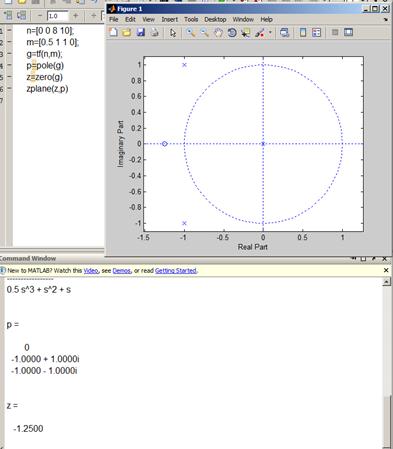
Функция feedback(),

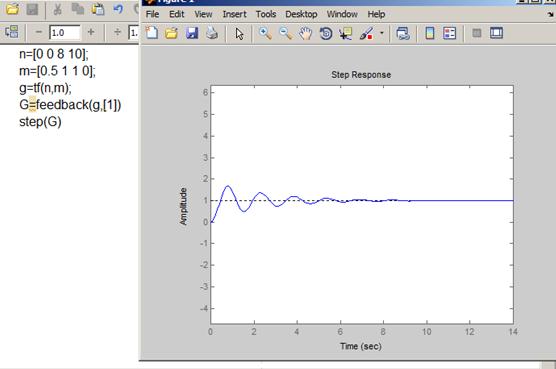
Длительность переходного процесса t=8.5 сек., величина перерегулировании А=1.7.

- запас устойчивости по амплитуде и фазе;

Звено 10:

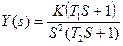
a)K=20, T₁=0.5, T₂=1

1 переходные процессы с помощью преобразования Лапласса

n=[10 20];

m=[1 1 0 0];

g=tf(n,m)

syms s t H;

H=laplace(H,t)

Результат:

g =

10 s + 20

---------

s^3 + s^2

Continuous-time transfer function.

H =

1/t^2

2 Реакция звена на единичное ступенчатое воздействие

step(g)

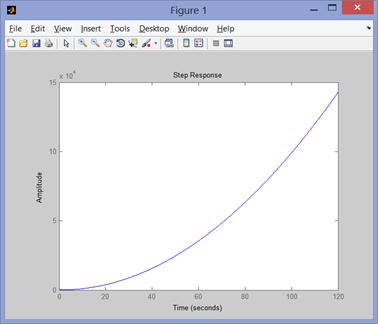
Рис. 78 Реакция звена на единичное ступенчатое воздействие

3 Амплитудно-частотная и фазо-частотная характеристика

bode(g)

w=logspace(-1,3,200)

bode(g,w)

Результат:

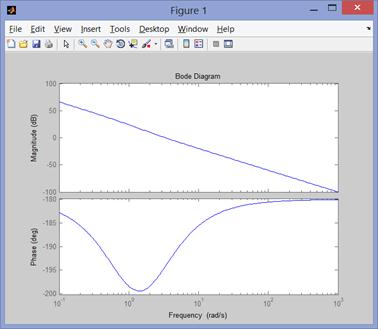
Рис. 79 Амплитудно-частотная и фазо-частотная характеристика

4 Амплитудно-фазовая характеристика

nyquist(g)

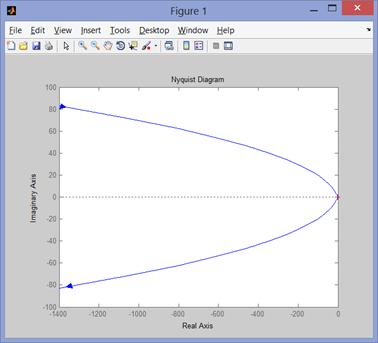
Рис. 80 Амплитудно-фазовая характеристика

5 Диаграмма Никольса

w=logspace(-1,1,400)

nichols(g,w)

grid on

Результат:

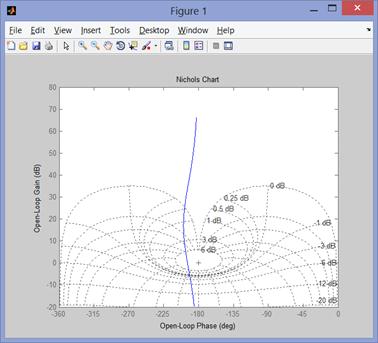
Рис. 81 Диаграмма Никольса

6 Показатели качества переходного процесса(вид переходного процесса, его длительность и величина перерегулирования)

p1=pole(g)

z1=zero(g)

pzmap(g)

Результат:

p1 =

-1

z1 =-2

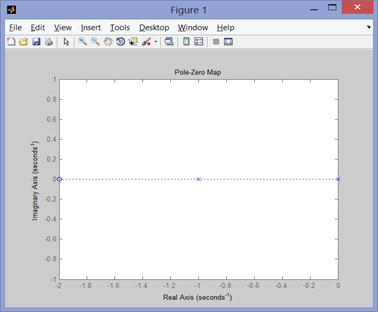
Рис. 82нули и полюса

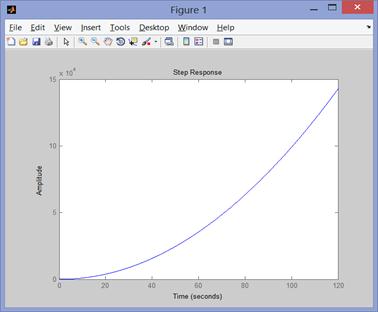
Рис. 83реакция системы

Этот график иллюстрирует реакцию системы на ступенчатую функцию во времени.

График является апериодическим с длительностью в 120 секунды и перерегулированием равным 15

7 Запас устойчивости по амплитуде и фазе

gos=feedback(g,1)

p2=pole(gos)

z2=zero(gos)

pzmap(gos)

Результат:

gos =

10 s + 20

---------------------

s^3 + s^2 + 10 s + 20

Continuous-time transfer function.

p2 =

0.3815 + 3.3466i

0.3815 - 3.3466i

-1.7629

z2 =-2

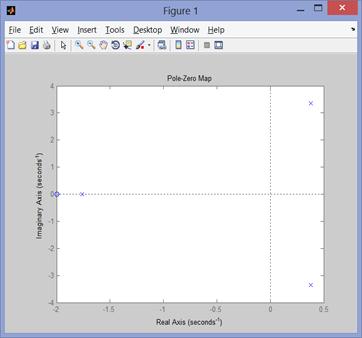
Рис. 84нули и полюса

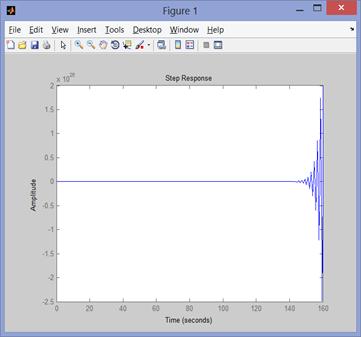
Рис. 85реакция системы

Этот график иллюстрирует реакцию системы на ступенчатую функцию во времени.

График является апериодическим с длительностью в 160 секунд и перерегулированием равным 2

б) K=20 T₁=1, T₂=0.5

1 переходные процессы с помощью преобразования Лапласса

n=[20 20];

m=[0.5 1 0 0];

g=tf(n,m)

syms s t H;

H=laplace(H,t)

Результат:

g =

20 s + 20

-------------

0.5 s^3 + s^2

Continuous-time transfer function.

H =

1/t^2

2 Реакция звена на единичное ступенчатое воздействие

step(g)

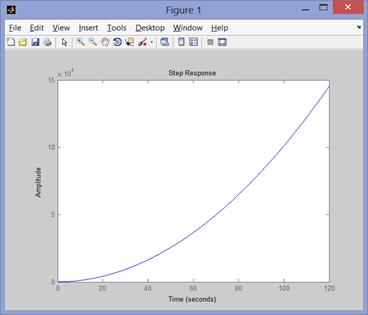
Рис.86 Реакция звена на единичное ступенчатое воздействие

3 Амплитудно-частотная и фазо-частотная характеристика

bode(g)

w=logspace(-1,3,200)

bode(g,w)

Результат:

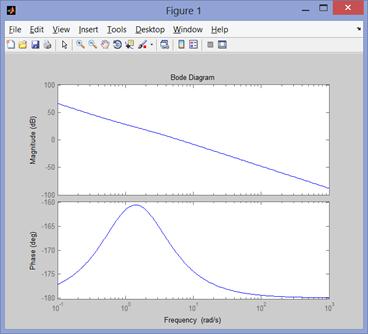
Рис. 87 Амплитудно-частотная и фазо-частотная характеристика

4 Амплитудно-фазовая характеристика

nyquist(g)

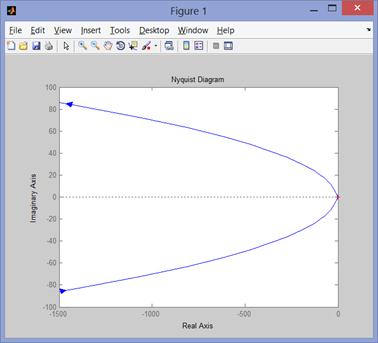
Рис. 88 Амплитудно-фазовая характеристика

5 Диаграмма Никольса

w=logspace(-1,1,400)

nichols(g,w)

grid on

Результат:

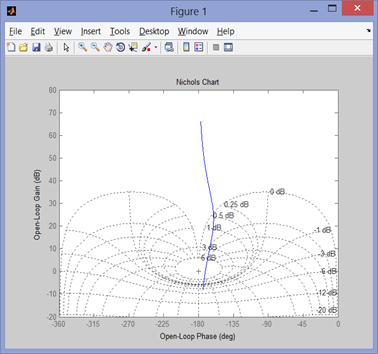
Рис. 89 Диаграмма Никольса

6 Показатели качества переходного процесса(вид переходного процесса, его длительность и величина перерегулирования)

p1=pole(g)

z1=zero(g)

pzmap(g)

Результат:

p1 =

-2

z1 = -1

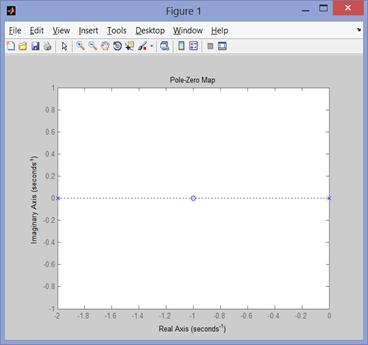
Рис. 90нули и полюса

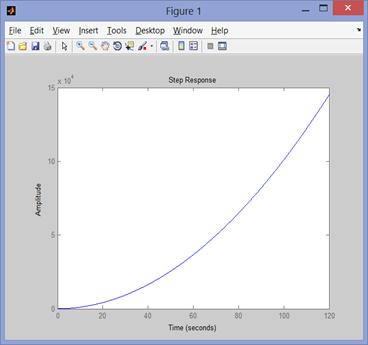
Рис. 91 реакция системы

Этот график иллюстрирует реакцию системы на ступенчатую функцию во времени.

График является апериодическим с длительностью в 120 секунд и перерегулированием равным 15

7 Запас устойчивости по амплитуде и фазе

gos=feedback(g,1)

p2=pole(gos)

z2=zero(gos)

pzmap(gos)

Результат:

gos =

20 s + 20

-------------------------

0.5 s^3 + s^2 + 20 s + 20

Continuous-time transfer function.

p2 =

-0.4872 + 6.2260i

-0.4872 - 6.2260i

-1.0256

z2 =-1

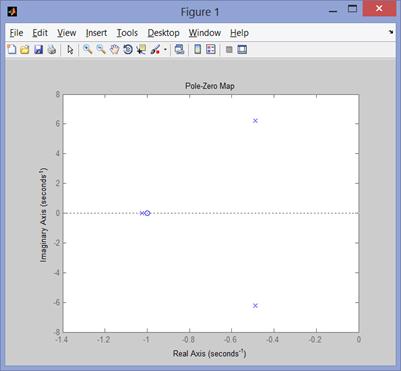
Рис. 92 нули и полюса

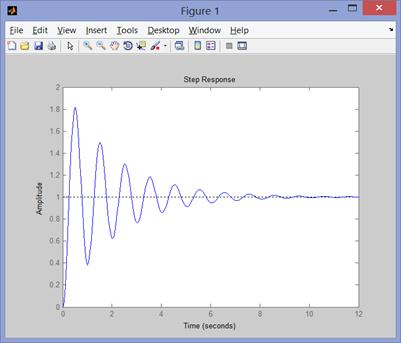
Рис. 93 реакция системы

Этот график иллюстрирует реакцию системы на ступенчатую функцию во времени.

График является апериодическим с длительностью в 12 секунд и перерегулированием равным 2

Заключение

Теория управления — наука о принципах и методах управления различными системами, процессами и объектами. Суть теории управления состоит в построении математической модели на основе системного анализа объекта управления и синтезе алгоритма управления для получения желаемых характеристик протекания процесса или целей управления.

В данной курсовой работе рассмотрены основы теории управления с помощью программ VisSim и MatLab. С помощью их мы исследовали различное поведение функций. Научились определять устойчивость системы.

В моём задании система была устойчива, по причине нахождения нулей и полюсов в левой полуплоскости. Так же во второй части задания я находил придаточные функции, исследовал их и находил дифференциальное уравнение.

Список литературы

1. Лукас В. А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.

2. Брюханов В. Н. и др. Теория автоматического управления. –М: Высшая школа, 2000 г.

3. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. - M.: Наука, 1975.

4. Острём К., Виттенмарк Б. Системы управления с ЭВМ: Пер. с англ. - М.: Мир, 1987. - 480 с., ил.

5. Оппенгейм Э., Шафер Р. Цифровая обработка сигналов/ Пер. с англ./ Под ред. С. Я. Шаца. - М.: Связь, 1979. - 416 с.

6. Антонью А. Цифровые фильтры: анализ и проектирование/ Пер. с англ. - М.: Радио и связь, 1983. - 320 с.

7. Гольденберг Л. М., Матюшкин Б. Д., Поляк М. Н. Цифровая обработка сигналов: Справочник. - М.: Радио и связь, 1985. -312 с., ил.

8. Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения: В 2 т./ Пер. с англ. Ф. М. Писаренко с предисловием А. М. Яглома - М.: Мир, 1971.

9. Сборник задач по теории автоматического регулирования и управления/ Под редакцией В. А. Бесекерского. - M.: Наука, 1978.

Дата добавления: 2014-12-24