
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение седловой точки
|
|
|
|
1. Запишем функцию Лагранжа (3.20), для чего составим линейную комбинацию заданных целевой функции и левых частей ограничений – неравенств, умноженных на дополнительные неизвестные – множители Лагранжа 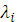 ,
,  , в соответствии с постановкой задачи (3.5), (3.6):
, в соответствии с постановкой задачи (3.5), (3.6):
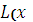 ; λ)=
; λ)= 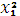 +
+ 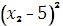 +
+ 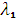 (2
(2  - 5
- 5  +7)+
+7)+  (
( 3
3  +15)+
+15)+  (4
(4  +7
+7 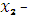 71). (3.26)
71). (3.26)
2. Находим частные производные:
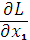 = 2
= 2  + 2
+ 2 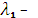 3
3  + 4
+ 4  , (3.27)
, (3.27)
 = 2(
= 2(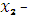 5)
5)  5
5 
 +7
+7  , (3.28)
, (3.28)
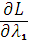 = 2
= 2 
 5
5 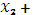 7, (3.29)
7, (3.29)
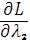 =
=  3
3 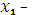
 +15, (3.30)
+15, (3.30)
 = 4
= 4  +7
+7 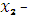 71. (3.31)
71. (3.31)
3. Используем условия (3.24) и (3.25). Поскольку  = 3,
= 3,  = 6, то для выполнения условия
= 6, то для выполнения условия 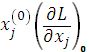 = 0 требуется, чтобы
= 0 требуется, чтобы  = 0, поэтому из (3.27) следует
= 0, поэтому из (3.27) следует
2  + 2
+ 2  3
3 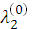 +4
+4  = 0 (3.32)
= 0 (3.32)
или 2 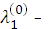 3
3 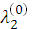 + 4
+ 4  =
=  6.
6.
Аналогично из (3.28) имеем:
 5
5 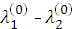 +7
+7  =
=  2 (3.33)
2 (3.33)
4. Анализируем (3.25).
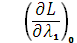 = 2
= 2 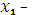 5
5 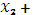 7= 2
7= 2 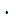 3
3  5
5 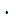 6 +7
6 +7  .
.
Следовательно, для выполнения  = 0 необходимо, чтобы
= 0 необходимо, чтобы  = 0.
= 0.
Аналогично, поскольку
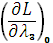 = 4
= 4  +7
+7  71= 4
71= 4 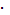 3 + 7
3 + 7 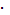 6
6  71≠ 0, то
71≠ 0, то  = 0.
= 0.
В то же время 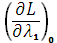 =
=  3
3 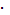
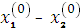 + 15=
+ 15=  3
3 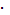 36 + 15 = 0, следовательно
36 + 15 = 0, следовательно 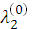 может быть не равным 0.
может быть не равным 0.
5. Из (3.32) и (3.33) находим 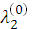 :
:
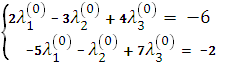
 = 0,
= 0,  = 0.
= 0.
Очевидно, что
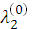 = 2.
= 2.
6. Таким образом, искомая седловая точка имеет координаты:
(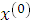 ,
, 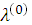 ) = (3; 6; 0; 2; 0).
) = (3; 6; 0; 2; 0).
7. Проверка. Седловая точка (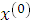 ,
, 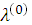 ) должна соответствовать условию (3.22).
) должна соответствовать условию (3.22).
Имеем:
 (
(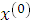 , λ)= 10
, λ)= 10  17(
17(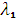 +
+  ),
),
 (
(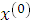 ,
, 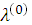 )= 10,
)= 10,
 (
(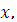
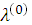 ) =
) = 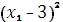 +
+  +10.
+10.
Поскольку
 (
(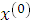 , λ) <
, λ) < 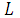 (
(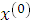 ,
, 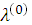 ) =
) =  (
(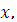
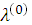 ),
),
условие выполнено.
8. Ответ: (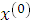 ,
,  ) = (3; 6; 0; 2; 0).
) = (3; 6; 0; 2; 0).
Задача №4
Двум предприятиям  и
и  выделено
выделено  = 1000 денежных единиц средств на 4 года.
= 1000 денежных единиц средств на 4 года.
Как распределить эти средства между предприятиями в начале каждого года их работы, например, предприятию  выделить
выделить  средств, предприятию
средств, предприятию 

 средств,
средств,  = 1, 2, 3, 4,
= 1, 2, 3, 4,  , чтобы общий доход за 4-х летний период был бы максимальным, если известно, что предприятие
, чтобы общий доход за 4-х летний период был бы максимальным, если известно, что предприятие  за один год работы обеспечивает доход
за один год работы обеспечивает доход 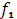 (
( ) = 5
) = 5  и остаток к концу года
и остаток к концу года 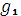 (
( ) = 0,3
) = 0,3  , а предприятие
, а предприятие  , соответственно,
, соответственно, 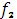 (
( )= 4
)= 4  и
и  (
( )= 0,5
)= 0,5  .
.
Задачу решить методом динамического программирования.
Анализ условия задачи
Основные теоретические сведения: Принцип оптимальности Беллмана. Функциональные (рекуррентные) уравнения динамического программирования.
По условию задачи на 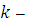 м году работы в результате распределения средств
м году работы в результате распределения средств 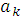 на величины
на величины  и
и  получим доход
получим доход 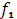 (
( ) и остаток средств
) и остаток средств 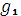 (
( ) от первого предприятия
) от первого предприятия  и, соответственно,
и, соответственно, 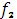 (
( ) и
) и  (
( ) от предприятия
) от предприятия  . Очевидно, что для дальнейшего распределения на
. Очевидно, что для дальнейшего распределения на  +1 – й год имеем
+1 – й год имеем 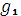 (
( ) +
) +  (
( ) средств, остаток от которых в конце
) средств, остаток от которых в конце  +1
+1  го года перейдет на
го года перейдет на  +2
+2  й год и опять будет перераспределён. Заданные функции
й год и опять будет перераспределён. Заданные функции 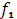 (
( ),
), 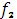 (
( ),
), 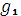 (
( ),
),  (
( ), k =1, 2, 3, 4, где
), k =1, 2, 3, 4, где 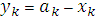 , определены в области 0 ≤
, определены в области 0 ≤  ≤
≤  , а функция
, а функция 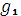 (
( ) +
) +  (
( ) удовлетворяет неравенству 0 ≤
) удовлетворяет неравенству 0 ≤ 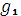 (
( )+
)+  (
( ) ≤
) ≤  .
.
Задача заключается в том, чтобы построить оптимальное управление по перераспределению между двумя предприятиями остающихся средств, позволяющее получить максимально возможный общий доход после 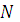 = 4
= 4 
 этапного 4 шагового процесса перераспределения средств.
этапного 4 шагового процесса перераспределения средств.
Максимальное значение целевой функции 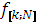 (
( ,
,  ,
, 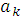 ),
), 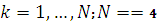 получаем в результате построения оптимального управления шаг за шагом. Целевая функция выражает общий доход двух предприятий к концу 4-х лет работы в зависимости от выделяемых каждому предприятию средств
получаем в результате построения оптимального управления шаг за шагом. Целевая функция выражает общий доход двух предприятий к концу 4-х лет работы в зависимости от выделяемых каждому предприятию средств 
 и
и  , соответственно, на начало каждого года – шага построения оптимального управления. Идея постепенной, пошаговой оптимизации системы
, соответственно, на начало каждого года – шага построения оптимального управления. Идея постепенной, пошаговой оптимизации системы 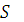 сформулирована Беллманом в виде общего принципа оптимальности: каково бы ни было состояние некоторой системы
сформулирована Беллманом в виде общего принципа оптимальности: каково бы ни было состояние некоторой системы  после
после 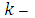 1 шагов, управление на
1 шагов, управление на 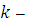 м шаге должно выбираться так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах с
м шаге должно выбираться так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах с  1
1 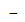 го до
го до  го включительно был максимальным (обеспечивал экстремум целевой функции).[1].
го включительно был максимальным (обеспечивал экстремум целевой функции).[1].
Принцип оптимальности выражающий суть метода динамического программирования, основан на марковском процессе перехода системы  из одного состояния в другое процессе с отсутствием последействия.
из одного состояния в другое процессе с отсутствием последействия.
Принцип оптимальности обладает свойством аудитивности, согласно которому максимальный доход после 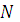 шагов правления слагается из доходов, получаемых на отдельных шагах управления:
шагов правления слагается из доходов, получаемых на отдельных шагах управления:
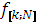 (
(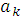 ) =
) = 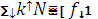 (
( ) +
) + 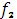 (
( )],
)],
где  и
и  средства выделенные предприятиями
средства выделенные предприятиями  и
и  в результате оптимального управления.
в результате оптимального управления.
В задаче рассматривается производственно экономическая управляемая система  – сумма средств
– сумма средств  , выделяемых двум предприятиям; её состояние перед каждым шагом управления характеризуется двумя параметрами: средствами
, выделяемых двум предприятиям; её состояние перед каждым шагом управления характеризуется двумя параметрами: средствами  каждого из предприятий.
каждого из предприятий.
В соответствии с принципом оптимальности планировать многошаговую операцию по распределению выделенных двум предприятиям средств необходимо не так, чтобы общий доход по окончании некоторого года был бы максимальным, а так, чтобы максимальной была сумма доходов по окончании некоторого года и всех оставшихся лет до конца 4-х летнего периода работы предприятий. Однако, существует единственный из всех шагов планирования распределения средств, на котором будет получен наибольший доход без учета всех последующих шагов. Очевидно, что таким шагом является последний шаг – планирование распределения средств между двумя предприятиями на начало их 4-го года работы. Поэтому процесс динамического программирования строится от конца к началу: от распределения средств на начало 4-го года переходим к распределению средств на начало 3-го года, затем – 2-го и, наконец, 1-го года работы предприятий.[2].
В математической форме принцип оптимальности Беллмана реализуется с помощью составления и поиска максимума целевой функции 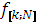 (
(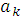 ):
):
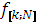 (
(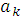 ) =
) = 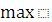 [
[  (
( ) +
) + 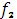 (
( ) +
) + 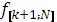 (
(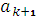 )]. (1)
)]. (1)
0≤  ≤
≤ 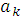
Выражение (1) называется основным функциональным (рекуррентным) уравнением динамического программирования, определяет полный доход, получаемый в результате распределения средств, начиная с величины 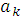 на
на 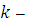 м этапе и заканчивая на
м этапе и заканчивая на  м этапе, и принимает вид:
м этапе, и принимает вид:
1) при  ,
,  (
( ) =
) = 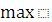 [
[ 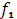 (
(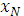 ) +
) + 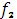 (
( )],
)], 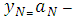
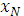 , (2)
, (2)
0≤ 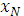 ≤
≤ 
2)при 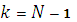 ,
,  , …,
, …,  (
(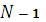 ),
), 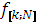 (
(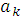 ) =
) = 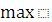 {
{  (
( ) +
) +
0≤  ≤
≤ 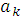
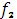 (
( )+
)+ 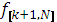 [
[ 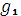 (
( )+
)+  (
( )
) 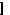 }, (3)
}, (3)
где 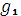 (
( )+
)+  (
( ) =
) = 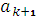
 остаток средств к концу
остаток средств к концу 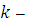 го года.
го года.
Выражение (1)  (3) позволяют определить средства
(3) позволяют определить средства  и
и  , выделяемые предприятиями
, выделяемые предприятиями  в результате оптимального управления их суммой
в результате оптимального управления их суммой  .
.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 487; Нарушение авторских прав?; Мы поможем в написании вашей работы!