
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 4. Математическое программирование 3 страница
|
|
|
|
Такие случаи «вырождения» могут возникать не только при составлении опорного плана перевозок, но и при его преобразовании, оптимизации.
В транспортной таблице всегда удобнее иметь 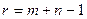 базисных (заполненных перевозками) клеток; в некоторым из них могут быть указаны нулевые перевозки. Клетки, в которые введены нулевые перевозки, называют фиктивно занятыми.
базисных (заполненных перевозками) клеток; в некоторым из них могут быть указаны нулевые перевозки. Клетки, в которые введены нулевые перевозки, называют фиктивно занятыми.
В анализируемый план, представленный таблицей 2, для устранения его вырожденности, необходимо ввести одну нулевую перевозку. Введем эту перевозку  в клетку (2, 2).
в клетку (2, 2).
4. Метод потенциалов
Исходный опорный план, построенный методом «северо-западного угла», обычно оказывается не оптимальным, так как для его определения не учитываются стоимости перевозок грузов от пунктов их отправления и пунктам назначения. Для получения оптимального плана могут быть использованы ряд методов, одним из которых является метод потенциалов.
Сущность методы потенциалов состоит в следующем. После того, как найден исходный план перевозок, каждому пункту отправления (или каждой строке транспортной таблицы) ставится в соответствие некоторое число 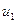 , называемой потенциалом этого пункта
, называемой потенциалом этого пункта  а каждому пункту назначения
а каждому пункту назначения  - некоторое число
- некоторое число 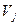 , называемое потенциалом пункта назначения
, называемое потенциалом пункта назначения 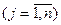 (или потенциалом столбца транспортной таблицы). Число
(или потенциалом столбца транспортной таблицы). Число 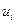 и
и 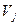 выбираются так, чтобы в каждой базисной (содержащей перевозку, в том числе и нулевые) клетки транспортной таблицы их суммы равнялась стоимости
выбираются так, чтобы в каждой базисной (содержащей перевозку, в том числе и нулевые) клетки транспортной таблицы их суммы равнялась стоимости 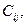 указанной в этой клетке:
указанной в этой клетке:
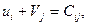
 (2.5)птоды потенциалов состоит в следущем ь использованы ряд методов, одним из которых является метод потенциалов.пунктов иху. _
(2.5)птоды потенциалов состоит в следущем ь использованы ряд методов, одним из которых является метод потенциалов.пунктов иху. _
Так как количество всех потенциалов 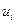 и
и 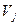 составляет
составляет  , а число базисных клеток с учетом фиктивно занятых равно
, а число базисных клеток с учетом фиктивно занятых равно 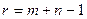 , то для определения числовых значений потенциалов необходимо решить систему (2.5) из
, то для определения числовых значений потенциалов необходимо решить систему (2.5) из 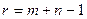 уравнений с
уравнений с  неизвестными. Следовательно, одному (любому) из неизвестных нужно придать произвольное значение (например, равное нулю), после чего остальные
неизвестными. Следовательно, одному (любому) из неизвестных нужно придать произвольное значение (например, равное нулю), после чего остальные  неизвестных определяются однозначно.
неизвестных определяются однозначно.
Доказано, что для того, чтобы опорный план был оптимальным, необходимо выполнение следующих условий:
а) для каждой базисной (заполненной перевозкой) клетки транспортной таблицы суммы потенциалов должна быть равна стоимости перевозки, указанной в этой клетке, т.е. должно выполняться равенство (2.5);
б) для каждой свободной (незанятой перевозкой) клетки транспортной таблицы сумма потенциалов должна быть меньше или равна стоимости перевозки, указанной в этой клетке, т.е. должно выполняться условие:

 (2.6)
(2.6)
Таким образом, для проверки плана перевозок на оптимальность необходимо найти потенциалы пунктов отправления и назначения грузов; решив систему (2.5), а затем проверить выполнение условий (2.6) для каждой из свободных (не содержащих перевозок) клеток транспортной таблицы. Для этого суммируются потенциалы строки и столбца этой таблицы, на пересечении которых стоит клетка, сумма сравнивается со стоимостью перевозки, указанной в этой клетке. Если для всех свободных клеток выполняется условие (2.6), то план перевозок является оптимальным. Если хотя бы для одной клетки сумма потенциалов превышает стоимость перевозки, указанной в этой клетке, т.е.  то план перевозок не является оптимальным и его необходимо улучшить, используя для этого соответствующие методы.
то план перевозок не является оптимальным и его необходимо улучшить, используя для этого соответствующие методы.
Методом потенциалов проанализируем план перевозок, представленный в транспортной таблице 2.
Как отмечено выше, указанный план является вырожденным, так как перевозками занято лишь 6 клеток таблицы, что не удовлетворяет условию 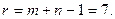 Для устранения вырожденности этого плана поместим нулевую перевозку
Для устранения вырожденности этого плана поместим нулевую перевозку  (она указана в таблице) в клетку (2, 2) и будем считать эту клетку занятой.
(она указана в таблице) в клетку (2, 2) и будем считать эту клетку занятой.
Для всех занятых клеток (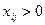 ) согласно (2.5) определяем потенциалы
) согласно (2.5) определяем потенциалы 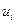 и
и 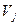 из системы:
из системы:
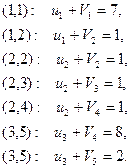
Здесь у каждого уравнения указана занятая перевозкой клетка, для которой составлено уравнение потенциалов.
Система потенциалов содержит 7 уравнений с 8 неизвестными. Следовательно, одно из неизвестных (любое) является свободным. Пологая 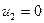 , находим:
, находим:

Теперь проверим выполнение условий оптимальности (2.6) для свободных (незанятых перевозками, 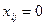 ) клеток транспортной таблицы 2. Имеем:
) клеток транспортной таблицы 2. Имеем:

Нетрудно видеть, что условие оптимальности (2.6) нарушено в клетках (2,1), (3,1), (3,2), (3,3). План перевозок, представленный в таблице 2, не является оптимальным и может быть улучшен.
5. Улучшение плана перевозок. Цикл пересчета
Если составленный план перевозок не является оптимальным (что устанавливается с помощью метода потенциалов), то он должен быть по возможности улучшен, т.е. изменен с целью уменьшения общей стоимости перевозки всех грузов. Такое улучшение плана может быть выполнено с использованием так называемых цикла пересчета и циклических перестановок грузов.
Циклом в транспортной таблице называют несколько клеток, соединенных замкнутой ломаной линией, звенья которой являются горизонтальные и вертикальные отрезки, параллельные строкам и столбцам таблицы.
Построение цикла начинают с какой-либо занятой клетки, затем переходят по строке (столбцу) к другой клетке, в которой делают поворот звена цикла под прямым углом и движутся вдоль столбца (строки) до следующей клетки и т.д. Клетки, в которых происходит поворот звена цикла, называют вершинами цикла. Циклы могут иметь различную конфигурацию и, в частности, быть самопересекающимися. Направление обхода цикла указывается стрелками. Если при построение цикла оказался возможен возврат в его начальную клетку, то цикл получен.
Циклические перестановки грузов заключаются в том, что некоторые перевозки перемещаются в том, что некоторые перевозки перемещаются из одной вершины цикла в другую без нарушения уже достигнутого (при составлении опорного плана) баланса по ее строкам и столбцам. Целью таких перестановок является уменьшение общей стоимости всех планируемых перевозок.
Будем отмечать знаком «+» те вершины цикла, в которых перевозки в результате циклической перестановки груза увеличиваются, а знаком «-» - те вершины, в которых перевозки уменьшаются.
Вершинам замкнутого цикла приписываются чередующиеся знаки. Свободным клеткам приписывается положительный знак. Циклы с отмеченными знаками «+» или «-» вершинами называют означенными.
Перенесением груза по означенному циклу называют увеличение перевозок, стоящих в положительных вершинах цикла на некоторое количество единиц груза при одновременном уменьшении перевозок, стоящих в отрицательных вершинах, на то же количество единиц груза. Очевидно, что при переносе любого числа единиц груза по циклу равновесие (баланс) между запасами и заявками не меняются: по-прежнему сумма перевозок в каждой строке транспортной таблицы остается равной запасам этой строки, а сумма перевозок в каждом столбце – заявке этого столбца, т.е. удовлетворяются равенства (2.1) и (2.2). Таким образом при любом циклическом переносе груза допустимый план транспортной задачи таковым и остается. Стоимость плана перевозок при этом в общем случае меняется – она может увеличиться или уменьшиться. Очевидно, для улучшения плана перевозок, приближения его к оптимальному, необходимо добиваться последнего.
Назовем ценой цикла изменение стоимости перевозок при перемещении одной единицы груза по означенному циклу. Очевидно, что цена цикла равна алгебраической сумме стоимости, указанных в вершинах цикла: стоимости, стоящие в положительных вершинах, берутся со знаком «+», а в отрицательных вершинах – со знаком «-».
Будем обозначать цену цикла через 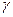 . При перемещении одной единицы груза по цикл, стоимость перевозок изменится на величину
. При перемещении одной единицы груза по цикл, стоимость перевозок изменится на величину 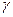 , а при перемещении по нему
, а при перемещении по нему 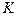 единиц груза – на величину
единиц груза – на величину  . Очевидно, что улучшение плана перевозок (уменьшение его стоимости) возможно при перемещении перевозок по таким циклом, цены которых отрицательны. При этом поскольку перевозки не могут быть отрицательными, то могут быть использованы только такие циклы, отрицательные вершины которых находятся в базисных (содержащих перевозки) клетках транспортной таблицы.
. Очевидно, что улучшение плана перевозок (уменьшение его стоимости) возможно при перемещении перевозок по таким циклом, цены которых отрицательны. При этом поскольку перевозки не могут быть отрицательными, то могут быть использованы только такие циклы, отрицательные вершины которых находятся в базисных (содержащих перевозки) клетках транспортной таблицы.
Таким образом метод последовательного улучшения плана перевозок заключается в том, что в транспортной таблице отыскиваются циклы с отрицательной ценой, по которым перемещаются циклы с отрицательной ценой, по которым перемещаются перевозки. План улучшается до тех пор, по циклов с отрицательной ценой в таблице не остается.
При улучшении плана с помощью циклических переносов грузов, как правило, при каждом цикле заполняют одну свободную клетку, а взамен освобождают одну свободную клетку, а взамен освобождают одну из базисных клеток. При этом общее число базисных клеток остается неизменным и равным 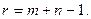
Доказано, что для любой свободной клетки транспортной таблицы всегда существует цикл (и притом единственный), одна из вершин которой лежит в этой свободной клетке, а все остальные – в базисных клетках. Если цена такого цикла, с плюсом в свободной клетке отрицательна, то план можно улучшить, перемещая перевозки по данному замкнутому циклу. При этом количество единиц груза 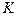 , которое можно переместить по циклу, равно минимальному значению перевозок, стоящих в отрицательных вершинах цикла. Большее число единиц груза переместить нельзя, т.к. при этом возникнут отрицательные перевозки.
, которое можно переместить по циклу, равно минимальному значению перевозок, стоящих в отрицательных вершинах цикла. Большее число единиц груза переместить нельзя, т.к. при этом возникнут отрицательные перевозки.
Если циклов с отрицательной ценой в транспортной таблице не осталось, это означает, что дальнейшее его улучшение невозможно, т.е. оптимальный план достигнут.
Выше изложенное позволяет сформулировать следующий алгоритм улучшения плана перевозок.
После того, как из системы (2,5) найдены потенциалы 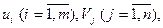 проверятся выполнение условий потенциальности (2.6) свободных клеток транспортной таблицы. Если критерии оптимальности (2ю5) и (2.6) выполнены, то составленный план является оптимальным (т.е. план перевозок оптимален, если он потенциален). Если же имеются свободные клетки, для которых условие потенциальности (2.6) не выполняется, то переходят к новому плану, производя пересчет по циклам с отрицательной ценой, соответствующим таким клеткам. Полученный таким образом новый план перевозок будет лучше предыдущего, т.к. затраты на его реализацию будут меньшими (поскольку при перемещении грузов по циклам с отрицательной ценой общие затраты на перевозки уменьшаются). Для нового плана вычисляются новые потенциалы
проверятся выполнение условий потенциальности (2.6) свободных клеток транспортной таблицы. Если критерии оптимальности (2ю5) и (2.6) выполнены, то составленный план является оптимальным (т.е. план перевозок оптимален, если он потенциален). Если же имеются свободные клетки, для которых условие потенциальности (2.6) не выполняется, то переходят к новому плану, производя пересчет по циклам с отрицательной ценой, соответствующим таким клеткам. Полученный таким образом новый план перевозок будет лучше предыдущего, т.к. затраты на его реализацию будут меньшими (поскольку при перемещении грузов по циклам с отрицательной ценой общие затраты на перевозки уменьшаются). Для нового плана вычисляются новые потенциалы 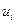 и
и 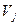 и снова проверяются условия его оптимальности. Процедура улучшения плана (уменьшения его стоимости) продолжается до тех пор, пока не будет получен оптимальный план.
и снова проверяются условия его оптимальности. Процедура улучшения плана (уменьшения его стоимости) продолжается до тех пор, пока не будет получен оптимальный план.
В соответствии с изложенным, перейдем к отысканию оптимального плана перевозок рассматриваемой нами задачи. С помощью метода потенциалов было установлено, что опорный план перевозок, представленный транспортной таблице 2, не является оптимальным, поскольку не выполняется условие оптимальности (2.6) для ее свободных клеток (2,1), (3,1), (3,2), (3,3). Стоимость указанного плана равна сумме произведений объемов перевозок, стоящих в заполненных клетках, на соответствующие стоимости перевозок, указанных в этих клетках, и составляет
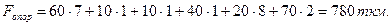
Найдем в транспортной таблице 2 цикл с отрицательной стоимостью, проходящий хотя бы через одну из указанных клеток, для которых не выполнено условие оптимальности. Можно видеть, что таким циклом, проходящим через клетку (3,1), является цикл с вершинами в клетках (1,1), (1,4), (3,4), (3,1), если стоимостям перевозок, указанным в этих клетках, приписать соответственно следующие знаки: -7, +4, -8, +5. При этом цена означенного цикла будет отрицательна и составит

Рассмотренный цикл и знаки его вершин указаны в транспортной таблице 2.
Количество единиц груза, которое можно переместить по этому циклу, равно минимальному значению перевозок, стоящие в отрицательных вершинах цикла, а именно:
Выполним перемещение 20 единиц груза по означенному циклу. В результате получим план перевозок, представленный в таблице 3:
По сравнению с исходным опорным планом стоимость полученного плана меньше на

и составляет

Легко видеть, что новый план перевозок является допустимым, т.к. выполнены балансные условия (2.1) и (2.2) соответственно по строкам и столбцам транспортной таблицы 3 и при этом план является опорным и невырожденным, поскольку число клеток, занятых фактическими перевозками, равно
Для невырожденного плана можно построить систему потенциалов и проверить его тем самым на оптимальность. С этой целью нужно снова построить систему потенциалов согласно (2.5) для каждой занятой клетки транспортной таблицы 3 и затем проверить выполнение условия оптимальности (2.6) для каждой свободной клетки.
Для потенциалов заполненных клеток транспортной таблицы 3 имеем:

Полагая 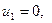 находим:
находим:

Теперь проверяем выполнение условия оптимальности (2.6) для каждой из свободных клеток. Имеем:

Условия оптимальности (2.6) выполнено для всех свободных клеток. Следовательно, план перевозок оптимален.
Ответ. План перевозок 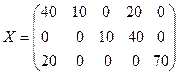 является оптимальным; его стоимость равна 660 ткм.
является оптимальным; его стоимость равна 660 ткм.
Задача 3
Рассмотрим задачу нелинейного выпуклого программирования 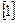 . На плоскости
. На плоскости 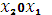 задана выпуклая область
задана выпуклая область  , определяемая системой неравенств
, определяемая системой неравенств
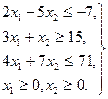 (3.1)
(3.1) 
Требуется в области  найти такую точку
найти такую точку 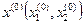 в которой функция
в которой функция
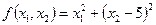 (3.2)
(3.2)
принимает минимальное значение. Решение выполнить графическим методом, написать функцию Лагранжа и найти ее седловую точку, используя графическое решение.
Анализ условия задачи
Основные теоретические сведения: Математическая модель задачи выпуклого программирования. Выпуклые и вогнутые функции. Теорема Куна  Таккера.
Таккера.
Общая задача выпуклого программирования относится к классу задач нелинейного программирования. Задача нелинейного программирования формулируется следующим образом 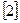 . В некоторой области
. В некоторой области  пространства
пространства  , определяемой системой
, определяемой системой 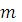 уравнений и неравенств
уравнений и неравенств
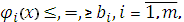 (3.3)
(3.3)
где 
задана функция  переменных
переменных
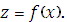 (3.4)
(3.4)
При этом либо 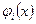 , либо
, либо 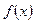 , либо и
, либо и 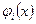 и
и 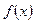 нелинейные функции.
нелинейные функции.
Найти такой вектор 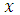 , при котором функция (3.4) принимает минимальное (максимальное) значение. Функция (3.4) называется целевой функцией.
, при котором функция (3.4) принимает минимальное (максимальное) значение. Функция (3.4) называется целевой функцией.
Универсального метода решения нелинейных задач не существует. Разработаны методы решения отдельных классов нелинейных задач, в частности, получившего широкое применение класса задач выпуклого программирования – задач, в которых функции 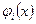 ,
, 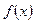 являются выпуклыми (вогнутыми), определенными в выпуклой области
являются выпуклыми (вогнутыми), определенными в выпуклой области  . Задача выпуклого программирования чаще всего ставится как задача поиска минимума выпуклой целевой функции
. Задача выпуклого программирования чаще всего ставится как задача поиска минимума выпуклой целевой функции  переменных
переменных
 ,
, 
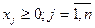 (3.5)
(3.5)
на выпуклом множестве  , определяемом системой ограничений
, определяемом системой ограничений

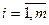 , (3.6)
, (3.6)
где 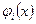
 выпуклые функции
выпуклые функции
Если ставится задача поиска максимума целевой функции, то в качестве целевой функции рассматривается вогнутая функция
 ,
, 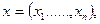
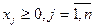 , (3.7)
, (3.7)
а выпуклое множество  определяется системой ограничений
определяется системой ограничений
 (3.8)
(3.8)
где 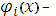 вогнутые функции.
вогнутые функции.
Определение: выпуклым множеством D точек 
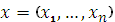 называется такое множество
называется такое множество  , которое вместе с любыми своими точками
, которое вместе с любыми своими точками 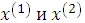 содержит и все точки
содержит и все точки  отрезка [
отрезка [  ], т.е. точки
], т.е. точки  , где
, где 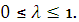
Точки  при этом являются выпуклыми линейными комбинациями точек
при этом являются выпуклыми линейными комбинациями точек 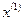 и
и  . Иногда выпуклая линейная комбинация точек
. Иногда выпуклая линейная комбинация точек 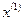 и
и  записывается в виде:
записывается в виде: 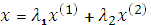 , где
, где 

Заметим, что любая прямая 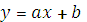 разделяет плоскость на две полуплоскости, каждая из которых представляет выпуклое множество точек. Пересечение любого числа выпуклых множеств является также выпуклым множеством
разделяет плоскость на две полуплоскости, каждая из которых представляет выпуклое множество точек. Пересечение любого числа выпуклых множеств является также выпуклым множеством 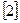 .
.
При выполнении

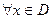 (3.9)
(3.9)
точка 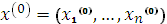 является точкой глобального минимума в области
является точкой глобального минимума в области  и вектор
и вектор 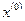 называется оптимальным планом,
называется оптимальным планом,
при
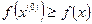
 (3.10)
(3.10)
точка 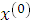 будет точкой глобального максимума.
будет точкой глобального максимума.
Функция 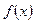 называется выпуклой в области
называется выпуклой в области 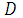 , если для
, если для  ,
, 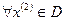 при
при  имеет место
имеет место
 (3.11)
(3.11)
и вогнутой, если
 (3.12)
(3.12)
Поскольку для 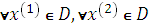 при
при  множеству
множеству  принадлежат также и точки
принадлежат также и точки  , что справедливо только тогда, когда множество
, что справедливо только тогда, когда множество  является выпуклым, то выпуклость и вогнутость функции
является выпуклым, то выпуклость и вогнутость функции 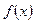 определяется только на выпуклом множестве
определяется только на выпуклом множестве  .
.
При строгом неравенстве (3.11) выпуклая функция называется строго выпуклой; аналогично, вогнутая функция называется строго вогнутой, если неравенство (3.12) строгое.
Определение выпуклой и вогнутой функции допускает геометрическую иллюстрацию в случаях двух переменных 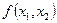 и одной переменной
и одной переменной 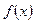 : выпуклая поверхность
: выпуклая поверхность  или график выпуклой функции
или график выпуклой функции  лежат ниже отрезка, соединяющего точки
лежат ниже отрезка, соединяющего точки 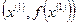 и
и 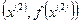 , а вогнутая поверхность или график вогнутой функции – выше. Для функции одной переменной
, а вогнутая поверхность или график вогнутой функции – выше. Для функции одной переменной 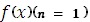 понятия выпуклости и вогнутости в области
понятия выпуклости и вогнутости в области 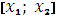 проиллюстрированы на рис. 1 и 2.
проиллюстрированы на рис. 1 и 2.
Рис.1 Определение выпуклой Рис.2 Определение вогнутой
функции  функции
функции 
Понятиям выпуклости и вогнутости функций характерна взаимообразность, если учесть, что выпуклой функции 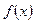 всегда соответствует вогнутая функция
всегда соответствует вогнутая функция 
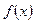 и наоборот. Взаимообразность выпуклости и вогнутости позволяет задачу минимизации целевой функции заменить задачей максимизации и наоборот. Поясним это утверждение на примере функции одной переменной
и наоборот. Взаимообразность выпуклости и вогнутости позволяет задачу минимизации целевой функции заменить задачей максимизации и наоборот. Поясним это утверждение на примере функции одной переменной  . Предположим, что точка
. Предположим, что точка  является точкой минимума функции
является точкой минимума функции 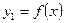 . Тогда в этой же точке функция
. Тогда в этой же точке функция  имеет максимум, поскольку графики функций
имеет максимум, поскольку графики функций 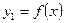 и
и  симметричны относительно оси абсцисс (рис. 3)
симметричны относительно оси абсцисс (рис. 3)
Рис.3 Переход от задачи минимизации функции к задаче
максимизации функции  .
.
В результате получаем
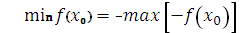 . (3.13)
. (3.13)
Подобный переход имеет место и для функции нескольких переменных. 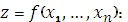
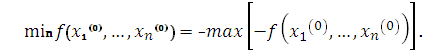 (3.14)
(3.14)
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 479; Нарушение авторских прав?; Мы поможем в написании вашей работы!