
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Вычислительный алгоритм динамического программирования процесса поиска максимального дохода двух предприятий предусматривает следующие операции
|
|
|
|
Вычислительный алгоритм динамического программирования процесса поиска максимального дохода двух предприятий предусматривает следующие операции.
1. По условию задачи период, на который выделено  = 1000 единиц денежных средств для получения максимального дохода, равен 4
= 1000 единиц денежных средств для получения максимального дохода, равен 4  м годам. Разобьём его на 4 этапа распределения выделенных средств, имеем
м годам. Разобьём его на 4 этапа распределения выделенных средств, имеем 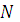 = 4,
= 4,  = 1, 2, 3, 4.
= 1, 2, 3, 4.
2. Определение максимального дохода начинаем с 4  го этапа, в начале которого необходимо распределить остаток средств от 3
го этапа, в начале которого необходимо распределить остаток средств от 3 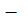 го этапа:
го этапа: 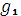 (
(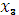 ) +
) +  (
(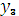 ) =
) = 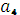 . Чтобы найти средства
. Чтобы найти средства 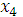 и
и 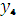 , выделяемые на 4м этапе предприятиями
, выделяемые на 4м этапе предприятиями  , и при этом получить максимальный доход
, и при этом получить максимальный доход 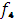 (
(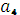 ), составим функциональное уравнение (2):
), составим функциональное уравнение (2):
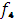 (
(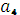 ) =
) = 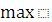 [
[ 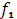 (
(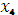 )+
)+ 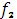 (
(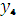 )] =
)] = 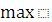 [
[ 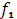 (
(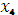 )+
)+ 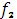 (
(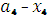 )] =
)] = 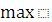 [5
[5 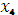 +4(
+4(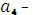
0≤ 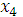 ≤
≤ 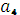 0≤
0≤ 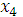 ≤
≤ 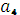 0≤
0≤ 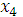 ≤
≤ 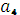
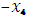 )] =
)] = 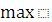 (
(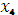 +4
+4 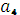 ) = 5
) = 5 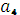 .
.
0≤ 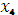 ≤
≤ 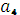
Получили линейную относительно 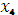 функцию
функцию 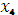 + 4
+ 4 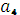 , которая на отрезке [0;
, которая на отрезке [0; 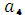 ] принимает максимальное значение
] принимает максимальное значение 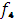 (
(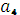 ) = 5
) = 5 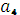 при
при 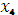 =
= 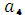 .
.
Таким образом, максимальный доход на 4  м этапе, равный величине
м этапе, равный величине 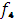 (
(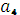 ) = 5
) = 5 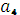 , имеет место, если все выделяемые на 4
, имеет место, если все выделяемые на 4  м этапе средства
м этапе средства 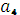 вложить в предприятие
вложить в предприятие  , ничего не оставляя предприятию
, ничего не оставляя предприятию  :
: 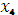 =
= 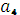 ,
, 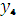 = 0. Это будет оптимальное распределение средств
= 0. Это будет оптимальное распределение средств 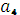 на начало 4 – го года.
на начало 4 – го года.
Далее, используя функциональное уравнение (3), последовательно определяем оптимальное распределение средств на 3, 2 и 1 –м этапах.
3. Запишем функциональное уравнение (3) для 3 – го этапа, определяющее максимальный доход при оптимальном распределении средств на 3 – м и 4 – м этапах:
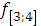 (
(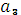 ) =
) = 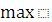 [
[ 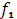 (
(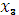 ) +
) + 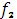 (
(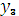 ) +
) + 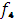 (
(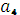 )]. (4)
)]. (4)
0≤ 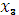 ≤
≤ 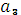
Здесь 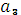 =
=  +
+ 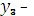 сумма средств, распределяемых между предприятиями
сумма средств, распределяемых между предприятиями  и
и 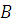 на 3
на 3  м этапе,
м этапе, 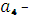 остаток от этих средств к концу 3
остаток от этих средств к концу 3 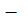 го года, который перейдет на начало 4
го года, который перейдет на начало 4 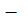 го года в качестве средств, подлежащих распределению на 4
го года в качестве средств, подлежащих распределению на 4 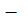 м этаже.
м этаже.
Находим 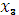 и
и 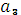
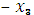 средства, выделяемые предприятиям
средства, выделяемые предприятиям  и
и  на 3
на 3 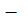 ем этапе (оптимальное управление на 3-м этапе), обеспечивающие прибыль
ем этапе (оптимальное управление на 3-м этапе), обеспечивающие прибыль 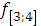 (
(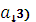 . Подставляя в (4) выражения для
. Подставляя в (4) выражения для 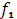 (
(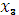 ),
), 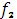 (
(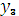 ),
), 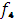 (
(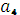 ), получим:
), получим:
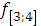 (
(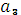 ) =
) = 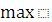 {5
{5 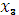 +4(
+4(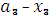 ) + 5[0,3
) + 5[0,3 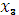 +0,5(
+0,5(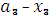 )
) 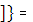
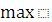 6,5
6,5 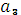 = 6,5
= 6,5 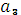 .
.
0≤ 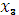 ≤
≤  0≤
0≤ 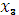
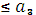 Видно, что максимальный доход
Видно, что максимальный доход 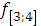 (
(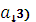 =
= 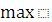 6,5
6,5 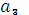 3
3  го и 4 го
го и 4 го
0 
 ≤
≤ 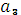
этапов не зависит от средств 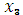 , поэтому средства
, поэтому средства 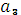 выделяемые предприятиям
выделяемые предприятиям  и
и  на 3
на 3  м этаже, можно распределить между предприятиями
м этаже, можно распределить между предприятиями  и
и  любым способом в пределах суммы
любым способом в пределах суммы  ,
,
4. Запишем для 2  го этапа функциональное уравнение (3), определяющее максимальный доход, получаемый от оптимального управления распределением средств на 2
го этапа функциональное уравнение (3), определяющее максимальный доход, получаемый от оптимального управления распределением средств на 2  м, 3
м, 3  м и 4
м и 4  м этапах:
м этапах:
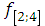 (
(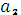 ) =
) = 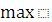 [
[ 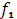 (
( ) +
) +  (
(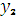 ) +
) +  (
(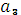 )] =
)] = 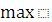 {5
{5  +4(
+4(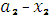 )+ 6,5[0,3
)+ 6,5[0,3  +
+
0≤  ≤
≤ 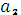 0≤
0≤  ≤
≤ 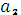
+0,5(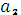 +
+  )]} =
)]} = 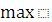 (7,25
(7,25 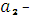 0,3
0,3  ) = 7,25
) = 7,25 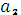 при
при  = 0,
= 0, 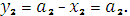
0≤  ≤
≤ 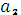
Таким образом, для получения максимального дохода при совместной работе двух предприятий на 2 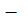 м, 3
м, 3  м и 4
м и 4  м этапах необходимо на 2
м этапах необходимо на 2  м этапе выполнить оптимальное управление: все оставшиеся после 1
м этапе выполнить оптимальное управление: все оставшиеся после 1  го этапа средства
го этапа средства 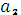 вложить в предприятие
вложить в предприятие  .
.
5. Наконец, составляем функциональное уравнение (3) для 1  го этапа и находим оптимальное управление на 1
го этапа и находим оптимальное управление на 1  м этапе и соответствующий ему максимальный доход при совместной работе предприятий
м этапе и соответствующий ему максимальный доход при совместной работе предприятий  и
и  на протяжении всего планируемого периода 4
на протяжении всего планируемого периода 4  го,3
го,3  го, 2
го, 2  го и 1
го и 1  го года:
го года:
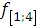 (
(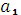 =
= 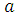 ) =
) = 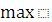 [
[ 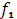 (
( ) +
) + 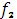 (
(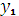 ) +
) + 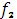 (
(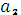 )] =
)] = 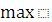 {5
{5  +4(
+4(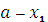 ) +
) +
0≤  ≤
≤  0≤
0≤  ≤
≤ 
+7,25[0,3  +0,5(
+0,5(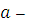
 )]} =
)]} = 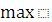 (7,625
(7,625 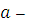 0,45
0,45  )= 7,625
)= 7,625 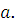 (5)
(5)
0≤  ≤
≤ 
Решение уравнения (5) основано на выборе оптимального управления: исследуемая функция достигает максимального значения на отрезке [0;  ] при
] при 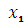 = 0.
= 0.
Таким образом, на 1  м этапе оптимальное управление будет заключаться в том, чтобы все выделенные средства на работу предприятий
м этапе оптимальное управление будет заключаться в том, чтобы все выделенные средства на работу предприятий  и
и  на протяжении 4
на протяжении 4  х лет на первом году их работы вложить только в предприятие
х лет на первом году их работы вложить только в предприятие  :
: 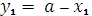 =
= 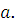 Остаток от этих средств к концу 1
Остаток от этих средств к концу 1  го года в дальнейшем использовать для перераспределения между предприятиями
го года в дальнейшем использовать для перераспределения между предприятиями  и
и  в начале 2
в начале 2  го года.
го года.
Выводы
1. Оптимальное управление процесс распределения средств на основе принципа оптимальности Беллмана состоит в следующем. На первом этапе все выделенные предприятиям  и
и  средства выгодно вложить только в предприятие
средства выгодно вложить только в предприятие  :
:  =
=  = 1000. К концу 1
= 1000. К концу 1  го года работы остаток средств
го года работы остаток средств  (
(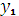 ) = 0,5
) = 0,5 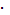
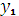 = 500 вложить также только в предприятие
= 500 вложить также только в предприятие  . Полученный остаток
. Полученный остаток  (
(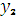 ) = 0,5
) = 0,5 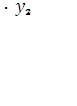 = =250 произвольно распределить между предприятиями
= =250 произвольно распределить между предприятиями  и
и  в начале 3
в начале 3  го года. Остаток средств
го года. Остаток средств 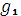 (
(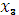 ) +
) +  (
(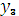 ) = 0,3
) = 0,3 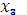 + 0,5
+ 0,5 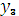 к концу 3
к концу 3  го года, который перейдет на 4
го года, который перейдет на 4  й год, отдать 1
й год, отдать 1  му предприятию:
му предприятию: 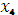 = 0,3
= 0,3 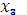 + 0,5
+ 0,5 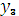 .
.
2. Максимальный доход двух предприятий  и
и  за 4
за 4 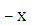 летний период их работы составит:
летний период их работы составит:
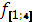 (
( ) =
) = 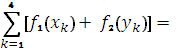 7,625
7,625 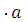 = 7,625
= 7,625 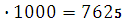
3. Результаты оптимального управления процессом распределения средств  =
=  +
+  между предприятиями
между предприятиями  и
и  представлены в таблице.
представлены в таблице.
Таблица
Оптимальное распределение средств между предприятиями  и
и 
Этапы,

| Распределение средства на начало  –го этапа –го этапа
| Оптимальное уравнение | Доход по годам | |||

|
 = = 
|
Предпр. 
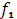 ( ( )=5 )=5 
|
Предпр. 
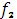 ( ( )=4 )=4 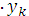
| |||
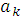 = = 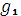 ( ( )+ )+  ( ( ) )
| ||||||
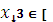 0;250] 0;250]
| 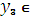 {250 {250
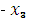 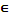
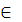 [0;250]} [0;250]}
| 0÷1250 | 1000÷0 | |||
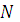 =4 =4
| 125÷75 | 125÷75 | 625÷375 |
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 410; Нарушение авторских прав?; Мы поможем в написании вашей работы!