
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 4. Математическое программирование 1 страница
|
|
|
|
Контрольная работа №5
По вопросам приобретения
книг издательства «КАРО»
обращайтесь в наши представительства:
Оптовая торговля:
в Санкт-Петербурге: ул. Бронницкая, 44 в Москве: ул. Краснобогатырская, 31
тел./факс: (812) 575-94-39,320-84-79 тел./факс: (495) 964-02-10,964-08-46
e-mail: karo@peterstar.ru e-mail: moscow@karo.net.ru;
Розничная торговля: www.karo.spb.ru
в Санкт-Петербурге: в Москве:
Торговая фирма «Санкт-Петербургский «Библио-Глобус» Торговый дом
Дом Книги», библиографический отдел Тел.: (495) 928-35-67,924-46-80
Тел.: (812) 314-58-88,570-65-46 «Московский дом книги»
«Азбука», пр.Обуховской обороны, -j-gjj. /495) 789-35-91
т 103/»i ->\ «-7 «««Молодая гвардия» Дом книги
1ел.. (nil) 36/-S6-63 Тел - (495) 238-50-01, 238-26-86
Магазин в помещении ЛОИРО, „ „,,
„ „ „,. Торговый дом книги «Москва»
Чкаловскии пр. 25А F ".
Сеть книжных магазинов «Буквоед» 1ел" '^Э'' ^-У-ьч-ы
«Дом книги» Медведково
в Великом Новгороде: Тел- (495) 476-00-23
Книжный магазин «Прометей» «Дом книги на Ладожской»
Тел.: (8162) 77-30-21 Тел.: (495) 267-03-02
Угебное издание Юрий Борисович Голицынский Нина Антоновна Голицынская
ГРАММАТИКА
Сборник упражнений
Издание пятое,
исправленное и дополненное
Н. А. Голицынской
Лицензия ЛР № 065644
Подписано в печать 14.07.2006.Формат 84xl08V32-
Гарнитура «Школьная». Бумага газетная. Печать офсетная.
Усл. печ. л. 28,6. Доп.тираж 25 000. Заказ № 1895.
Издательство «КАРО» 195279, Санкт-Петербург, шоссе Революции, 88
Отпечатано по технологии CtP в ОАО «Печатный двор» им. А. М. Горького 197110, Санкт-Петербург, Чкаловскии пр., 15.
Задача 1
1. Задача линейного программирования
Рассмотрим следующую Задачи.
Для производства двух видов изделия А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется 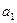 часов, оборудование второго типа –
часов, оборудование второго типа – 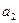 часов, оборудование третьего типа –
часов, оборудование третьего типа –  часов. Для производства единицы изделия В оборудование первого типа используется
часов. Для производства единицы изделия В оборудование первого типа используется  часов, оборудование второго типа –
часов, оборудование второго типа –  часов, оборудование третьего типа –
часов, оборудование третьего типа –  часов. На изготовление всех изделий предприятие может использовать оборудование первого типа не более, чем
часов. На изготовление всех изделий предприятие может использовать оборудование первого типа не более, чем  часов, второго типа – не более, чем
часов, второго типа – не более, чем  часов, третьего типа – не более, чем
часов, третьего типа – не более, чем  часов. Прибыль от реализации готового изделия А составляет
часов. Прибыль от реализации готового изделия А составляет  денежных единиц, а изделия В -
денежных единиц, а изделия В -  денежных единиц.
денежных единиц.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Решить задачу симплексным методом путем преобразования симплекс-таблиц. Дать геометрическое истолкование задачи, используя для этого ее формулировку с ограничениями задачи.
Составим математическую модель задачи.
Обозначим  и
и  количество изделий видов А и В соответственно, производимых предприятием.
количество изделий видов А и В соответственно, производимых предприятием.
Неизвестные значения  и
и  , очевидно, должны удовлетворять следующим условиям.
, очевидно, должны удовлетворять следующим условиям.
Так как на производство единицы изделия вида А используется 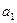 часов оборудование первого типа, а на производство единицы изделия вида В используется
часов оборудование первого типа, а на производство единицы изделия вида В используется  часов оборудование первого типа и общее число часов использования оборудования первого типа не должно превышать
часов оборудование первого типа и общее число часов использования оборудования первого типа не должно превышать  часов, то суммарное время производства
часов, то суммарное время производства  изделий вида А и
изделий вида А и  изделий всегда В.
изделий всегда В.
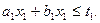
Аналогично из условия ограниченности времени использования оборудования второго и третьего типов устанавливаем, что

Если прибыль предприятия от одного изделия А составляет  денежных единиц, а от реализации одного изделия В -
денежных единиц, а от реализации одного изделия В -  единиц, то прибыль предприятия от реализации
единиц, то прибыль предприятия от реализации  единиц изделий А и
единиц изделий А и  - изделий В составит
- изделий В составит

Эта прибыль должна быть максимизирована за счет выбора количества производимых изделий вида А и В.
Дополнительно отметим, что по смыслу задачи 
Таким образом, постановка задачи состоит в следующем:
Найти неотрицательные решения
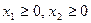 (1.1)
(1.1)
системы неравенств-ограничений
 (1.2)
(1.2)
при которых функция
 (1.3)
(1.3)
достигает максимума.
Задачи, подобные сформулированной, называются задачами линейного программирования.
Линейное программирование – область математики, в которой изучаются методы отыскания экстремальных значений линейной функции нескольких переменных при условии, что последние удовлетворяют конечному числу линейных неравенств или уравнений.
Функция, для которой находится ее экстремальное (наибольшее или наименьшее значение), называют целевой функцией (или функцией цели), а системы неравенств или уравнений, которым должны удовлетворять переменные целевой функции, называют системами ограничений.
В сформулированной задаче целевой функцией является функция (1.3), а системой ограничений – система неравенств (1.2).
Любое решение системы ограничений называется допустимым решением задачи линейного программирования.
Допустимое решение, при котором целевая функция достигает экстремального (максимального или минимального) значения, называется оптимальным решением.
Решение задачи линейного программирования заключается в отыскании оптимального решения, если оно существует.
Все задачи линейного программирования можно разбить на два вида. Задачи, в которых требуется максимизировать целевую функцию, называют задачами максимизации. Задачи, в которых требуется минимизировать целевую функцию, - задачами минимизации.
Учитывая, что  любую задачу минимизации и наоборот.
любую задачу минимизации и наоборот.
2. Графический метод решения задачи линейного программирования
Решение задачи линейного программирования с двумя переменными может быть выполнено графическим методом.
Для определенности рассмотрим задачу (1.1) – (1.3) при следующих значениях исходных данных:

При этом задача (1.1) – (1.3) принимает вид:
 (1.4)
(1.4)
 (1.5)
(1.5)
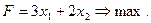 (1.6)
(1.6)
Каждое из неравенств задачи определяет некоторую полуплоскость вместе с граничной прямой, уравнение которой получается заменой знака неравенства на знак равенства. Общая часть этих полуплоскостей определяет область (многоугольник) допустимых решений задачи.
Найдем графически решения всех неравенств задачи.
Неравенствам (1.4) соответствуют полуплоскости, расположенные над осью абсцисс и справа от оси ординат. Для наглядности на чертеже отметим это штриховкой, которую нанесем над осью абсцисс и справа от оси ординат (рис. 3).
Найдем графически решение первого неравенства системы (1.5).

Для этого в системе координат  изобразим граничную прямую
изобразим граничную прямую

Для этого найдем точки, в которых эта прямая пересекает оси координат. В точке пересечения с осью 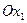 имеем
имеем 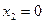 и поэтому
и поэтому  следовательно,
следовательно, 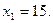 В точке пересечения рассматриваемой прямой с осью
В точке пересечения рассматриваемой прямой с осью  имеем
имеем  поэтому
поэтому  Таким образом, прямая
Таким образом, прямая  проходит через точки Е (0; 30) и D (15; 0). Построим эту прямую (рис. 3).
проходит через точки Е (0; 30) и D (15; 0). Построим эту прямую (рис. 3).
Теперь установим, какую полуплоскость определяет соответствующее неравенство  Для этого возьмем какую-либо (произвольную) точку, например О (0; 0) и ее координаты в рассматриваемое неравенство:
Для этого возьмем какую-либо (произвольную) точку, например О (0; 0) и ее координаты в рассматриваемое неравенство:  или
или  . Видим, что координаты точки О (0; 0) удовлетворяют неравенству. Следовательно, неравенству
. Видим, что координаты точки О (0; 0) удовлетворяют неравенству. Следовательно, неравенству  соответствует полуплоскость, в которой находится точка О (0; 0). Полуплоскость, определяемую неравенством
соответствует полуплоскость, в которой находится точка О (0; 0). Полуплоскость, определяемую неравенством  (рис. 3).
(рис. 3).
Аналогичным образом находятся полуплоскости, определяемы двумя другими неравенствами системы (1.5):

Пересечение всех найденных полуплоскостей, соответствующих всем неравенствам-ограничениям (1.4) и (1.5) задачи, определяет многоугольник 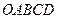 , являющийся областью допустимых решений задачи (рис. 3).
, являющийся областью допустимых решений задачи (рис. 3).
Теперь из всех допустимых решений нужно выбрать оптимальное решение, которое обеспечивает предприятию наибольшую прибыль, то есть максимум целевой функции (1.6).
Если целевой функции придать определенное числовое значение, то ее также можно представить графически. Положим, например, 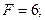 тогда получим уравнение прямой
тогда получим уравнение прямой  Точки, лежащие на этой прямой, соответствуют плану производства изделий А и В, при котором прибыль предприятия от реализации этих изделий составит
Точки, лежащие на этой прямой, соответствуют плану производства изделий А и В, при котором прибыль предприятия от реализации этих изделий составит 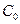 денежных единиц.
денежных единиц.
Линия, во всех точках которой целевая функция принимает одно и то же значение, называется линией уровня этой функции.
Уравнение  определяет на плоскости
определяет на плоскости  семейство параллельных прямых (линий уровня целевой функции), каждая из которых отвечает определенному значению целевой функции (1.6) рассматриваемой задачи. Вектор
семейство параллельных прямых (линий уровня целевой функции), каждая из которых отвечает определенному значению целевой функции (1.6) рассматриваемой задачи. Вектор  (вектор градиента) перпендикулярный (при условии, что масштабы по осям координат одинаковы) к этим прямым указывает направление наискорейшего возрастания целевой функции
(вектор градиента) перпендикулярный (при условии, что масштабы по осям координат одинаковы) к этим прямым указывает направление наискорейшего возрастания целевой функции  задачи. Если в одной и той же системе координат изображены область допустимых решений системы (1.4) – (1.5) и семейство прямых
задачи. Если в одной и той же системе координат изображены область допустимых решений системы (1.4) – (1.5) и семейство прямых  то задача определения точки максимума целевой функции F сводится к нахождению в допустимой области точки, через которую проходит прямая семейства
то задача определения точки максимума целевой функции F сводится к нахождению в допустимой области точки, через которую проходит прямая семейства 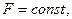 отвечающая наибольшему значению целевой функции (1.6).
отвечающая наибольшему значению целевой функции (1.6).
В соответствии с изложенным, построим вектор  и перпендикулярно к нему построим одну из прямых семейства
и перпендикулярно к нему построим одну из прямых семейства 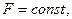 например,
например, 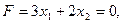 проходящую через начало системы координат. Построенную прямую
проходящую через начало системы координат. Построенную прямую 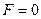 будем перемещать параллельно самой себе в направлении вектора
будем перемещать параллельно самой себе в направлении вектора  При этом легко видеть, что максимальное значение целевой функции на область допустимых решений задачи будет достигнуто в угловой точке С. Координаты точки С можно определить либо непосредственно по чертежу, либо решив совместно уравнения прямых пересекающихся в этой точке.
При этом легко видеть, что максимальное значение целевой функции на область допустимых решений задачи будет достигнуто в угловой точке С. Координаты точки С можно определить либо непосредственно по чертежу, либо решив совместно уравнения прямых пересекающихся в этой точке.
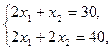
Таким образом, точкой, в которой достигается оптимальное решение задачи, является точка С(10; 10). При этом максимальное значение целевой функции равно
 денежных единиц.
денежных единиц.

Отметим дополнительно некоторые свойства решения задачи линейного программирования, легко устанавливаемые с помощью графического метода.
1. Если оптимальное решение задачи существует, то оно достигается по крайней мере в одной из вершин области (многоугольника) допустимых решений.
2. В случае, когда линии уровня целевой функции параллельны одной из сторон многоугольника допустимых решений, задача линейного программирования имеет бесконечное множество решений, которые достигаются в любой точке указанной стороны многоугольника решений.
3. В случае неограниченной области допустимых решений задача линейного программирования может не иметь решения, если в этой области целевая функция не ограничена сверху (снизу).
4. Для того, чтобы найти оптимальное решение задачи линейного программирования в случае ограниченной области допустимых решений, можно вычислить значения целевой функции задачи во всех вершинах многоугольника решений. Оптимальное решение соответствует координатам той вершины, в которой целевая функция достигает требуемого в задаче экстремуму (минимального или максимального).
3. Симплекс-метод решения задачи линейного программирования
Графический метод решения задач линейного программирования применим к весьма узкому классу задач: эффективно им можно решать задачи, содержащие не более двух переменных. В общем случае (при произвольном числе переменных) применяются универсальные вычислительные методы. Одним из них является симплекс-метод (называемый также методом последовательного улучшения плана).
Проиллюстрируем этот метод на примере уже рассмотренной задачи (1.4) – (1.6).
Алгоритм применения симплекс-метода сформулирован применительно к постановке задачи линейного программирования в так называемой канонической форме. Она заключается в следующем.
Условия-ограничения задача необходимо записать в виде:
 (1.7)
(1.7)
 (1.8)
(1.8)
Имеется решение задачи минимизации целевой функции:
 (1.9)
(1.9)
Требуемый в задаче (1.4) – (1.6) максимум целевой функции (1.6)

будет равен минимуму функции 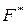 (1.9), взятому с противоположным знаком. Оба указанных экстремума достигаются при одних и тех же значения переменных.
(1.9), взятому с противоположным знаком. Оба указанных экстремума достигаются при одних и тех же значения переменных.
Для решения задачи симплекс-методом вводятся дополнительные неотрицательные переменных  по формулам:
по формулам:
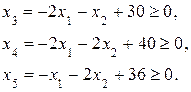 (1.10)
(1.10)
значения дополнительных переменных  равны соответствующим выражениям в левых частях неравенств (1.8). Очевидно, что согласно (1.7) и (1.10) имеет место условие неотрицательности всех переменных задачи:
равны соответствующим выражениям в левых частях неравенств (1.8). Очевидно, что согласно (1.7) и (1.10) имеет место условие неотрицательности всех переменных задачи: 
В неравенствах (1.10), связывающих значения исходных переменных задачи 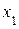 и
и 
 и дополнительных переменных
и дополнительных переменных  переменные
переменные 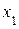 и
и  называются свободными, а переменные
называются свободными, а переменные  - базисными. Указанное разделение переменных на свободные и базисные, вообще говоря, условно: любое свободное переменное может быть переведено в базисные и наоборот – любое базисное переменное может быть переведено в свободные. Такие преобразования имеют существенное значение в симплекс-методе решения задач линейного программирования.
- базисными. Указанное разделение переменных на свободные и базисные, вообще говоря, условно: любое свободное переменное может быть переведено в базисные и наоборот – любое базисное переменное может быть переведено в свободные. Такие преобразования имеют существенное значение в симплекс-методе решения задач линейного программирования.
4. Симплекс-таблица
Условия задачи (1.7) – (1.9) оформим в виде так называемой симплекс-таблицы:
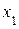
| 
| св. ул. | |
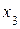
| -2 | -1 | |

| -2 | -2 | |

| -1 | -2 | |
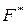
| -3 | -2 |
(1.11)
В заглавной строке симплекс-таблицы указываются исходные свободные переменные задачи 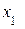 и
и  В левом столбце указываются исходные базисные переменные
В левом столбце указываются исходные базисные переменные  В правом столбце указываются свободные члены системы неравенств (1.8). В нижней строке указываются коэффициенты целевой функции, включая её свободный член
В правом столбце указываются свободные члены системы неравенств (1.8). В нижней строке указываются коэффициенты целевой функции, включая её свободный член 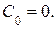 В остальных клетках симплекс-таблицы записывают коэффициенты, с которыми свободные переменные
В остальных клетках симплекс-таблицы записывают коэффициенты, с которыми свободные переменные 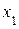 и
и  входят в выражения базисных переменных.
входят в выражения базисных переменных.
Введем ряд определений, необходимых для дальнейшего изложения симплекс-метода решения задачи линейного программирования.
Симплекс-таблицу, в которой свободные члены неотрицательны, называют полуприведенной. Записанная выше исходная симплекс-таблица рассматриваемой задачи является полуприведенной.
Симплекс-таблицу, в которой все свободные члены и все коэффициенты целевой функции (кроме, может быть, свободного члена 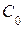 ) неотрицательны, называют приведенной.
) неотрицательны, называют приведенной.
Допустимое решение задачи линейного программирования, в котором все свободные переменные равны нулю, а вес базисные переменные неотрицательны, называют опорным решением задачи.
В теории симплекс-метода доказаны следующие теоремы.
Теорема 1. Для того, чтобы симплекс-таблице соответствовало опорное решение, необходимо и достаточно, чтобы симплекс-таблица была полуприведенной.
Теорема 2. Приведенному состоянию симплекс-таблицы соответствует оптимальное решение задачи линейного программирования.
Теорема 3. Если оптимальное решение задачи линейного программирования существует, то оно является одним из опорных решений задачи.
Согласно изложенному, решение задачи линейного программирования состоит из двух этапов:
1. отыскание опорных решений,
2. среди опорных решений отыскание оптимального.
Для осуществления первого этапа в соответствии с теоремой 1 требуется привести симплекс-таблицу задачи в полуприведенное состояние. Для выполнения второго этапа требуется перевести симплекс-таблицу из полуприведенного в приведенное состояние, которому согласно теореме 2 соответствует искомое оптимальное решение.
5. Симплекс-преобразования
Процедура преобразования исходной симплекс-таблицы задачи к приведенному состоянию может выполнена по определенной системе правил (алгоритму), основанной на «переразрешении» системы неравенств (1.10) относительно свободных и базисных переменных задачи. Существо такого переразрешения состоит в том, что соответствующим образом выбранная свободная переменная переводится в базисные, а взамен её в свободные переменные переводится некоторая базисная переменная. Например, свободная переменная 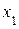 переводится в базисные, а базисная переменная
переводится в базисные, а базисная переменная 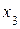 переводится в свободные. Указанную операцию будем обозначать символически
переводится в свободные. Указанную операцию будем обозначать символически 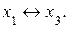
В результате указанных замен будут меняться коэффициенты в системе неравенств (1.10) и в выражении целевой функции (1.9), т.е. будет меняться симплекс-таблица задачи, её состояние. Это новое состояние симплекс-таблицы необходимо получить, что можно сделать по следующему алгоритму.
Предположим, что производится перевод свободного переменного  в базисные, а базисной переменной
в базисные, а базисной переменной  - в свободные, т.е. выполняется замена
- в свободные, т.е. выполняется замена  Выделим в симплекс-таблице коэффициент
Выделим в симплекс-таблице коэффициент 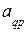 , с которым свободная переменная
, с которым свободная переменная  входит в выражение базисной переменной
входит в выражение базисной переменной  . Этот коэффициент называют разрешающим элементом
. Этот коэффициент называют разрешающим элементом  и для удобства выделяют в симплекс-таблице, например, кружком. Будем предполагать, что разрешающий элемент отличен от нуля. Выделим строку и столбец симплекс-таблицы, в которых стоит разрешающий элемент. Эту строку и этот столбец будем называть разрешающей строкой и разрешающим столбцом.
и для удобства выделяют в симплекс-таблице, например, кружком. Будем предполагать, что разрешающий элемент отличен от нуля. Выделим строку и столбец симплекс-таблицы, в которых стоит разрешающий элемент. Эту строку и этот столбец будем называть разрешающей строкой и разрешающим столбцом.
Алгоритм преобразования элементов симплекс-таблицы при выполнении замены 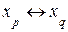 состоит в следующем.
состоит в следующем.
1. Разрешающий элемент заменяется его обратной величиной и записывается в соответствующему ему клетку новой симплекс-таблицы.
2. Все остальные элементы разрешающего столбца делятся на разрешающий элемент и записываются в соответствующие клетки симплекс-таблицы.
3. Все элементы разрешающей строки (кроме  ) меняют знак и делятся на разрешающий элемент; результаты записываются в соответствующие клетки новой симплекс-таблицы.
) меняют знак и делятся на разрешающий элемент; результаты записываются в соответствующие клетки новой симплекс-таблицы.
4. Все остальные элементы новой симплекс-таблицы, не принадлежащие ни разрешающей строке, ни разрешаемому столбцу, вычисляются по так называемому «правилу прямоугольника», состоящему в следующем.
Выделим в исходной таблице разрешающие строку и столбец и рассмотрим «прямоугольник», в двух противоположных вершинах которого находятся разрешающий элемент симплекс-таблицы а. Элементы симплекс-таблицы, расположенные в двух противоположных вершинах выделенного прямоугольника, обозначим (для простоты) через b и С. Новое значение  элемента симплекс-таблицы вычисляется по формуле:
элемента симплекс-таблицы вычисляется по формуле:

 (1.12)
(1.12)
Процедуру преобразования элементов симплекс-таблицы по указанному алгоритму при выполнении замены 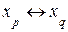 называют симплекс-преобразованием. Все этапы решения задачи линейного программирования состоят из соответствующих симплекс-преобразований. Любое симплекс-преобразование характеризуется выбором соответствующего разрешающего элемента, не равного нулю и не являющегося коэффициентом целевой функции или свободным членом. Для скорейшего приближения задачи линейного программирования следует руководствоваться определенными правилами выбора разрешающего элемента.
называют симплекс-преобразованием. Все этапы решения задачи линейного программирования состоят из соответствующих симплекс-преобразований. Любое симплекс-преобразование характеризуется выбором соответствующего разрешающего элемента, не равного нулю и не являющегося коэффициентом целевой функции или свободным членом. Для скорейшего приближения задачи линейного программирования следует руководствоваться определенными правилами выбора разрешающего элемента.
6. Правило выбора разрешающего элемента для нахождения опорного решения
Предположим, что в некотором состоянии симплекс-таблицы хотя бы в одной из её строк имеется отрицательный свободный член. Следовательно, это состояние симплекс-таблице не является (согласно определению) полуприведенным. Требуется найти симплекс-преобразование, в результате которого будет получена приведенная симплекс-таблица или, согласно теореме 1, опорное решение. Как отмечалось выше, любое симплекс-преобразование характеризуется выбор его разрешающего элемента. Алгоритм такого выбора следующий.
В строке симплекс-таблицы, содержащей отрицательный свободный член, возьмем любой положительный элемент. Столбец, в котором находится этот элемент, примем за разрешающий. Для выбора в разрешающем столбце разрешающего элемента рассмотрим все отрицательные отношения свободных членов симплекс-таблицы (исключая свободный член 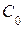 целевой функции) к элементам разрешающего столбца. Тот элемент разрешающего столбца, для которого это отношение является наибольшим, следует взять в качестве разрешающего элемента.
целевой функции) к элементам разрешающего столбца. Тот элемент разрешающего столбца, для которого это отношение является наибольшим, следует взять в качестве разрешающего элемента.
7. Правило выбора разрешающего элемента для нахождения оптимального решения
Предположим, что симплекс-таблица является полуприведенной. Укажем алгоритм перехода к её приведенному состоянию, которому согласно теореме 2, соответствует искомое оптимальное решение задачи линейного программирования.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 520; Нарушение авторских прав?; Мы поможем в написании вашей работы!