Линейная и круговая свертки

ЛИНЕЙНЫЕ ЦИФРОВЫЕ СИСТЕМЫ

2.1.1. Линейная свертка. Обработка сигналов в линейных цифровых системах осуществляется по алгоритмам, являющимися дискретными аналогами интеграла свертки [1]

или при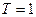

(2.1)

где – выходной отклик, состоящий из отсчетов; 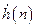– импульсная характеристика линейной системы, состоящая из 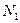отсчетов; – отсчеты входного сигнала, количество которых равно 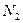; величина ; 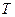– период дискретизации.

Выражение (2.1) для простоты обозначения переменных часто записывают в форме

.

Другая форма записи выражения (2.1) имеет вид

,

или в виде

, (2.2)

где знак – обозначает операцию свертки.

Линейная свертка (2.1) или (2.2) также носит название апериодической и описывает работу линейных цифровых систем, работающих в режиме «скользящее» окно [1].

Пример 2. Пусть имеем последовательность 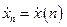, состоящую из отсчетов в виде

. (2.3)

Пусть также имеется последовательность 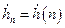, состоящая из 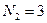отсчетов в виде

.

Количество выходных отсчетов будет равно величине

.

Используя выражение (2.1) вычислим линейную свертку для соответствующих временных значений.

2.1.2. Круговая свертка. Часто та или иная последовательность отсчетов носит периодический характер с периодом 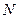отсчетов. Например, отсчеты в частотной области выборочного спектра входного сигнала с периодом 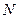отсчетов, отсчеты в частотной области амплитудно-частотной характеристики (АЧХ) цифровой линейной цепи с периодом 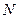отсчетов. Очевидно, что выходной результирующий спектр, являющийся результатом произведения соответствующих отсчетов спектра входного сигнала и АЧХ друг на друга, тоже будет периодическим с периодом 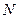отсчетов.

Обратное преобразование Фурье выходного спектра с периодом 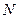отсчетов также будет периодическим во временной области с периодом отсчетов.

Выражение во временной области для круговой свертки периодического выходного результирующего спектра с периодом 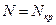отсчетов будет иметь вид

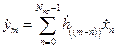. (2.5)

Выражение (2.4) может быть записано в виде

. (2.6)

В выражениях (2.5) и (2.6) индексы в круглых скобках при значениях 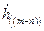и обозначают, что они берутся по модулю отсчетов.

Например, если модуль , то

Количество отсчетов во времени круговой свертки, как видно из (2.5), равно количеству отсчетов в частотной области, в то время как количество отсчетов линейной свертки в (2.1), зависит от количества отсчетов используемых при расчетах реализаций (импульсной характеристики и входного процесса), ее образующих, минус один отсчет.

Пример 3. Пусть имеем последовательность 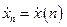, состоящую из отсчетов в виде (2.3)

.

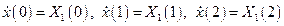Пусть также имеется последовательность , состоящая из отсчетов в виде

.

Количество различных выходных отсчетов для круговой свертки будет равно величине .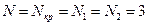

В выражении (2.7) видно, что выходные отсчеты для круговой свертки повторяются с периодом .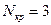

2.1.3. Пример 4. Вычислить и изобразить на рисунке линейную и круговую свертки для двух конечных последовательностей длительностью по три отсчета каждая. Здесь полагается, что величина периода дискретизации .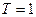

Первая конечная последовательность

Вторая конечная последовательность

Линейная свертка. Подставляя в (2.4) численные значения получаем следующие результаты

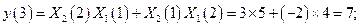
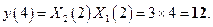
Следовательно, отсчеты линейной свертки имеют вид

.

На рис. 1 изображены отсчеты линейной свертки.

Рис. 1. Отсчеты линейной свертки

Круговая свертка. Подставляя в (2.7) численные значения получаем следующие результаты.

Далее процесс расчета повторяется.

Следовательно, отсчеты круговой свертки имеют вид

и они периодически повторяются с периодом .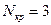

На рис. 2 изображены отсчеты круговой свертки.

Рис. 2. Отсчеты круговой свертки

Видно, что отсчет линейной свертки численно совпадает с отсчетом круговой свертки. Это используется при вычислении спектров с использованием алгоритмов быстрого расчета коэффициентов Фурье.

Аналогичным образом решаются все задачи в п.10.1.4. в [2].

Дата добавления: 2014-12-24