Расчет параметров цифрового частотного дискриминатора

Определение характеристик цифровых линейных цепей по их структурным схемам

Очевидно, что определение характеристик цифровых линейных цепей по их структурным схемам тоже относится к обратным задачам, относительно случая реализации структурной схемы по параметрам уравнений.

Определение характеристик цифровых линейных цепей по их структурным схемам осуществляется за ряд этапов.

Первый этап заключается в определении вида анализируемой структурной схемы, которые могут быть рекурсивными, нерекурсивными и рекурсивными с прямыми связями.

Второй этап заключается в отыскании передаточной функции на Z -плоскости цифровой линейной цепи.

Третий этап осуществляет переход от передаточной функции на Z -плоскости к разностному уравнению, описывающему работу цифровой линейной цепи последовательно во времени.

Четвертый этап посвящен расчету АЧХ линейной цифровой цепи по ее передаточной функции на Z -плоскости.

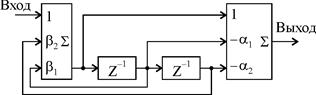
Пример 10. По структурной схеме, которая изображена на рис. 16, записать выражение для передаточной функции на Z -плоскости, разностное уравнение и рассчитать АЧХ данной цифровой линейной системы (цифрового фильтра).

Рис. 16. Структурная схема цифровой биквадратной ячейки с прямыми и обратными связями

Передаточная функция на Z -плоскости цифровой биквадратной ячейки с прямыми и обратными связями описывается выражением (2.13).

Подставляя в выражение (2.13) весовые коэффициенты, величины которых изображены на входах сумматоров, и с учетом связи весовых коэффициентов с величинами 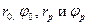передаточная функция примет вид

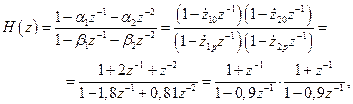(2.40)

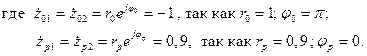
Разностное уравнение получается следующим образом.

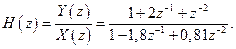
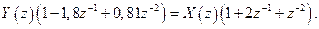
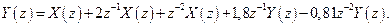
Подвергая обратному Z -преобразованию последнее выражение, получим разностное уравнение в виде

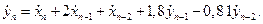
Рассчитаем АЧХ рассмотренной цифровой линейной цепи. Видно, что в уравнении (2.40) имеется произведение двух одинаковых сомножителей в числителе и в знаменателе для заданных величин весовых коэффициентов, т.е.

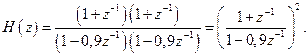
АЧХ числителя описывается выражением (2.18), знаменатель – выражением (2.33). Тогда в ненормированном виде АЧХ записывается в виде

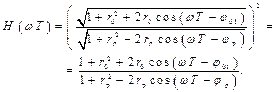(2.41)

Подставляя значения величин 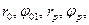последнее выражение примет вид

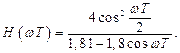
В нормированном виде выражение (2.41) запишется следующим образом

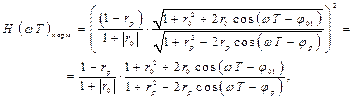
откуда, подставляя значения величин 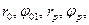получим

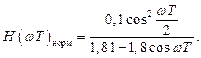(2.42)

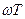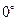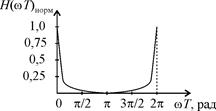
Изменяя независимую переменную в диапазоне от 0 до 2 p (рад) или от до 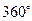в выражении (2.42), получим АЧХ цифровой линейной цепи, которая изображена на рис. 17.

Рис. 17. Рассчитанная нормированная АЧХ цифровой линейной цепи

Аналогичным образом решаются все задачи в п.10.2.3. в [2].

Основной особенностью цифрового частотного дискриминатора (ЦЧД), реализующего обработку бинарно-квантованных сигналов в режиме работы «скользящее» окно, является возможность достаточно простого управления крутизной дискриминационной характеристики (ДХ) [1].

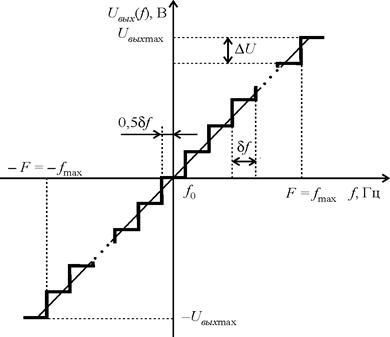
На рис. 18 представлен пример ДХ ЦЧД.

Рис. 18. Идеальная (прямая) и реальная (ступенчатая) дискриминационные характеристики

Расчет параметров цифрового частотного дискриминатора (ЦЧД), осуществляется по следующим выражениям.

Крутизна дискриминационной характеристики (ДХ) 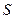(В/Гц) определяется из следующего выражения

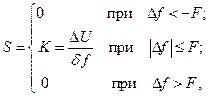(3.1)

где 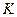(В/Гц) – коэффициент, характеризующий крутизну ДХ; 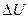(В) – величина напряжения, приходящаяся на один разряд; 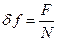(Гц) – вес одного разряда; 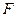(Гц) – половина ширины раскрыва ДХ ЦЧД, определяемая емкостью реверсивного счетчика; 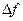(Гц) – разность частот между частотой входного сигнала 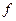и опорной частотой; 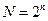– величина, определяющая количество состояний реверсивного счетчика; – величина, определяющая количество разрядов реверсивного счетчика.

Максимальное напряжение 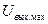(В) на выходе ДХ ЦЧД определяется в соответствии с выражением

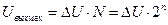(В),

откуда

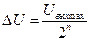(В). (3.2)

Как известно, точное значение той или иной частоты соответствует середине интервала 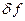(Гц). Очевидно, что нахождение частоты в любой точке частотной оси, соответствующей весу того или иного разряда, равновероятно. Отсюда, выражение для плотности распределения вероятностей ошибки определения частоты внутри одного разряда, будет

.

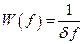Учитывая то обстоятельство, что математическое ожидание равно нулю, а критерием точности является среднеквадратическая величина

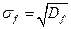(Гц),

где 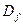– дисперсия частоты, то имеем

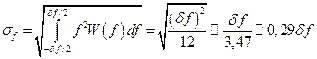(Гц). (3.3)

Относительная погрешность измерения

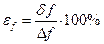. (3.4)

Относительная погрешность 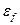(%) будет минимальна при 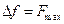(Гц) и будет увеличивается по мере приближения входной частоты к опорной.

Абсолютное значение погрешности измерения 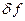(Гц) зависит от диапазона анализа 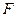(Гц) и числа разрядов .

Максимальная величина диапазона (раскрыва ДХ) будет

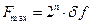(Гц),

откуда

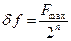(Гц). (3.5)

Пример 11. Рассчитать крутизну ДХ 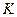(В/Гц) ЦЧД, определить вес одного разряда 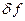(Гц), среднеквадратическую погрешность 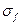(Гц), и относительную погрешность 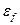(%) для двух значений максимальной частоты линейного участка ДХ 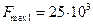(Гц) и 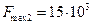(Гц). Полагаем, что число разрядов реверсивного счетчика 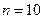, а максимальное выходное напряжение 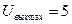(В).

Определим количество состояний реверсивного счетчика

.

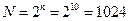Определим, используя (3.2), величину

.

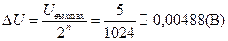Определим, используя (3.5), величины веса одного разряда 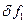и

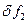
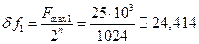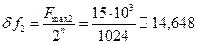(Гц);

(Гц).

Крутизна ДХ 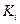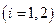с учетом (3.1) будет

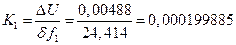(В/Гц)=199,885(мкВ/Гц);

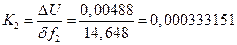(В/Гц)=333,151(мкВ/Гц).

С учетом (3.3), величины среднеквадратической погреш-ности 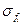будут

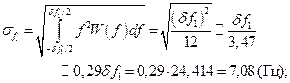
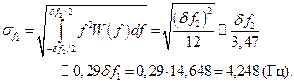
Относительная 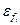погрешность, с учетом (3.4), будет

;

.

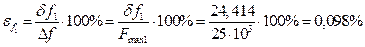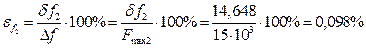Аналогичным образом решаются все задачи в п.10.1.9. в [2].

Дата добавления: 2014-12-24