Пуассоновские потоки

ДЛЯ АНАЛИЗА ЦИФРОВЫХ УСТРОЙСТВ

ПРИМЕНЕИЕ АППАРАТА ЦЕПЕЙ МАРКОВА

В том случае, когда обработке подвергаются процессы, представленные в бинарно-квантованной форме, для анализа эффективности разработанных цифровых устройств, применяют математический аппарат цепей Маркова [3]. Аппарат цепей Маркова позволяет описывать состояния, в которых находятся те или иные цифровые узлы.

Одним из видов марковских процессов являются разрывные процессы, которые представляют собой пуассоновские потоки событий [3]. Эти процессы лежат в основе теории надежности и теории массового обслуживания и имеют непосредственное отношение к описанию работы различных радиотехнических систем.

Пусть система имеет конечное число состояний . Под воздействием пуассоновских потоков из любого состояния 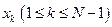возможен переход в соседние состояния и 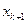. Переход из состояния 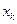в состояние 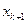означает, например, поступление на суммирующий вход реверсивного счетчика (РС) единицы, а переход из состояния 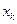в состояние означает поступление единицы на его вычитающий вход. При этом полагается, что интенсивности появления единиц на входах РС представляют собой стационарные пуассоновские процессы.

Обозначим интенсивность потока, переводящего систему из состояния 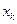в состояние 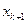, через 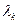, а интенсивность потока, переводящего систему из состояния 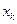в состояние , через .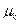

На рис. 22 изображен процесс, развивающейся в такой системе, в виде графа состояний. Здесь учтено, что в том случае, когда РС заполнен, то добавление по суммирующему входу единицы переводит все его разряды в нулевое состояние, а в случае, когда РС находится в нулевом состоянии, то появление на его вычитающем входе единицы переводит все его разряды в единичное состояние.

Рис. 22. Процесс перехода из состояния в состояние в виде графа в реверсивном счетчике

В те моменты времени, когда по обоим входам РС не поступают сигналы или когда сигналы поступают по обоим входам одновременно, его состояние не изменяется и обозначается через .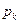

В работе [3] приводится вывод выражения, позволяющего определить для стационарного случая финальную вероятность в соответствии с выражением

.

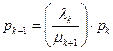Последнее выражение является рекуррентным, т.е. оно позволяет выразить значение вероятности 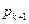через предыдущие значения в виде

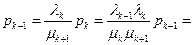
(5.1)

Вероятность , через которую выражаются вероятности всех остальных состояний, находится из условия нормировки [3]

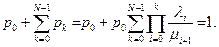
Из последнего выражения следует, что

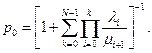
Видно, что по заданным интенсивностям 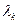и 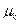определяются финальные вероятности 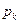при заданной конечной величине 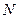. Отметим, что для РС вероятность нахождения первого разряда в одном из двух положений (нуль или единица) в момент включения будет .

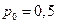Пример 15. На входы РС с 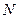состояниями поступают по двум входам в виде пуассоновского потока последовательности импульсов. Вероятность нахождения первого разряда счетчика в одном из состояний 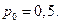Вероятность перехода из состояния, в котором счетчик находится в 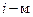испытании в состояние на единицу большее в 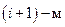испытании равно 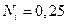, а на единицу меньше равно 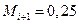. Определить вероятность 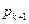нахождения реверсивного счетчика в состоянии 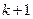, где 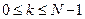для величин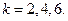

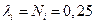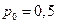Очевидно, что следует воспользоваться выражением (5.1). Из него видно, что , а величина . Также видно, что . Тогда величины 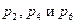будут

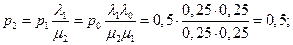
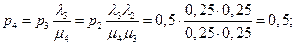
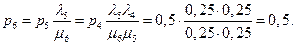
Следовательно, независимо от числа испытаний 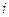система находится в финитном состоянии, которое зависит только от статистических характеристик процессов на ее входах.

Аналогичным образом решаются все задачи в п.10.2.7. в [2].

Дата добавления: 2014-12-24