Вычисление финальных вероятностей

Как показано в [3], вычисление финальных вероятностей нахождения цифровой системы в том или ином состоянии достаточно просто реализуется при известном начальном распределении и заданной матрице перехода.

В этом случае, для описания цифровой системы используется матрица вероятности перехода системы 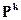из состояния в состояние, величины элементов которой зависят от моментов времени 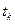. Когда отсутствует зависимость величин вероятностей перехода системы из одного состояния в другое состояние от момента времени 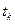, т.е. 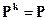, то такие цепи Маркова называются однородными.

Основной особенностью однородных матриц вероятностей перехода 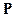является то, что сумма вероятностей в каждой ее строке равна единице. Это объясняется тем, что если количество строк матрицы соответствует количеству состояний, то элементы каждой строки описывают вероятность пребывания соответствующего элемента цифровой системы в том или ином состоянии.

В том случае, когда в рассматриваемой цифровой системе отсутствуют поглощающие состояния, т.е. состояния, при достижении которых (или которого) система перестает изменяться под воздействием соответствующих сигналов, то такие системы описываются цепями Маркова, называемыми эргодическими [3].

Однако полной характеристикой системы, описываемой однородными эргодическими цепями Маркова, является ее описание при помощи финальной матрицы вероятностей , которая определяется в виде

,

где 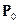– вектор-строка начальных состояний цифровой системы; – количество шагов, за которое система из первоначального состояния, описываемого 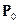, перейдет в финальное состояние, описываемое матрицей .

Как показано в [3], после определенного числа шагов финальное состояние системы полностью определяется величиной 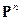, т.е.

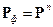. (5.2)

Выражение (5.2) показывает, что цифровая система через определенное число шагов «забывает» свое первоначальное состояние 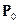и ее финальное состояние полностью зависит от элементов матрицы вероятностей перехода .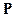

Пример 16. Рассмотрим, на числовом примере, как изменяются матрицы перехода и безусловные вероятности состояний с ростом числа в выражении (5.2) [3].

Положим, что нужно определить финальные вероятности цифровой системы.

Для этого воспользуемся соотношением (5.2).

Пусть матрица вероятностей перехода 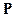из состояния в состояние задается в виде

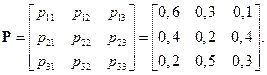
Последовательно возводя эту матрицу во вторую, третью, четвертую и пятую степени, получаем

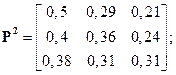
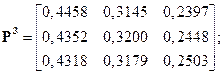
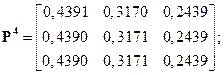
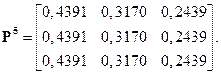
Видно, что после пятой итерации матрица перехода вырождается в матрицу, полностью определяемую матрицей-строкой.

Согласно теореме Маркова [3], финальные вероятности для этого примера равны

,

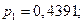
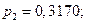
откуда матрица финальных вероятностей будет

.

Видно, что сумма этих вероятностей равна единице.

Количество шагов перехода цифровой системы из первоначального состояния в финальное состояние равно

.

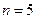Аналогичным образом решается задача в п.10.2.8. в [2].

ЗАКЛЮЧЕНИЕ

В данном учебном пособии приводятся теоретические сведения и примеры решения типовых задач, которые наиболее часто встречаются как на практических занятиях, так и при выполнении контрольных работ. Решения всех задач основано на изложенной соответствующей методике. Тем не менее, в некоторых случаях следует либо применять известные методы, позволяющие упрощать полученные уравнения и сводить их к известным решениям, либо требуют, в случае необходимости, обращения к работе [1] для более полной предварительной проработки необходимого теоретического материала. Следует отметить, что задачи в [2] составлены так, чтобы их решения сводились к решению либо простейших, либо они отличаются друг от друга только числовыми данными.

Дата добавления: 2014-12-24